Nessa categoria desenvolvemos o conteúdo que envolve a teoria básica e aplicações da transformada de Laplace. Além disso, trazemos soluções de equações que modelam fenômenos físicos importantes como as EDOs que governam circuitos elétricos e sistemas mecânicos, além de EDPs que controlam dissipação de calor, ondas e diversos outros fenômenos naturais.
A transformada de Laplace é uma transformada integral talvez perdendo apenas para a transformada de Fourier em sua utilidade na resolução de problemas físicos.
A transformada de Laplace é particularmente útil na resolução de equações diferenciais ordinárias lineares , como as que surgem na análise de circuitos eletrônicos.
Se f(t) é uma função definida para todo t \geq 0, sua Transformada de Laplace é uma função na variável s, chamada de F(s) e denotada por \mathscr{L} (f) é dada pela integral F(s) = \mathscr{L} (f) = \int_{0}^{\infty}{e^{-st}f(t)dt} = \lim_{T \rightarrow \infty}{\int_{0}^{T}{e^{-st}f(t)dt}}. A função dada f(t) é denominada de transformada inversa de F(s) e é denotada por \mathscr{L}^{-1} (F), ou seja, f(t) = \mathscr{L}^{-1} (F(s)).
O método da Transformada de Laplace é uma ferramenta muito poderosa na solução de EDO’s lineares e PVI’s correspondentes que pode ser resumido em três passos:
Esta comutação do cálculo para a álgebra é chamada de Cálculo Operacional.
| Abaixo temos os tópicos sobre a TRANSFORMADA DE LAPLACE abordados em sequência. Basta clicar nos links em azul para ser redirecionado ao conteúdo. Em cada um deles existe uma vídeo-aula disponível |
1 – A Transformada de Laplace
1.1 – Transformada de Laplace – Definição, exemplos e propriedades
1.1.1 – Transformada de Laplace | 1ª Lista de Exercícios Resolvidos
1.1.2 – Transformada de Laplace | 2ª Lista de Exercícios Resolvidos
1.1.3 – Transformada de Laplace | 3ª Lista de Exercícios Resolvidos
1.1.4 – Transformada de Laplace | 4ª Lista de Exercícios Resolvidos
1.1.5 – Transformada de Laplace | 5ª Lista de Exercícios Resolvidos
1.1.6 – Transformada de Laplace | 6ª Lista de Exercícios Resolvidos
1.2 – A Transformada de Laplace Inversa
1.2.1 – Transformada de Laplace Inversa | Lista de Exercícios Resolvidos
1.3 – Tabela Completa de Transformadas de Laplace
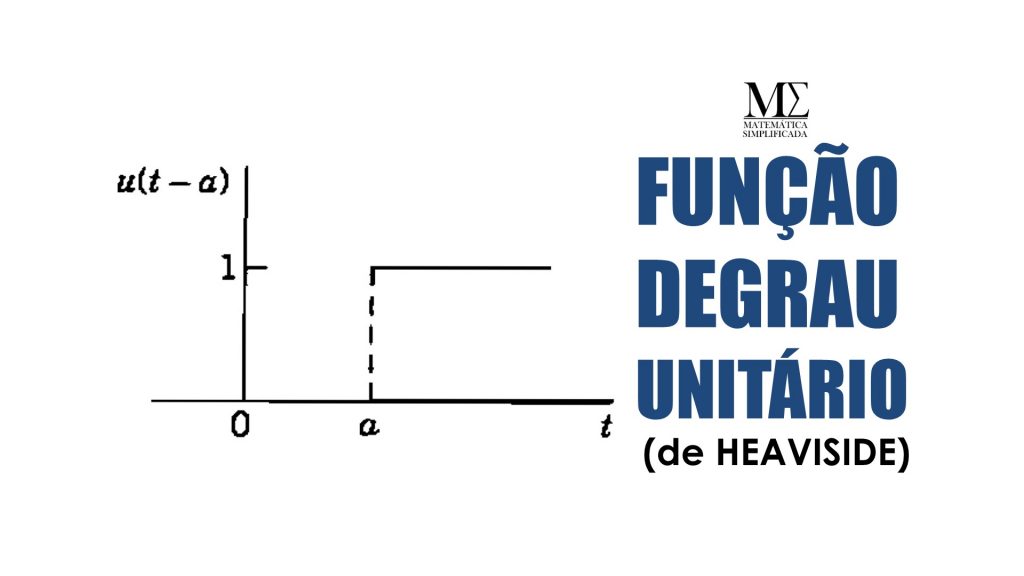
1.4 – A Função Degrau ou Função de Heaviside
1.4.1 – Função Degrau Unitário | 1ª Lista de Exercícios Resolvidos
1.4.2 – Função Degrau Unitário | 2ª Lista de Exercícios Resolvidos
1.5.1 – Lista de Exercícios sobre Delta de Dirac
1.6.1 – Equação Integral de Volterra
1.6.2 – A Convolução – Lista de Exercícios Resolvidos
1.7 – Propriedade da Derivada de F(s)
1.8 – Transformada de Laplace de Uma Função Periódica
2 – Resolvendo E.D.O’s Lineares Via Transformada de Laplace
2.1 – Solucionando Equações Diferenciais Ordinárias via Transformada de Laplace
2.1.1 – Resolvendo EDO’s por Laplace | 1ª Lista de Exercícios Resolvidos
2.1.2 – Resolvendo EDO’s por Laplace | 2ª Lista de Exercícios Resolvidos
2.1.3 – Resolvendo EDO’s por Laplace | 3ª Lista de Exercícios Resolvidos
2.1.4 – Resolvendo EDO’s por Laplace | 4ª Lista de Exercícios Resolvidos
2.1.5 – Resolvendo EDO’s por Laplace | 5ª Lista de Exercícios Resolvidos
2.1.6 – Resolvendo EDO’s por Laplace | 6ª Lista de Exercícios Resolvidos
2.1.7 – Resolvendo EDO’s por Laplace | 7ª Lista de Exercícios Resolvidos
2.1.8 – Resolvendo EDO’s por Laplace | 8ª Lista de Exercícios Resolvidos
2.1.9 – Resolvendo EDO’s por Laplace | 9ª Lista de Exercícios Resolvidos
2.1.10 – Resolvendo EDO’s por Laplace | 10ª Lista de Exercícios Resolvidos
2.1.11 – Resolvendo EDO’s por Laplace | 11ª Lista de Exercícios Resolvidos
2.1.12 – Resolvendo EDO’s por Laplace | 12ª Lista de Exercícios Resolvidos
2.1.13 – Resolvendo EDO’s por Laplace | 13ª Lista de Exercícios Resolvidos
2.1.14 – Resolvendo EDO’s por Laplace | 14ª Lista de Exercícios Resolvidos
5.9.15 – Resolvendo EDOs por Laplace | 15ª Lista de Exercícios Resolvidos
3 – Aplicações da Transformada de Laplace
3.1 – Circuitos Elétricos em Série
3.2 – Equação Integral de Volterra | Convolução e Transformada de Laplace
3.3 – A Solução da Equação da Onda Unidimensional Usando a Transformada de Laplace
Bibliografia
O site Matemática Simplificada foi criado com o intuito de auxiliar no estudo e no aprendizado da matemática, desde os tópicos mais básicos até os conteúdos das disciplinas usualmente tratadas nas graduações que envolvem ciências exatas.
Grande parte do conteúdo aqui apresentado é retirado de livros usados como livros-texto nos cursos de graduação e selecionado à partir das ementas destes mesmos cursos.
Abaixo seguem os títulos usados como base para os nossos artigos desta disciplina.
GUIDORIZZI, H.L. Um curso de cálculo: Vol 1, 2,3 e 4. Rio de Janeiro: LTC, 2001.
ÁVILA, G. Variáveis Complexas e Aplicações, LTC, Rio de Janeiro,1990
BRAUN, M. Equações Diferenciais e suas Aplicações, Editora Campus, Rio de Janeiro, 1979.
THOMAS, G. B. Cálculo, Editora Pearson Education, São Paulo, 2002.
ZILL, D. G. Equações Diferenciais com Aplicações em Modelagem, Editora Pioneira –
Thomson Learning, São Paulo, 2003.
SPIEGEL, M. R. Análise de Fourier, McGraw-Hill, São Paulo, 1976.
KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.
Existem algumas funções que são de considerável interesse nas mais diversas áreas da ciência. Algumas delas, principalmente, são importantes nas soluções de equações diferenciais atreladas a modelagens de fenômenos descontínuos, como a FUNÇÃO DEGRAU UNITÁRIO ou FUNÇÃO DE HEAVISIDE. A função de Heaviside ou função degrau unitário, desenvolvida pelo matemático e engenheiro eletricista Oliver Heaviside é simples de ser definida, […]
Nesse artigo trabalhamos com foco na inversa da Transformada de Laplace, frações parciais e a translação, por exemplos e exercícios.
Neste artigo investigamos o Delta de Dirac. Da definição às aplicações da Transformada de Laplace na solução de Equações Diferenciais.
