A Transformada de Laplace de uma Função Periódica

O método da Transformada de Laplace é uma ferramenta muito poderosa na solução de Equações Diferenciais, Ordinárias e Parciais, que pode ser resumido em três passos:

1. A Equação Diferencial dada é transformada em uma equação algébrica.
2. Esta equação é solucionada por manipulações algébricas.
3.  A solução obtida no item 2 é transformada de volta obtendo a solução do problema original dado.

Se f(t) é uma função definida para todo t \geq 0, sua Transformada de Laplace é uma função na variável s, chamada de F(s) e denotada por \mathscr{L} (f) é dada pela integral F(s) = \mathscr{L} (f) = \int_{0}^{\infty}{e^{-st}f(t)dt} = \lim_{T \rightarrow \infty}{\int_{0}^{T}{e^{-st}f(t)dt}}. A função dada f(t) é denominada de transformada inversa de F(s) e é denotada por \mathscr{L}^{-1} (F), ou seja, f(t) = \mathscr{L}^{-1} (F(s)).

Leia Mais: Transformada de Laplace | Das Definições Básicas à Função Delta

O que são Funções Periódicas?

Em diversos casos é importante tratar de problemas de natureza periódica, até por isso é importante estabelecer a Transformada de Laplace para este tipo de função.

Uma função f:\mathbb{R} \rightarrow \mathbb{R} é chamada de função periódica de período T se $$f(x+T) = f(x)$$ para todo x.

O gráfico de uma função periódica é obtido pela repetição periódica do seu gráfico em qualquer intervalo de tamanho T.

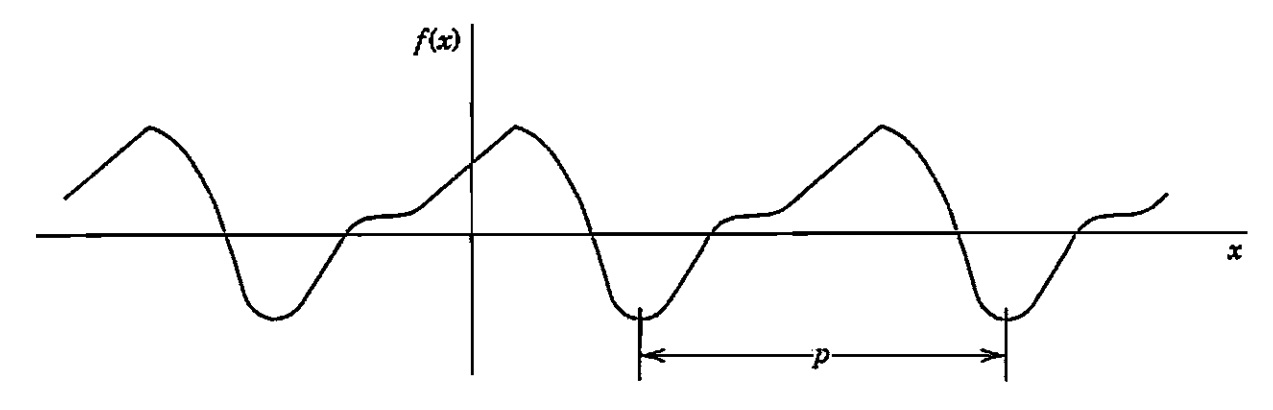
São exemplos imediatos de funções periódicas:

• As funções \sin{x} e \cos{x} são periódicas e com período igual a 2 \pi.
• A função \tan{x} é periódica e com período igual a \pi.

PROPRIEDADES DAS FUNÇÕES PERIÓDICAS:

Seja f(x) uma função real periódica com período T. Então, podemos estabelecer as seguintes propriedades:

Para todo n \in \mathbb{Z}, temos que $$f(x+nT) = f(x).$$
Se f(x) e g(x) possuem período T, então $$h(x) = \alpha f(x) + \beta g(x); \;\;\;\;\;\alpha , \beta \in \mathbb{R}.$$

Leia Mais: O Que São Funções Periódicas? Definição e Exemplos.

A Transformada de Laplace de Uma Função Periódica

Se uma função f periódica tem período T, T>0, então sua transformada de Laplace pode ser obtida por uma integração sobre o intervalo [0, T).

TEOREMA (Transformada de uma Função Periódica):

Seja f(t) contínua por partes em [0, \infty ) de ordem exponencial. Se f(t) for periódica de período T, então $$\mathscr{L} [f(t)] = \frac{1}{1- e^{-sT}} \int\limits^{T}_{0}{e^{-st} f(t)dt} .$$

EXEMPLO:

Encontre a transformada de Laplace da função periódica dada por:

$$f(t)=\left\{\begin{array}{rl}
t; & 0 \leq t <1 \\
\\
0; & 1 \leq t < 2 \end{array}\right. ; \;\;\; f(t+2) = f(t).$$

Como T = 2, usamos o teorema acima e a integração por partes para obter

$$\mathscr{L} [f(t)] = \frac{1}{1- e^{-2s}} \int\limits^{2}_{0}{e^{-st} f(t)dt} = $$  $$ = \frac{1}{1- e^{-2s}} \left[  \int\limits^{1}_{0}{t e^{-st} dt} +  \int\limits^{2}_{1}{0 e^{-st} dt} \right] = \frac{1}{1- e^{-2s}} \int\limits^{1}_{0}{t e^{-st} dt} = $$ $$= \frac{1}{1- e^{-2s}} \left[  – \frac{e^{-s}}{s} + \frac{1- e^{-s}}{s^2}   \right] = \frac{1 – (s+1) e^{-s}}{s^2 (1- e^{-2s})}.$$

EXEMPLO

A função f(t) = cos( \omega t) é periódica, com período T = 2 \pi / \omega .

Assim, $$\mathscr{L} [cos(t)] = \frac{1}{1- e^{-2 \pi s / \omega}} \int\limits^{2 \pi / \omega}_{0}{e^{-st} cost(t)dt} = $$ $$ = \frac{1}{1- e^{-2 \pi s / \omega}} \left[ \frac{\omega \,\mathrm{sin}\left( t\,\omega \right) -s\,\mathrm{cos}\left( t\, \omega \right) }{{e}^{s\,t}\,{\omega}^{2}+{s}^{2}\,{e}^{s\,t}} \right]^{2 \pi / \omega}_{0} = $$ $$ = \frac{1}{1- e^{-2 \pi s / \omega}} \left[  \frac{{e}^{-\frac{2\,\pi \,s}{w}}\,\left( s\,{e}^{\frac{2\,\pi \,s}{w}}-s\right) }{{w}^{2}+{s}^{2}}  \right] = $$ $$ = \frac{1}{1- e^{-2 \pi s / \omega}} \left[ \frac{s – s e^{\frac{-2 \pi s}{\omega}}}{s^2 + \omega ^2} \right] = \frac{s}{s^2 + \omega ^2} .$$

Leia Mais:

• A Convolução e a Transformada de Laplace
• O Delta de Dirac | Da definição à solução de Equações Diferenciais
• Função de Heaviside ou Degrau Unitário
• Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos
• Transformada de Fourier | Uma Introdução aos Conceitos Básicos
• Equações Diferenciais | Introdução aos Conceitos Básicos