Transformada de Laplace | 4ª Lista de Exercícios Resolvidos

Se f(t) é uma função definida para todo t \geq 0, sua Transformada de Laplace é uma função na variável s, chamada de F(s) e denotada por \mathscr{L} (f) é dada pela integral F(s) = \mathscr{L} (f) = \int_{0}^{\infty}{e^{-st}f(t)dt} = \lim_{T \rightarrow \infty}{\int_{0}^{T}{e^{-st}f(t)dt}}. A função dada f(t) é denominada de transformada inversa de F(s) e é denotada por \mathscr{L}^{-1} (F), ou seja, f(t) = \mathscr{L}^{-1} (F(s)).

4ª Lista de Exercícios Resolvidos sobre Transformada de Laplace

Na solução dos exercícios abaixo usamos as integrais tabeladas dadas abaixo. Para uma tabela mais completa sobre a Transformada de Laplace, confira este nosso artigo.

1) Encontre a Transformada da função dada pelo gráfico abaixo. (Dica: escreva a função em termos da função degrau)

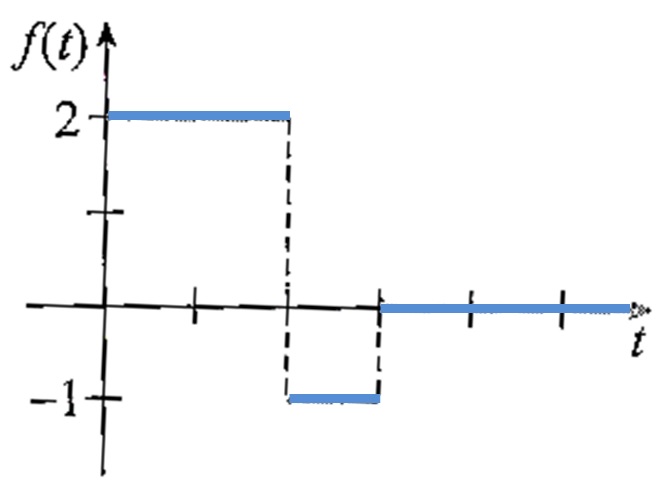
SOLUÇÃO: Com a ajuda da função degrau unitário, podemos escrever $$f(t) = 2 – 3 u(t-2) + u(t – 3).$$ Usando a linearidade e a transformada de Laplace da função degrau encontramos $$ \mathscr{L}\{f(t)\} = \mathscr{L}\{2 – 3 u(t-2) + u(t – 3)\} = $$ $$ =  \mathscr{L}\{2\} – 3 \mathscr{L}\{u(t-2) \} + \mathscr{L}\{u(t – 3)\} = $$ $$ = \frac{2}{s} – 3 \frac{e^{-2s} }{s} + \frac{e^{-3s} }{s} .$$

2) Seja g(t) = \int_{0}^{t}{e^{ \tau} sen\left( t - \tau \right) d \tau}. Calcule \mathscr{L}\{g(t)\}. (dica: use a convolução)

SOLUÇÃO: Como f(t) = e^t e g(t) = sen(t) , o teorema da convolução diz que a Transformada de Laplace da convolução de f e g é o produto de suas transformadas. Logo, $$ \mathscr{L}\left\{ \int_{0}^{t}{e^{ \tau} sen\left( t – \tau \right) d \tau} \right\} = \mathscr{L}\left\{ e^{t} sen\left( t \right) \right\} = $$ $$ = \mathscr{L}\left\{ e^{t} \right\} \times \mathscr{L}\left\{ sen\left( t \right) \right\} = \frac{1}{s-1} \times \frac{1}{s^2+1} = \frac{1}{(s-1)(s^2+1)} .$$

3) Determine

a) \mathscr{L}\{t^2 u(t-1)\} =

SOLUÇÃO: Neste caso, para usar o Teorema da Translação termos que colocar a função t^2 em termos da função t-1 . Observe que $$t^2 = (t^2 – 2t +1 ) +2t -1 = (t-1)^2 +2t -2 +2 -1 = (t-1)^2 + 2(t-1)+1.$$ Logo, $$ t^2 u(t-1) = [ (t-1)^2 + 2(t-1)+ 1]u(t-1) = $$  $$= (t-1)^2 u(t-1) + 2(t-1) u(t-1)+ u(t-1).$$ Portanto, $$\mathscr{L}\{t^2 u(t-1)\} = \mathscr{L}\{(t-1)^2 u(t-1) \} + 2 \mathscr{L}\{(t-1) u(t-1) \} + \mathscr{L}\{u(t-1) \} = $$ $$ = e^{-s} \left( \frac{2}{s^3} + \frac{2}{s^2} + \frac{1}{s} \right).$$

b) \mathscr{L}\{[cos(t)] u(t-\pi)\}=

SOLUÇÃO: Novamente precisamos fazer um ajuste na função cos(t) para poder usar o Teorema da Translação. Observe que pela propriedade cos(t -\pi) = - cos(t) teremos $$\mathscr{L}\{[cos(t)] u(t-\pi)\} = \mathscr{L}\{[-cos(t- \pi)] u(t-\pi)\} = – e^{-\pi s} \frac{s}{s^2 +1}.$$

c) \mathscr{L}\{\delta{ (t-1) } - \delta{ (t-3) }\}=

SOLUÇÃO: \mathscr{L}\{\delta{ (t-1) } - \delta{ (t-3) }\}= \mathscr{L}\{\delta{ (t-1) } \} - \mathscr{L}\{\delta{ (t-3) }\}  = e^{-s} - e^{-3s}.

d) \mathscr{L}^{-1}\left\{ \dfrac{e^{-2s}}{s^2} \right\}=

SOLUÇÃO: Para usar a propriedade da translação, expressamos primeiro e^{- 2s} / s^2 como o produto e^{- 2s} F(s) . Para esta finalidade, colocamos F(s) = 1/ s^2 . Logo $$ f(t) = \mathscr{L}^{-1}\left\{ \frac{1}{s^2} \right\} = t$$ e observando que a = 2, usamos a propriedade da translação e encontramos $$ \mathscr{L}^{-1}\left\{ \frac{e^{-2s}}{s^2} \right\}= (t-2)u(t-2) . $$

e) \mathscr{L}^{-1}\left\{ \dfrac{1}{(s^2+1)^2} \right\}=

SOLUÇÃO: Neste caso escreveremos $$\frac{1}{(s^2+1)^2} = \left( \frac{1}{(s^2+1)} \right) \times \left( \frac{1}{(s^2+1)} \right).$$ Como \mathscr{L}^{-1}\left\{ \dfrac{1}{s^2+1} \right\}= sen(t) , então $$ \mathscr{L}^{-1}\left\{ \frac{1}{(s^2+1)^2} \right\}= sen(t) \ast sen(t) = $$ $$ = \int_{0}^{t}{sen (\tau) sen (t – \tau) d \tau} = \frac{sen(t) – tcos(t}{2} .$$

4) Escreva a função abaixo em termos da função degrau e calcule sua transformada de Laplace: $$f(t) = \left\{ \begin{array}{lll} 3 &; & t <2 \\ 1 &; & 2< t <5 \\ t &; & 5 < t <8 \\ \frac{t^2}{10} &; & 8 < t \end{array} \right.$$

SOLUÇÃO: Podemos escrever esta função como $$ f(t) = \left\{ \begin{array}{lll} 3 &; & t <2 \\ 1 &; & 2< t <5 \\ t &; & 5 < t <8 \\ \frac{t^2}{10} &; & 8 < t \end{array} \right. = \left\{ \begin{array}{lll} 3 &; & t <2 \\ 0 &; & t \geq 2 \end{array} \right. + \left\{ \begin{array}{lll}  1 &; & 2< t <5 \\ 0 &; & para\;\;os\;\;demais\;\;valores \end{array} \right. + $$ $$+ \left\{ \begin{array}{lll} t &; & 5 < t <8 \\ 0 &; & para\;\;os\;\;demais\;\;valores \end{array} \right. + \left\{ \begin{array}{lll} 0 &; & t \leq 8 \\ \frac{t^2}{10} &; & 8 < t \end{array} \right. = $$ $$ = 3 \left\{ \begin{array}{lll} 1 &; & t <2 \\ 0 &; & t \geq 2 \end{array} \right. + \left\{ \begin{array}{lll}  1 &; & 2< t <5 \\ 0 &; & para\;\;os\;\;demais\;\;valores \end{array} \right. + $$ $$+ t \left\{ \begin{array}{lll} 1 &; & 5 < t <8 \\ 0 &; & para\;\;os\;\;demais\;\;valores \end{array} \right. + \frac{t^2}{10} \left\{ \begin{array}{lll} 0 &; & t \leq 8 \\ 1 &; & 8 < t \end{array} \right. = $$ $$ =  3 [ 1 -u(t-2) ] + [u(t-2) – u(t-5)] + t [u(t-5) – u(t-8)] + \frac{t^2}{10} u(t-8) = $$ $$ = 3 – 2 u(t-2) + (t-1) u(t-5) + \left( \frac{t^2}{10} -t \right) u(t-8) = $$ $$ =  3 [ 1 -u(t-2) ] + [u(t-2) – u(t-5)] + t [u(t-5) – u(t-8)] + \frac{t^2}{10} u(t-8) = $$ $$ = 3 – 2 u(t-2) + (t-1) u(t-5) + \left( \frac{t^2}{10} -t \right) u(t-8) = $$ $$ = 3 – 2 u(t-2) + (t-1) u(t-5) + \frac{1}{10} \left( t^2 – 10 t \right) u(t-8).$$

Para aplicar a Transformada de Laplace precisamos ajustar algumas destas parcelas para aplicar o teorema da translação observando que $$ (t-1) = (t-5) +4; \qquad ( t^2 – 10 t) = (t-8)^2 + 6(t-8) + 16, $$ podemos reescrever esta função como $$ f(t)= 3 – 2 u(t-2) + [(t-5) +4] u(t-5) + \frac{1}{10} \left( (t-8)^2 + 6(t-8) + 16 \right) u(t-8).$$

Portanto, $$ \mathscr{L}\{f(t) \}  = \mathscr{L}\{ 3 \} – 2 \mathscr{L}\{ u(t-2)\} + \mathscr{L}\{ (t-5)  u(t-5) \} + $$ $$+ 4 \mathscr{L}\{ u(t-5) \} + \frac{1}{10} \mathscr{L}\{ (t-8)^2 u(t-8) \} + $$ $$+ \frac{3}{5} \mathscr{L}\{(t-8) u(t-8)\} + \frac{8}{5} \mathscr{L}\{ u(t-8)  u(t-8) \} = $$ $$ = \frac{3}{s} – \frac{2 e^{-2s}}{s} + e^{-5s} \left( \frac{4}{s} + \frac{1}{s^2} \right) + \frac{e^{-8s}}{5} \left( \frac{1}{s^3} + \frac{3}{ s^2} + \frac{8}{ s} \right)$$

Leia Mais:

• Transformada de Laplace | 1ª Lista de Exercícios Resolvidos
• Transformada de Laplace | Das Definições Básicas à Função Delta
• Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos
• Solução da Prova Sobre Transformada de Laplace 2020/2

Video-Aulas Sobre Transformada de Laplace: