Circuitos em Série | Aplicações da Transformada de Laplace

Em um circuito em série, a segunda lei de Kirchhoff diz que a soma da queda de tensão em um indutor, resistor e capacitor é igual à voltagem expressa E(t) . Os circuitos elétricos muitas vezes são governados por equações diferenciais, desde as mais simples até os modelos matemáticos não-lineares mais complexos e, por consequência, equações integro-diferenciais. Neste artigo queremos explorar os circuitos em série neste último contexto.

Sabemos que a queda de tensão através do indutor \left( L \dfrac{di}{dt} \right) , através do resistor \left(R i(t) \right) , e do capacitor \left( \dfrac{1}{C} \int\limits_{0}^{t}{i( \tau ) d \tau} \right) ,, em que i(t) é a corrente e L, R \text{ e } C são constantes. Segue que a corrente em um circuito como o da figura abaixo satisfaz a equação integro-diferencial $$ L \frac{di}{dt} + R i + \frac{1}{C} \int\limits_{0}^{t}{i( \tau ) d \tau} = E(t)$$

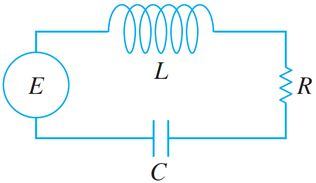
É importante lembrar que as equações diferenciais que descrevem vibrações mecânicas e circuitos em série RLC são basicamente a as mesmas. E, de fato, existe uma identificação natural dos parâmetros m, b, \text{ e } k para o sistema mass-mola com os parâmetros L, R \text{ e } C , que descrevem circuitos.

Transformada de Laplace Aplicada aos Circuitos em Série – Exercícios Resolvidos

1) Determine a corrente i(t) em um circuito em série L-R-C quando L = 0,1 henry, R = 20 ohms, C = 10^{-3} farad, i(0) = 0 e a voltagem impressa E(T) é como dada na figura abaixo:

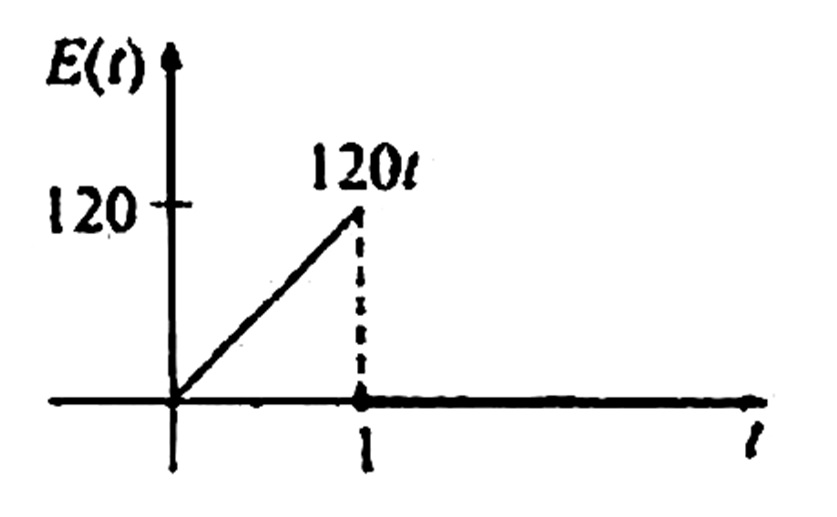
SOLUÇÃO: Como a voltagem está desligada para t \geq 1 , podemos escrever $$E(t) = 120 t – 120 u(t-1) . $$ Mas, para usarmos o teorema da Translação, devemos reescrever este termo como $$E(t) = 120 t – 120(t-1)u(t-1)-120 u(t-1)$$. A equação integro-diferencial que modela este problema será dada, então, por $$ 0,1 \frac{d i}{dt} + 20 i +10^3 \int\limits_{0}^{t}{i(\tau ) d \tau } = 120 t – 120(t-1)u(t-1)-120 u(t-1)$$ Agora, segue da Transformada da integral que $$ \mathscr{L} \left\{ \int\limits_{0}^{t}{i(\tau ) d \tau } \right\} = \frac{I(s)}{s}, $$ onde \mathscr{L} \left\{ i(t) \right\} = I(s) . Logo a Transformada da equação integro-diferencial que modela o problema será dada por $$ 0,1 I(s) + 20 I(s) +10^3 \frac{I(s)}{s} = 120 \left[ \frac{1}{s^2} – \frac{1}{s^2} e^{-s} – \frac{1}{s} e^{-s} \right], $$ ou, após multiplicar por 10 s , $$(s+100)^2 I(s) = 1200 \left[ \frac{1}{s} – \frac{1}{s} e^{-s} – e^{-s} \right]$$ $$I(s) = 1200 \left[ \frac{1}{s(s+100)^2} – \frac{1}{s (s+100)^2} e^{-s} – \frac{1}{(s+100)^2} e^{-s} \right].$$ Usando Frações Parciais, podemos escrever $$ I(s) = 1200 \left[ \frac{1}{10 000s} – \frac{1}{10000 (s+100)}  – \frac{1}{100(s+100)^2} – \frac{1}{10 000 s} e^{-s} + \\ + \frac{1}{10000 (s+100)} e^{-s} + \frac{1}{100(s+100)^2} e^{-s} – \frac{1}{(s+100)^2} e^{-s} \right]$$

Empregando a forma inversa do segundo teorema de translação, obtemos $$ i(t) = \frac{3}{25} \left[ 1 – u(t-1) \right] – \frac{3}{25} \left[ e^{-100 t} – e^{-100 (t-1)}u(t-1) \right] – \\ -12 t e^{-100 t} – 1188(t-1) e^{-100 (t-1)}u(t-1) .$$

2) A equação diferencial para a corrente i(t) em um circuito em série L-R é $$L \frac{d i}{dt} + R i = E(t).$$ Determine a corrente i(t) quando i(0) = 0 e E(t) é a função representada pela onda retangular:

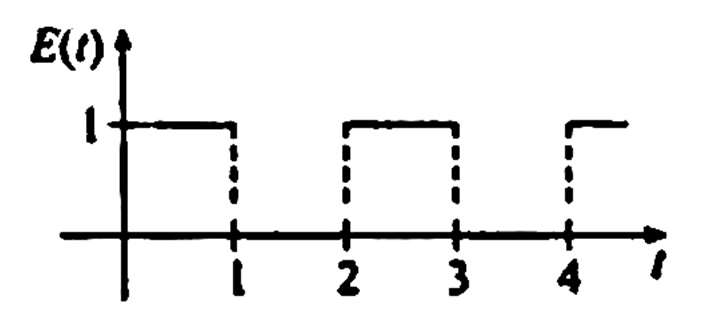
SOLUÇÃO: A transformada de Laplace da equação é $$ Ls I(s) + R I(s) = \mathscr{L} \left\{ E(t) \right\} .$$ Como E(t) é periódica com período T = 2 . Assim, usando a fórmula da transformada de Laplace de uma função periódica \begin{eqnarray} \mathscr{L} \left\{ E(t) \right\} & = & \frac{1}{1 – e^{-2s}}\int\limits_{0}^{2}{e^{-st} f(t) dt}\\ & = & \frac{1}{1 – e^{-2s}}\int\limits_{0}^{1}{1 \times e^{-st} dt}\\ & = & \frac{1}{1 – e^{-2s}} \frac{1 – e^{-s}}{s}\\ & = & \frac{1}{s \left( 1 – e^{-s} \right)} \end{eqnarray}

Agora, aplicando a transformada de Laplace na equação diferencial e isolando I(s) obtemos $$ I(s) = \frac{1/L}{s(s+R/L) \left(1 + e^{-s} \right)} .$$ Para encontrar a transformada de Laplace inversa desta função, usamos primeiramente uma série geométrica. Lembre -se que , para | x| < 1 , $$ \frac{1}{1+x} = 1 – x +x^2 – x^3 + …. $$ e substituindo x por e^{-s}, s>0 , temos, $$ \frac{1}{1+e^{-s}} = 1 – e^{-s} +e^{-2s} – e^{-3s} + …. .$$ Usando este fato e escrevendo $$ \frac{1}{s(s+R/L)} = \frac{L/R}{s} – \frac{L/R}{s + R/L}$$ obtemos $$ I(s) = \frac{1}{R} \left( \frac{1}{s} – \frac{1}{s+R/L} \right) 1 – e^{-s} +e^{-2s} – e^{-3s} + …. = \\ = \frac{1}{R} \left( \frac{1}{s} – \frac{e^{-s}}{s} + \frac{e^{-2s}}{s} – \frac{e^{-3s}}{s} + ….\right) – \\ – \frac{1}{R} \left( \frac{1}{s+R/L} – \frac{e^{-s}}{s+R/L} + \frac{e^{-2s}}{s+R/L} – \frac{e^{-3s}}{s+R/L} + ….\right).$$

Empregando a forma inversa do segundo teorema de translação em cada termo de ambas as séries, obtemos $$i(t) = \frac{1}{R} \left[ 1 – u(t-1) + u(t-2) – u(t-3) +…. \right]- \\ – \frac{1}{R} \left[ e^{-Rt/L} – u(t-1) e^{-R(t-1)/L}+ u(t-2) e^{-R(t-2)/L} – u(t-3) e^{-R(t-3)/L} +…. \right] = \\ = \frac{1}{R} \left[ 1 – e^{-Rt/L} \right] + \frac{1}{R} \sum\limits_{n = 1}^{\infty}{(-1)^n \left[ 1 – e^{-R(t-n)/L} u(t-n) \right]}.$$

REDES ELÉTRICAS – Sistema de Equações Diferenciais de 1ª Ordem

Uma rede elétrica com mais de uma malha também dá origem a equações diferenciais simultâneas. Conforme vemos na ilustração abaixo, a corrente i_1 (t) se bifurca nas direções indicadas no ponto B_1 , chamado ponto de ramificação da rede. 

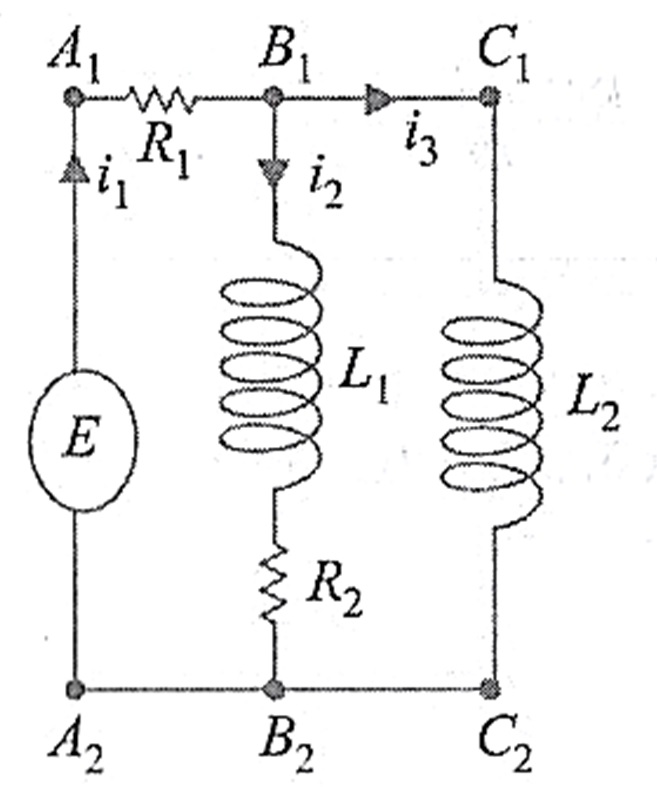
Pela primeira lei de Kirchhoff, podemos escrever $$ i_1 (t) = i_2 (t) + i_3 (t). \tag{1}$$ Além disso, podemo também aplicar a segunda lei de Kirchhoff a cada malha. Para a malha A_1 B_1 B_2 A_2 A_1 , somando as quedas de voltagem através de cada parte da malha, obtemos $$E(t) = i_1 R_1 + L_1 \frac{d i_2 }{dt}+ i_2 R_2.$$ Analogamente, para a malha A_1 B_1 C_1 C_2 A_2 A_1 , temos $$ E(t) = i_1 R_1 + L_2 \frac{d i_3 }{dt}.$$ Utilizando (1) para eliminar i_1 nas duas equações diferenciais, obtemos um sistema de equações diferenciais de primeira ordem para as correntes i_2 (t) e i_3 (t) \begin{eqnarray} L_1 \frac{d i_2 }{dt} + (r_1 + R_2) i_2 + R_1 i_3 & = & E(t) \\ L_2 \frac{d i_3 }{dt} + R_1  i_2 + R_1 i_3 & = & E(t) \end{eqnarray}, onde dadas as condições iniciais adequadas podemos usar a Transformada de Laplace para solucionar.

Usando um raciocínio análogo, podemos mostrar que o sistema de equações diferenciais que descrevem as correntes i_1 (t) e i_2 (t) na rede que contém um resistor, um indutor e um capacitor conforme a figura abaixo,

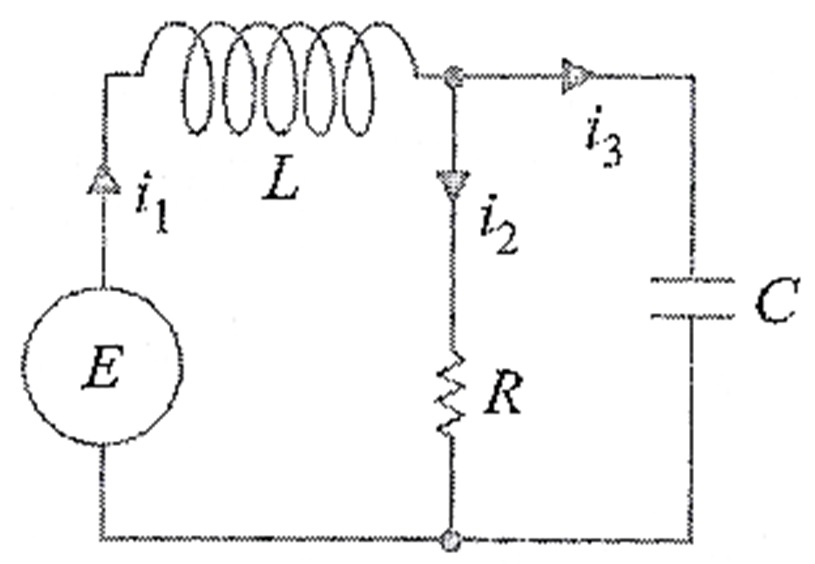
é \begin{eqnarray} L \frac{d i_1 }{dt} + R i_2 + R_1 i_3 & = & E(t) \\ RC \frac{d i_2 }{dt} +  i_2 – i_1 & = & 0 \end{eqnarray}.

BIBLIOGRAFIA:

1. Nagle, Kent R. e Saff, Edward B.. “Equações Diferenciais” (Link para comprar o livro)
2. Zill,, Dennis. “Equações diferenciais: Com aplicações em modelagem”. (Link para comprar o livro)

Leia Mais:

• Transformada de Laplace Inversa | Lista de Exercícios Resolvidos
• Equação Integral de Volterra | Convolução e Transformada de Laplace
• Solucionando Eq. Diferenciais Ordinárias Via Transformada de Laplace
• Função de Heaviside ou Degrau Unitário | Transformada de Laplace e o Teorema da Translação

Listas de Exercícios sobre Transformada de Laplace:

• Transformada de Laplace | 1ª Lista de Exercícios Resolvidos
• Transformada de Laplace | 2ª Lista de Exercícios Resolvidos
• Transformada de Laplace | 3ª Lista de Exercícios Resolvidos
• Transformada de Laplace | 4ª Lista de Exercícios Resolvidos