Compreendendo as Seções Cônicas: Um Guia Introdutório

As cônicas, ou seções cônicas, são um tema importante no estudo da matemática. Este guia para iniciantes o ajudará a entender os fundamentos dessas curvas (parábola, hipérbole e elipse) e suas aplicações.

As cônicas, também conhecidas como seções cônicas, são um grupo de curvas estudadas na matemática há séculos. Essas curvas são formadas pela interseção de um plano e um cone e têm uma ampla gama de aplicações em áreas como engenharia, física e astronomia. Neste guia para iniciantes, exploraremos os fundamentos das cônicas e suas propriedades.

A apresentação matemática das cônicas é principalmente no estilo da geometria analítica cujas origens são dadas a Descartes. Porém, as definições das seções cônicas apresentadas abaixo eram aparentemente conhecidos por matemáticos do leste Mediterrâneo na Antiguidade. As seções cônicas são dignas
de estudo, independentemente de qualquer abordagem. No entanto, Isaac Newton (1643–1727), por exemplo, não poderia ter desenvolvido sua teoria da
gravitação sem saber o que os antigos sabiam sobre seções cônicas.

Conhecendo o Cone

Um cone e sua superfície cônica associada são determinada pelos seguintes dados:

1. um círculo, chamado de base do cone;
2. um ponto, denominado vértice do cone e da superfície cônica; o vértice não deve estar no plano da base.

A superfície cônica consiste nos pontos das linhas que passam pelo vértice e a circunferência da base. O cone em si é o sólido figura delimitada pela superfície e pela base.

As definições de cone e superfície cônica podem ser encontradas no início do tratado “Sobre as seções Cônicas”, de Apolônio de Perga. O eixo do cone é a linha que une o vértice ao centro da base. Não há nenhuma suposição de que o eixo é perpendicular à base; se for, então o cone é reto caso contrário, o cone é oblíquo.

O que é uma Seção Cônica?

Uma seção cônica é a interseção de um plano com uma cônica superfície. A descoberta de seções cônicas (como objetos dignos de estudo) é geralmente atribuído ao predecessor de Apolônio, Menaechmus. No entanto, existem três tipos de seções cônicas: a elipse, a parábola e a hipérbole. De acordo com Eutócio, Apolônio foi o primeiro matemático para mostrar que cada tipo de seção cônica pode ser obtido de toda superfície cônica. De fato, os nomes dos três tipos de seções cônicas parecem ser devido a Apolônio também. Os nomes são significativos em grego e refletem as diferentes propriedades geométricas das
seções cônicas.

As Seções Cônicas

Uma seção cônica \zeta é determinada pelos seguintes dados:

1. uma linha d , chamada de diretriz de \zeta;
2. um ponto F (não em d ), chamado de foco de \zeta ;
3. um número real positivo (ou distância) e , chamado de excentricidade de \zeta .

Então \zeta compreende os pontos P (no plano de d e F ) de tal modo que $$ d(P,F)=e\times d(P,d). $$

As Seções Cônicas em Coordenadas No Plano

Suponha que atribuímos um sistema de coordenadas retangulares ao plano de \zeta em que F tem as coordenadas (h,k), e d é definido por \begin{equation} Ax+By+C=0 \end{equation} (onde A\neq 0 ou B\neq 0). Então \zeta é definido por \begin{equation} \sqrt{(x-h)^2+(y-k)^2}=e\cdot\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}, \end{equation}
daí também por \begin{equation} (x-h)^2+(y-k)^2=e^2\cdot\frac{(Ax+By+C)^2}{A^2+B^2} \qquad (1) \end{equation}

Esta equação não é muito útil para mostrar a forma de \zeta . Ao escolher o sistema de coordenadas retangulares apropriadamente, podemos, sem perda de generalidade, atribuir \begin{equation} (h,k)=(0,0), \quad B=0, \quad A=1,\quad C>0. \end{equation} Então C é a distância entre o foco e a diretriz, e  torna-se \begin{equation}  x^2+y^2=e^2(x+C)^2 \qquad (2) \end{equation}

Uma ideia central da Geometria analítica é a de associar a cada uma das curvas geradas pelas seções cônicas uma equação que relaciona a abicissa com a ordenada de cada ponto desta curva. Uma vez obitida esta equação, as propriedades geometricas da curva podem ser deduzidas por métodos algébricos. Abaixo iremos deduzir as equações principais destas cônicas partindo de suas definições geométricas, mas registramos que temos artigos específicos para cada uma delas com todos os detalhes técnicos.

A Equação da Circunferência

Dados os pontos A (a,b) e o número real r>0 , a circunferência C de centro A e raio r é, como se sabe, o conjunto dos pontos do plano situados à distância r do ponto A . Assim, o ponto P(x,y) pertence a C se, e somente se, $$d(A,P) = r.$$ Levando em conta a fórmula da distância entre dois pontos no plano podemos escrever $$C = \left\{ (x,y)\in \mathbb{R}^2 ; \sqrt{(x-a)^2 + (y-b)^2} = r  \right\} .$$

Equivalentemente, podemos dizer que o ponto P(x,y) pertence à circunferência C se, e somente se, $$(x-a)^2 + (y-b)^2 = r^2$$ e esta é a equação da circunferência de centro (a,b) e raio r no plano cartesiano.

A Equação da Elipse

Um elipse com focos F e F' é o conjunto dos pontos P do plano cuja somas das distâncias a F e F' é igual uma constante denotada por 2a . É conveniente escolher um sistema de eixos tal que os os focos tenham coordenadas F(c,0) e F' (-c,0) . A distância 2c   entre os focos é chamada de distância focalda eleipse.

Um ponto P(x,y) pertence à elipse quando $$ d(P,F)+d(P,F’) = 2a $$ isto é $$\sqrt{(x-c)^2 +(y-0)^2} + \sqrt{(x+c)^2 +(y-0)^2} = 2a $$ $$\sqrt{(x-c)^2 +y^2}  = 2a – \sqrt{(x+c)^2 +y^2}$$ Elevando ambos os membros ao quadrado, obtemos $$ (x-c)^2 +y^2 = 4a^2 – 4a\sqrt{(x+c)^2 +y^2}+ (x+c)^2 +y^2$$ que, após simplificações, resulta $$ a \sqrt{(x+c)^2 +y^2} = a^2 +cx.$$ Elevando novamente ao quadrado: $$ a^2 (x^2+2cx+c^2 +y^2) = a^4 +2a^2cx+c^2 x^2,$$ e daí, $$(a^2-c^2)x^2+a^2y^2 = a^2 (a^2 – c^2).$$ É usual representar a diferença a^2 - c^2 por b^2 . A equação pode então ser escrita na forma $$b^2x^2 +a^2 y^2 = a^2 b^2.$$ Dividindo ambos os membros por a^2 b^2 obtemos finalmente $$ \frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1,$$ que é a forma mais usual de escrever a equação da elipse.

É fácil verificar que os pontos A(a,0) , A'(-a,0) , B(0,b) e B'(0,-b) (chamados de vértices) pertencem à elipse. Os segmentos AA' e BB' são eixos de simetria da elipse e são chamados de eixo maior (ou focal) e eixo menor (ou transverso).

A Equação da Hipérbole

Analogamente ao processo que usamos para a elipse, podemos obter a equação da hipérbole, que é definida como o conjunto dos pontos cuja diferença (em valor absoluto) das distâncias aos focos F e F' é uma constante denotada por 2a . Se tomarmos os eixos de forma que os focos sejam novamente F(c,0) e F' (-c,0) a equação obtida é $$ \frac{x^2}{a^2} – \frac{y^2}{b^2} = 1 ,$$ onde b^2 satisfaz a^2 + b^2 = c^2 .

Os pontos A(a,0) , A'(-a,0) (chamados de vértices) pertencem à hipérbole e determinam um de seus eixos de simetria (o eixo focal ou real). Os pontos B(0,b) e B'(0,-b) são denominados vértices imaginários e determinan o eixo transverso, ou imaginário, da hipérbole. O retângulo cujos eixos de simetria são AA' e BB' está estreitamente relacionado com a geometria da hipérbole: sua diagonais são assíntotas da hipérbole.

A Equação da Parábola

Finalmente, consideramos a parábola de foco F e diretriz d , que é o conjunto dos pontos P que são equidistantes do ponto F e a reta d . É usual escolher um sistema de eixos coordenados no qual F\left( 0 , \dfrac{p}{2}\right) e d como a reta horizontal de equação y = - \dfrac{p}{2} (a distância p entre  F e a reta d é chamada de parâmetro da parábola). Neste sistema, a parábola contém a origem e é simétrica em relação ao eixo vertical Oy.

A distância de P à d é dada por \left| y + \dfrac{p}{2} \right| , enquanto a distância de P a F é \sqrt{(x-0)^2 + \left( y - \dfrac{p}{2}\right)^2} . Logo, a equação da parábola é $$ \sqrt{x^2 + \left( y – \frac{p}{2}\right)^2} = \left| y + \frac{p}{2} \right|.$$ Elevando ao quadrado, obtemos $$ x^2 + y^2 – py + \frac{p^2}{4} = y^2 +py + \frac{p^2}{4} $$ e finalmente $$ y = \frac{1}{2p} x^2.$$

Seções Cônicas: O Caso Geral

A equação geral do 2º grau a duas variáveis $$ax^2 + by^2 + 2cxy + dx +ey + f = 0,$$ onde pelo menos uma dos coeficientes a, b, c é diferente de zero, representa uma parábola, uma elipse ou uma hipérbole.

Sejam duas retas e e r concorrentes em O e não perpendiculares. Conservemos fixa a reta e e façamos girar 360º em torno de e mantendo constante o ângulo entre estas retas. Nestas condições, a reta r gera uma superfície cônica circular infinita formada por duas folhas separadas pelo vértice O , conforme a figura abaixo:

A reta r é chamada geratriz da superfície cônica e a reta e , eixo da superfície.

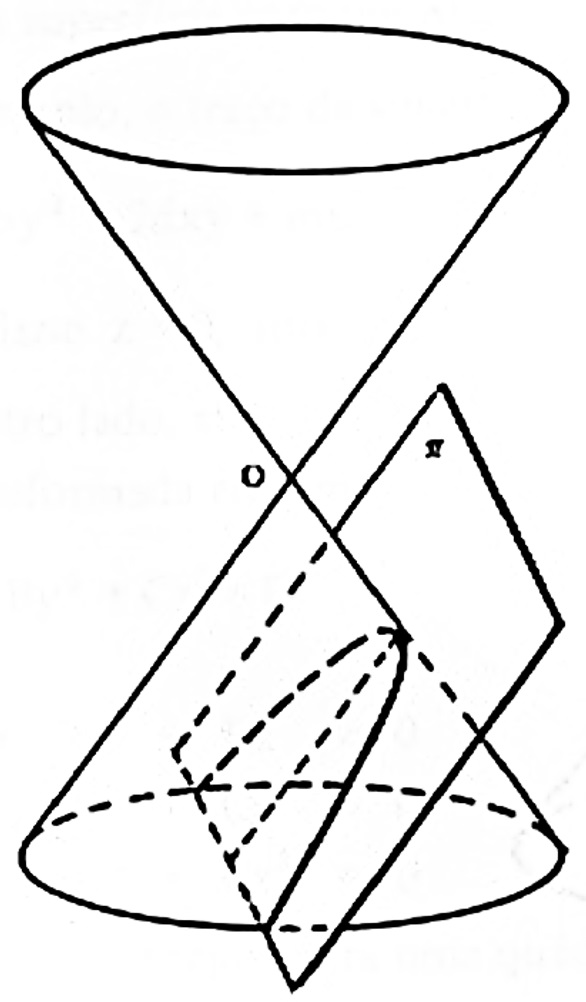
Chama-se seção cônica ao conjunto de pontos que formam a interseção de uma plano com a superfície cônica. Quando uma superfície cônica é seccionada por plano \pi qualquer que não passa pelo vértice O , a seção cônica será:

1. Uma circunferência  se \pi for perpendicular ao eixo e da superfície;
2. uma elipse se \pi for oblíquo ao eixo e , cortando apenas uma das folhas da superfície;
3. uma parábola se \pi for paralelo à geratriz r ;
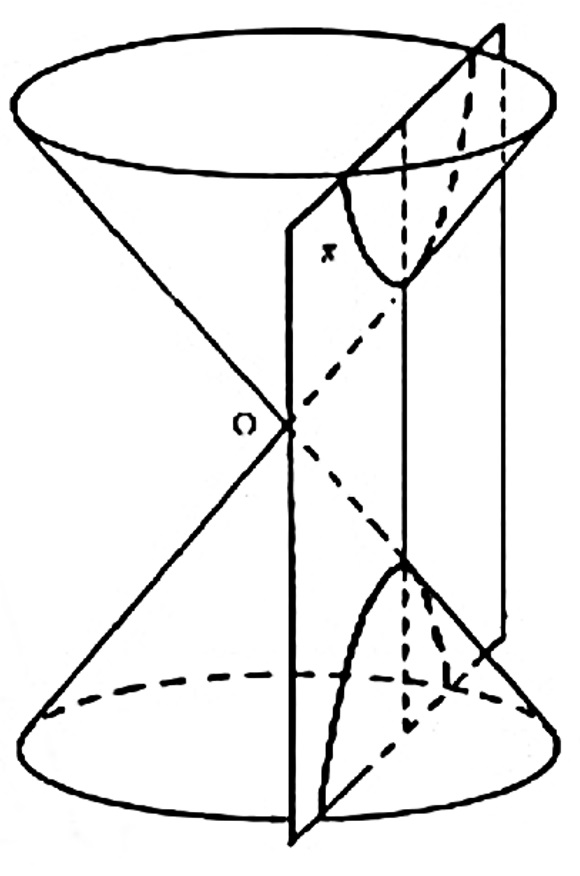
4. uma hipérbole se \pi for paralelo ao eixo e ;
5. um ponto se o plano \pi só tem o ponto O em comum coma superfície;
6. uma reta se \pi tangencia a superfície cônica;
7. duas retas se \pi forma com o eixo um ângulo menor do que este faz com a geratriz.

Leia Mais:

• Retas No Plano Cartesiano: Posições Relativas Entre Retas
• Retas no Plano Cartesiano: Equações Reduzida, Geral, Vetorial e Paramétrica
• Vetores no Plano R²: Norma e Produto Escalar
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• O Espaço R²: Coordenadas no Plano Cartesiano
• Curvas no Espaço | Parametrização de Curvas Clássicas