Vetores no Plano R²: Norma e Produto Escalar

Em matemática e física, normas e produtos escalares são conceitos fundamentais que nos ajudam a entender o comportamento dos vetores no espaço. Neste guia, forneceremos uma abordagem passo a passo para calcular normas vetoriais e produtos escalares.

Um sistema de eixos ortogonais num plano \pi é um par de eixos Ox e Oy , tomados em \pi , que são perpendiculares e têm a mesma origem O . Diz-se que o eixo Ox é horizontal e o eixo Oy é vertical. Um plano \pi munido de um sistema de eixos ortogonais põe-se, de modo natural, em correspondência biunívoca com o conjunto \mathbb{R} ^2 . Dado o ponto P do plano, baixamos por ele paralelas aos eixos Ox e Oy . Estas retas paralelas cortam os eixos em pontos cijas coordenadas são x e y respectivamente.

Ao ponto P do plano \pi faz-se corresponder o par ordenado (x,y) \in \mathbb{R} ^2. Reciprocamente, a cada par ordenado (x,y) \in \mathbb{R} ^2 corresponde a um ponto P \in \pi . Os números x e y chama-se coordenadas cartesianas do ponto P relativamente ao sistema de eixos ortogonais fixado: x é a abcissa e y a ordenada de P .

Em todo o nosso estudo sobre geometria analítica, a menos que seja feita explicitamente uma menção em contrário, admitiremos que foi fixado um sistema de eixos ortogonais no plano, que assim se identifica a \mathbb{R} ^2. Cada ponto P(x,y) do plano passa a ser a mesma coisa que um par ordenado de números reais.

Os eixos ortogonais decompões o plano em quatro regiões, chamados quadrantes. Tem-se o primeiro quadrante, formado pelos pontos que têm ambas coordenadas positivas. No segundo quadrante, a abcissa é negatica e a ordenada é positiva. No terceiro quadrante, abcissa e ordenada são ambas negativas. No quarto quadrante, os pontos têm abcissa positiva e ordenada negativa.

Expressão Analítica de um Vetor no Plano

Fixada a base canônica \left\{ \vec{i} , \vec{j} \right\}, fica estabelecida uma correspondência biunívoca entre os vetores do plano e os pares ordenados (x,y) de números reais. Nestas condições definimos um vetor no plano como um par ordenado (x,y) de números reais representado por \vec{v} = (x,y) que é a expressão analítica de \vec{v} . A primeira componente x é chmada abscissa e a segunda, ordenada.

OBSERVAÇÃO: Deve ter ficado claro que a escolha proposital da base \left\{ \vec{i} , \vec{j} \right\} deve-se à simplificação. Assim, para exemplificar, quando nos referimos a uma ponto P(x,y) , ele pode ser identificado com o vetor \vec{v} = \vec{OP} = x \vec{i} + y \vec{j} , sendo ) a origem do sistema como na figura abaixo:

Desta forma, o plano cartesiano pode ser encarado como um conjunto de pontos ou um conjunto de vetores.

Inúmeras vezes um vetor é representado por um segmento orientado que não parte que não parte da origem do sistema. Considerando o vetor \vec{AB} de orgiem no ponto A(x_1, y_1) e extremidade em B(x_2,y_2) , as componentes de  \vec{AB} podem ser encontradas da seguinte maneira $$ \vec{AB}  = \left( x_2 – x_1 , y_2 – y_1 \right)$$ a razão pela qual também se escreve que $$ \vec{AB} = B – A .$$ Esta última é chamada de notação de Grassmann e não se trata à rigor de subtrair pontos, mas sim de uma notação sugestiva, já que o ponto B é a soma do ponto A com o vetor \vec{AB} .

È melhor pensar que ela seria uma simplificação da notação $$ \vec{AB} = \vec{OB} – \vec{OA}$$ como nos infere a imagem abaixo:

A Norma de um Vetor no Plano

Dado um ponto P( x, y) , o comprimento do segmento de reta \overline{OP} é, como sabemos (por este artigo), igual a $$ \sqrt{x^2 + y^2} .$$ Diremos também que este é o comprimento do vetor \vec{OP} e escrevemos $$ | \vec{v} | = | \vec{OP} | = | (x,y)| = \sqrt{x^2 + y^2} .$$ Se | \vec{v} | = 1 então diremos que \vec{v} é um vetor unitário.

EXEMPLO: Se \vec{v} = (2,1) então $$ | \vec{v} |= \sqrt{2^2 + 2^2} = \sqrt{5} $$.

EXEMPLO (versor de um vetor \vec{u} ): O versor do vetor \vec{u} = (a,b) é o vetor \vec{v} , dado por $$ \vec{v} = \frac{1}{| \vec{u} |} \vec{u} = \frac{1}{\sqrt{a^2 +b^2}} (a,b) = \left( \frac{a}{\sqrt{a^2 +b^2}} , \frac{b}{\sqrt{a^2 +b^2}} \right).$$ O versor do vetor \vec{u} é um vetor unitário, com mesma direção e sentido de \vec{u} . De fato, podemos mostrar facilmente que o versor de \vec{u} é unitário: $$ |  \vec{v} | = \left| \left( \frac{a}{\sqrt{a^2 +b^2}} , \frac{b}{\sqrt{a^2 +b^2}} \right) \right| = \sqrt{ \left( \frac{a}{\sqrt{a^2 +b^2}} \right)^2 + \left( \frac{b}{\sqrt{a^2 +b^2}} \right)^2 } = \sqrt{\frac{a^2}{a^2 +b^2} + \frac{b^2}{a^2 +b^2} } = \sqrt{\frac{a^2 + b^2}{a^2 +b^2}} = \sqrt{1} = 1.$$

OBSERVAÇÕES:

1. O Versor de um vetor: O versos de um vetor \vec{v} é um vetor \vec{u} , unitário, com a mesma direção e o mesmo sentido de \vec{v} . Portanto o versor de um vetor \vec{v} é dado pela fórmula $$ \vec{u} = \frac{1}{| \vec{v} |} \vec{v}.$$
2. A Distância entre dois pontos: a distância d entre dois pontos A \left( x_1 , y_1 \right) e B \left( x_2 , y_2 \right)   é definida como a norma, ou o módulo, do vetor \vec{AB} , ou seja $$ d(A,B) = | \vec{AB}| = |B-A| = \sqrt{ \left( x_2 – x_1 \right)^2+ \left( y_2 – y_1 \right)^2}.$$

O Produto Escalar (ou Produto Interno Usual) no Plano

Chama-se produto escalar (ou produto interno usual) de dois vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} \qquad \text{e} \qquad \vec{v} = x_2 \vec{i} + y_2 \vec{j} $$ e se representa por \vec{u} \cdot \vec{v} , ao número real $$  \vec{u} \cdot \vec{v} = x_1 x_2 + y_1 y_2 .$$ O produto escalar de \vec{u} por \vec{v} também é indicado por \langle \vec{u} , \vec{v} \rangle e se lê ” \vec{u} escalar \vec{v} “. Observando que $$ \vec{v} \cdot \vec{v} = x^2 + y^2 $$ então podemos escrever que $$ | \vec{v} |= \sqrt{ \vec{v} \cdot \vec{v} }.$$

EXEMPLO: Se \vec{u} = (3,-5) e \vec{v} =(4,-2) tem-se \vec{u} \cdot \vec{v} = 3 \times 4 + -5 \times (-2) = 12 + 10 = 22 .

Propriedades do Produto Escalar

Para quaisquer que sejam os vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} \qquad  \vec{v} = x_2 \vec{i} + y_2 \vec{j} \qquad \text{e} \qquad \vec{w} = x_3 \vec{i} + y_3 \vec{j}, \qquad \alpha \in \mathbb{R} $$ temos que:

1. \vec{u} \cdot \vec{u} \geq 0 e \vec{u} \cdot \vec{u} = 0 se, e somente se, \vec{u} = \vec{0} ;
2. \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u} ;
3. \vec{u} \cdot \left( \vec{v} + \vec{w} \right)= \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w};
4. \left( \alpha \vec{u} \right) \cdot \vec{v} = \alpha \left( \vec{u} \cdot \vec{v}  \right) = \vec{u} \cdot \left( \alpha \vec{v} \right) ;
5. \vec{u} \cdot \vec{u} = | \vec{u} | ^2 .

OBSERVAÇÃO: Ao definirmos o produto escalar de dois vetores por meio de suas coordenadas, devemos nos perguntar se o produto escalar se alteraria caso tomássemos outra base ortonormal para o espaço euclidiano \mathbb{R} ^2 . O teorema que enunciaremos abaixo, que nos dá a fórmula para calcular o ângulo entre dois vetores no plano nos autoriza a dizer que o produto interno se mantem inalterado por ser o produto dos tamanhos dos vetores com o cosseno do ângulo entre os dois vetores. Um exemplo interessante deste fato se encontra no livro “Coordenadas no Plano”, de Elon Lages Lima (confira o livro neste link).

A Interpretação Geométrica do Produto Escalar de Dois Vetores

Vamos dar o significado geométrico do produto escalar entre dois vetores.

1) FÓRMULA PARA O ÂNGULO ENTRE DOIS VETORES:

Teorema: Se \theta é o ângulo entre os vetores \vec{u} e \vec{v} , então \vec{u} \cdot \vec{v} =| \vec{u} | | \vec{v} | \text{cos} ( \theta ) .

Portanto, por este Teorema podemos concluir que o ângulo entre os vetores \vec{u} e \vec{v} é dado por $$ \theta = \text{arc cos}\left( \frac{\vec{u} \cdot \vec{v}}{| \vec{u} | | \vec{v} |} \right).$$

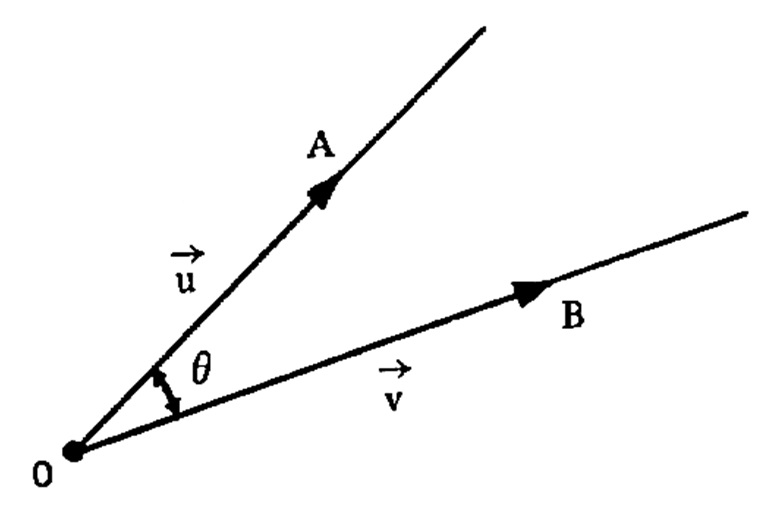
O ângulo de dois vetores   \vec{u} e   \vec{v} não nulos é o ângulo \theta formado pelas semi-retas OA e OB , tal que 0 \leq \theta \leq \pi , como na figura abaixo:

OBSERVAÇÕES:

1. Se \theta = \pi , então   \vec{u} e   \vec{v} têm a mesma direção e sentidos opostos;
2. Se \theta = 0 , então   \vec{u} e   \vec{v} têm a mesma direção e o mesmo sentido;
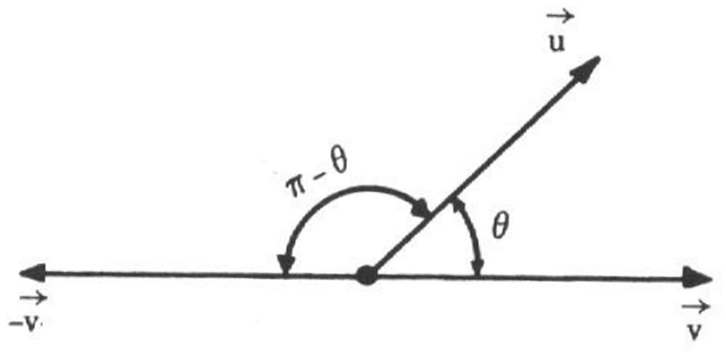
3. O ângulo formado pelos vetores   \vec{u} e - \vec{v} é o suplemento do ângulo de   \vec{u} e   \vec{v} , como na figura abaixo:
   

   

4. Se \theta = \dfrac{\pi}{2} , então   \vec{u} e   \vec{v} são ortogonais e indica-se \vec{u} \bot \vec{v} ; Neste caso, o triângulo retângulo OBC permite escrever $$ | \vec{u} + \vec{v} | ^2 = | \vec{u} | ^2 + | \vec{v} |^2 .$$
5. O vetor nulo é ortogonal a qualquer vetor;
6. Se   \vec{u} é ortogonal a   \vec{v} e m é um número real qualquer,   \vec{u} é ortogonal a   m \vec{v} .

2) CONDIÇÃO DE PERPENDICULARISMO ENTRE DOIS VETORES:

Teorema: Os vetores \vec{u} e \vec{v} são perpendiculares se, e somente se, \vec{u} \cdot \vec{v} = 0 .

Uma demonstração deste teorema pode ser feita rapidamente da seguinte maneira:

( \Rightarrow ) Como \vec{u} e \vec{v} são perpendiculares, então, pelo Teorema de Pitágoras nos dá $$ | \vec{u} + \vec{v} |^2 = | \vec{u} |^2 + | \vec{v} |^2.$$ Mas, $$ | \vec{u} + \vec{v} |^2 = \left( \vec{u} + \vec{v} \right) \cdot \left( \vec{u} + \vec{v} \right) = | \vec{u} |^2 + |\vec{v}|^2 + 2 \vec{u} \cdot \vec{v}.$$ Desta forma, $$  | \vec{u} |^2 + | \vec{v} |^2 = | \vec{u} |^2 + |\vec{v}|^2 + 2 \vec{u} \cdot \vec{v}.$$ Logo, $$ 2 \vec{u} \cdot \vec{v} = 0 \Rightarrow  \vec{u} \cdot \vec{v} = 0.$$ Portanto, se  \vec{u} e \vec{v} são perpendiculares então \vec{u} \cdot \vec{v} = 0 .

( \Leftarrow ) Por outro lado, se \vec{u} \cdot \vec{v} = 0 . então o ângulo entre estes dois vetores satifaz a condição $$ \vec{u} \cdot \vec{v} =| \vec{u} | | \vec{v} | \text{cos} ( \theta ) \Rightarrow 0 = | \vec{u} | | \vec{v} | \text{cos} ( \theta ).$$ Se | \vec{u} | = 0 ou  | \vec{v} | = 0 então um deles, ou ambos, é o vetor nulo, portanto são perpendiculares. Supondo agora que | \vec{u} | \neq 0 ou  | \vec{v} | \neq 0 , então nenhum deles pode ser o vetor nulo e ainda teremos que $$ \text{cos} ( \theta ) = 0 \Rightarrow \theta = \frac{ \pi }{2} .$$ Portanto, o ângulo entre os vetores é reto, garantindo a perpendicularidade entre \vec{u} e \vec{v} .

3) PROJEÇÃO ORTOGONAL DE VETORES NO PLANO:

Sejam \vec{u} e \vec{v} , ambos vetores não-nulos, e \theta o ângulo formado entre eles. Então o vetor $$ \vec{w} = \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} $$ é a projeção de \vec{u} sobre \vec{v} .

A notação usual da a projeção de \vec{u} sobre \vec{v} é dada por $$ \text{proj}_{\vec{v}} \vec{u} =  \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} = \left( \frac{\vec{u} \cdot \vec{v}}{\vec{v} \cdot \vec{v}} \right) \vec{v}$$  e esta projeção de vetores é representada nas figuras abaixo.

4) ÁREAS DO PARALELOGRAMO E DO TRIÂNGULO:

Considerando o paralelogramo ABCD no plano. Colocando \vec{AB} = \vec{v} = (\alpha , \beta ) e \vec{AC} = \vec{v} = ( \gamma , \delta ). A área do paralelogramo é dada pelo módulo do determinante $$ \left|\begin{array}{cc} \alpha & \gamma \\ \beta & \delta \\ \end{array} \right| = \alpha \delta – \beta \gamma$$ ou seja, $$ \text{área de ABCD} =  | \alpha \delta – \beta \gamma | .$$

Considerando, agora, o triângulo com vértices A\left( x_1 , y_1\right) , B\left( x_2 , y_2\right) e C\left( x_3 , y_3\right) . A área do triângulo ABC é a metade da área do paralelogramo ABCD . Portanto, lembrando que \vec{AB} = \vec{v} = (\alpha , \beta ) = \left(x_2 - x_1 , y_2 - y_1\right) e \vec{AC} = \vec{v} = ( \gamma , \delta ) = \left( x_3 - x_1 , y_3 - y_1\right) , então a área do triângulo ABC é dada pelo módulo do determinante $$ \left|\begin{array}{cc} x_2 – x_1 & y_2 – y_1 \\ x_3 – x_1 & y_3 – y_1 \\ \end{array} \right| = \left(x_2 – x_1 \right) \left( y_3 – y_1\right) – \left( x_3 – x_1\right) \left( y_2 – y_1\right)$$ ou seja, $$ \text{área de ABC} = \frac{1}{2}  \text{área de ABCD} = \frac{1}{2} | \alpha \delta – \beta \gamma | = \frac{1}{2} \left| \left(x_2 – x_1 \right) \left( y_3 – y_1\right) – \left( x_3 – x_1\right) \left( y_2 – y_1\right) \right|.$$

Expandindo o determinante temos que $$ \left(x_2 – x_1 \right) \left( y_3 – y_1\right) – \left( x_3 – x_1\right) \left( y_2 – y_1\right) = x_1y_2 + x_2y_3 + x_3 y_1 – x_2y_1-x_3y_2-x_1y_3$$ que é exatamente o deteminante dado por $$ D = \left|\begin{array}{cccc} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{array} \right|$$ Portanto, $$ \text{área de ABC} = \frac{1}{2} |D|, \qquad \text{onde } D = \left|\begin{array}{cccc} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{array} \right|.$$

EXEMPLO: A área do triângulo ABC , cujos vértices são A\left(2,1\right) , B\left( 4,3\right) e C\left( 3,5\right) é igual a $$\text{área de ABC} = \frac{1}{2} \left|\begin{array}{cccc} 2 & 1 & 1\\4 & 3 & 1\\ 3 & 5 & 1 \end{array} \right| = \frac{1}{2} | 6+20+3-4-9-10 | = 3.$$ Com esta área, e colocando a base do triângulo como o segmento \overline{AB} = | \vec{AB}| = \sqrt{(4-2)^2 +(3-1)^2} = 2 \sqrt{2}, concluímos que a altura do triângulo ABC relativa à base \overline{AB} é $$ h = \frac{2 \times \text{área de ABC}}{ | \vec{AB}| } = \frac{6}{2 \sqrt{2}} = \frac{3 \sqrt{2}}{2}.$$

Leia Mais Sobre Vetores no Plano:

• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• O que é um Vetor? Um guia ilustrado dos vetores no espaço.
• O Espaço R²: Coordenadas no Plano Cartesiano
• Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió