Curvas no Espaço | Parametrização de Curvas Clássicas

Uma função vetorial é, por muitas vezes, denominada de curva, pois a representação dada por \vec{F}(t) = x(t) \vec{i} + y(t) \vec{j} + z(t) \vec{k} é chamada de representação paramétrica da curva C, que é a imagem da função vetorial, e t é chamado de parâmetro desta representação. Este tipo de representação é útil em várias aplicações, por exemplo, em mecânica on a variável t pode ser o tempo.

Neste artigo, queremos apresentar a parametrizações das principais curvas estudadas no cálculo e na física. Outras formas de representar curvas no espaço são $$ \tag{1} \left\{ \begin{array}{lll} y & = & f(x) \\ z & = & g(x) \end{array} \right. $$ ou $$ \tag{2} \left\{ \begin{array}{lll} F(x,y,z) & = & 0 \\ G(x,y,z) & = & 0 \end{array} \right.$$ Na forma (2) de escrever uma curva, cada equação representa uma superfície, e a curva é a interseção destas duas superfícies.

Parametrização de uma Reta

Uma reta r com equações paramétricas x(t) = x_1 +at;\;\;y(t) = y_1 +bt e z(t) = z_1 +ct, ou seja, que passa pelo ponto (x_1, y_1, z_1) na direção do vetor (a,b,c) é uma curva parametrizada no espaço \mathbb{R}^3.

Parametrização de uma Circunferência:

Um circunferência C com centro em (0, 0) e raio r>0 é uma curva parametrizada como equações paramétricas dadas por $$x(t) = r cost\;\;\;\;y(t) = r \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$

Se a circunferência não está centrada na origem, mas no ponto (x_0, y_0) e ainda com raio r>0, então sua parametrização será dada por $$x(t) = x_0 + r cost\;\;\;\;y(t) = y_0 + r \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$

Parametrização de uma Elipse

Vamos parametrizar a elipse dada por $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$ Inspirados pela relação $$\cos^2{t}+\sin^2{t}=1$$ temos que
\begin{eqnarray}
x & = & a\cos{t}\\
y & = & b\sin{t} \;\;\;\;\;\;\;\;\;\;\;\;\;t\in[0,2\pi]
\end{eqnarray}

Analogamente ao que fizemos com a circunferência, se a elipse não está centrada na origem, mas no ponto (x_0, y_0) e ainda tem seus eixos na direção dos eixos coordenados, então sua parametrização será dada por $$x(t) = x_0 + a cost\;\;\;\;y(t) = y_0 + b \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$

Parametrização de uma Hipérbole

Vamos parametrizar a hipérbole dada por $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$$ Essa hipérbole possui centro na origem e eixos sobre os eixos coordenados. Inspirados pela relação $$\sec^2{t}-\tan^2{t}=1$$ temos que
\begin{eqnarray}
x & = & a\sec{t}\\
y & = & b\tan{t}
\end{eqnarray}

Parametrização de uma Hélice Circular

A hélice circular é uma curva reversa que se desenvolve sobre a superfície cilíndrica $$x^2 +y^2 = a^2,$$ partindo do ponto (a, 0, 0) e subindo com uma inclinação 0< \theta < 2 \pi , como ilustrado na figura abaixo:

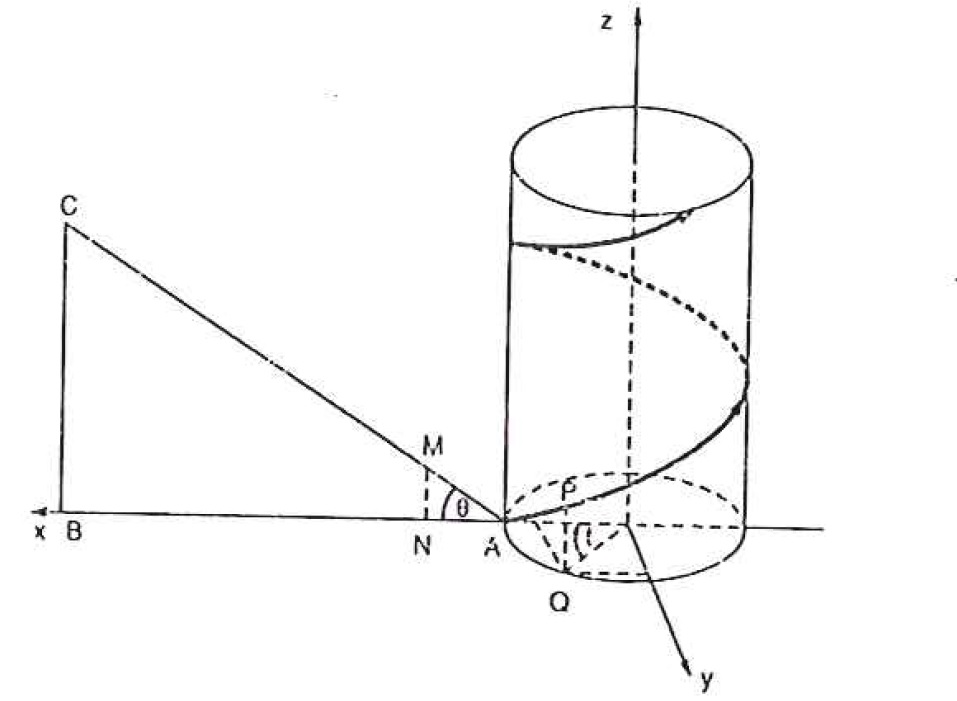
A parametrização desta curva reversa é dada por $$ \vec{r} (t) = acos(t) \vec{i}+ asen(t) \vec{j} + a.t. tg( \theta ) \vec{k}.$$

Parametrização de uma Ciclóide

A ciclóide é uma curva que surgiu para solucionar dois problemas famosos:

• A determinação da formade um cabo, de um ponto A a um ponto abaixo B, como na figura, tal que a bolinha sem atrito, solta em um ponto P entre A e B sobre o cabo, gaste o tempo para alcançar B, qualquer que seja a posição de P.
• A determinação de um único cabo que ligue A a B, ao longo do qual uma bolinha escorregará de A a B no menor tempo possível.

Esses problemas são resolvidos, considerando-se o cabo com a forma de meio-arco de uma ciclóide.

A ciclóide pode ser descrita pelo movimento do ponto P(0,0) de um círculo de raio a, centrado em (0,a), quando o círculo gira sobre o eixo Ox, conforme a figura abaixo:

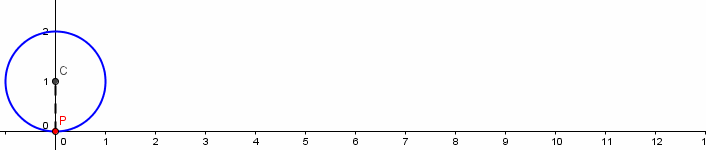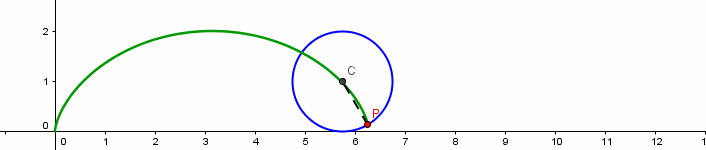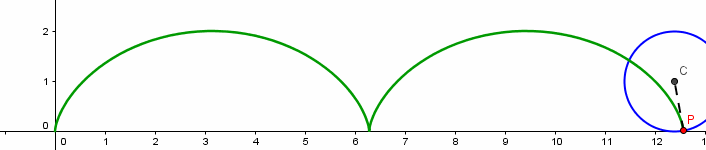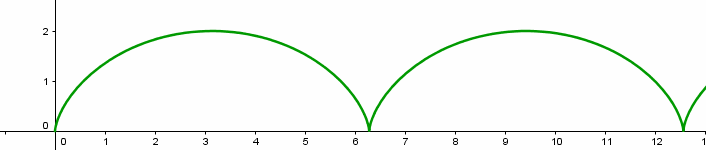
A equação vetorial da ciclóide é dada por

$$\vec{f}(t) = a(t-sen(t)) \vec{i} + a (1-cos(t)) \vec{j}$$ e quando t varia de 0\leq \theta \leq 2 \pi , obtemos o primeiro arco da ciclóide.

Parametrização de de uma Hipociclóide

A hipociclóide é uma é uma curva descrita  pelo movimento de um ponto fixo P, de um círculo de raio b, que gira dentro de um círculo fixo de raio a, a>b.

Essa curva pode ser representada como abaixo:

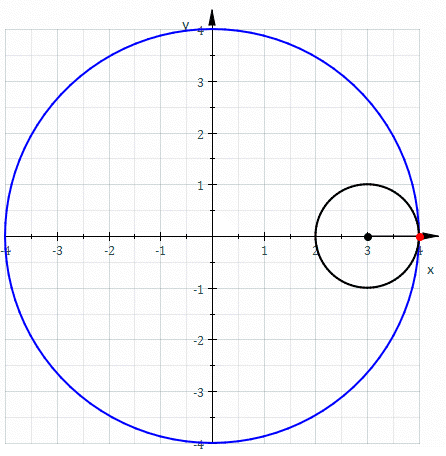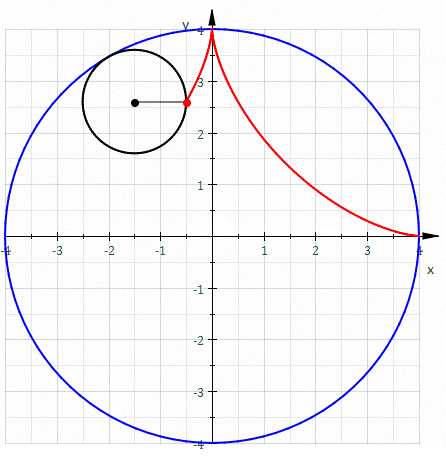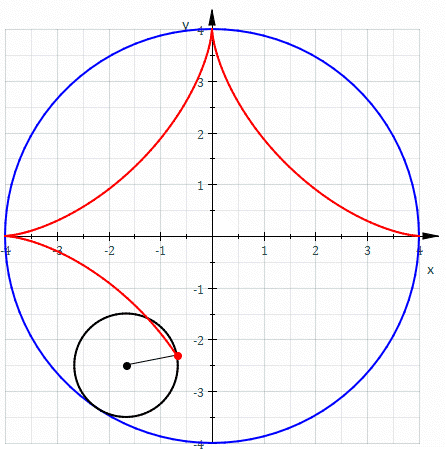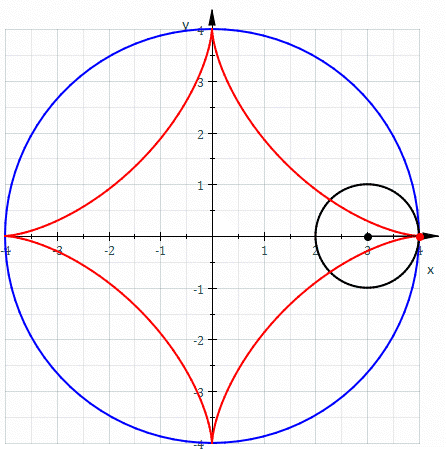
Os pontos onde o ponto de tangência dos dois círculos é o ponto P são chamados de cúspides. Um caso particular muito usado é o da hipociclóide de quatro cúspides, como na imagem.

No caso geral, a equação vetorial da hipociclóide é dada por $$\vec{r}(t) = \left[ (a-b)cos(t) + bcos \left(\frac{a-b}{b} t \right) \right] \vec{i} + \left[ (a-b)sen(t) – bsen \left(\frac{a-b}{b} t \right) \right] \vec{j} $$

No caso particular da hipociclóide de quatro cúspides, a parametrização se reduz a $$\vec{r}(t) = acos^3 (t) \vec{i} + a sen^3 (t) \vec{j}, t \in [0, 2 \pi].$$

Folium de Descartes:

O folium de Descartes é uma curva plana proposta por Descartes para desafiar as técnicas de extremos de Fermat. Na forma paramétrica, esta curva é parametrizada por $$\vec{r}(t)= \frac{3at}{1 + t^3} \vec{i} + \frac{3at^2}{1 + t^3} \vec{j} .$$

Esse fólio foi discutido pela primeira vez por Descartes em 1638 , mas, embora ele tenha encontrado a forma correta da curva no quadrante positivo, ele acreditava que essa forma de folha se repetia em cada quadrante como as quatro pétalas de uma flor.

O fólio tem equação cartesiana dada por x^3 + y^3 = 3axy e uma assíntota de equação dada por x + y + a =0 .

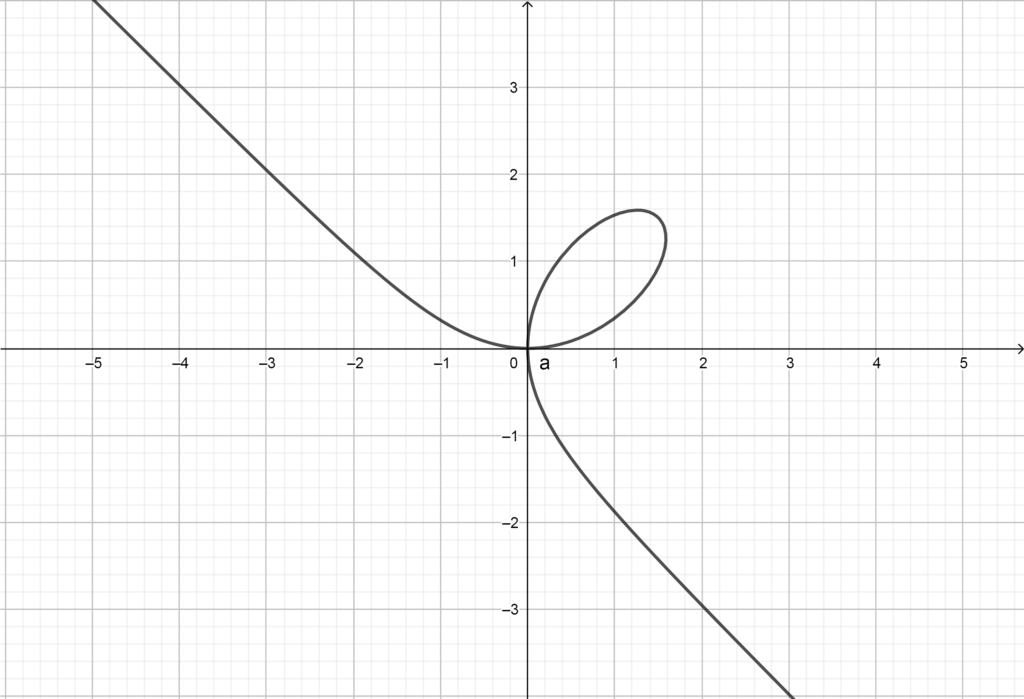
Observe que $$\lim_{t \rightarrow \infty}{\vec{r}(t)} = \vec{i} \lim_{t \rightarrow \infty}{\frac{3at}{1 + t^3}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3at^2}{1 + t^3}} = (0,0), $$ ou seja, quando o parâmetro tender a \pm \infty o fólio tenderá novamente à origem.

EXEMPLO:

Escreva a parametrização da curva y = 5x+3 sobre o plano z = 2.

Observe que essa curva plana é uma reta sobre o plano z=2 . Desta forma, fazendo x = t obtemos $$x(t) = t$$ $$y(t) = 5t +3\;\;\;e$$ $$z(t) = 2.$$

EXEMPLO:

Encontre a parametrização da curva interseção entre as superfícies z=x^2 + y^2 e z=2 +y.

Para encontrar a interseção entre duas superfícies basta igualar as duas equações:

$$ x^2 + y^2 =2 +y \Rightarrow x^2 + y^2 – y=2 \Rightarrow x^2 +(y-1/2)^2 = 9/4,$$

nos dando uma circunferência centrada no ponto (0, 1/2) e raio igual a 3/2.

Logo, temos que $$ x (t) = 3/2 cos (t)$$ $$y (t) = 1/2 + 3/2 sen(t) $$ $$z (t) = ?$$

Para descobrir a função componente z(t) basta substituir y(t) na equação z=2 +y. , encontrando z(t) = 5/2+3/2sen(t) .

Portanto, a parametrização procurada é dada por

$$\vec{r} (t) = [3/2 cos (t)] \vec{i} + [1/2 + 3/2 sen(t)] \vec{j} + [5/2+3/2sen(t)] \vec{k}.$$

EXEMPLO

Obtenha a parametrização da circunferência $$x^2  + y^2 -6x – 4y +4 = 0 $$ no plano z=3.

Usando o completamento de quadrados na equação da circunferência, obtemos

$$(x^2 – 6x +9) + (y^2 – 4y +4) = 9 \Rightarrow $$ $$ \Rightarrow  (x-3)^2 + (y-2)^2 = 3^2,$$ ou seja, temos uma circunferência centrada no ponto (3,2) e com raio R = 3.

Usando a parametrização da circunferência chegamos às funções paramétricas:  $$ \vec{r} (t) = [3+3cos(t)] \vec{i} + [2+3sent] \vec{j} + 3\vec{k}.$$

Leia Mais:

• Curvas no Espaço | Operações Elementares de Funções Vetoriais
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Curvas | Limite e Continuidade de uma Função Vetorial
• Curvas no Espaço | 1ª Lista de Exercícios Resolvidos

Assista nossa Vídeo-Aula: