PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Se você está estudando parábolas como uma curva gerada por seções cônicas e tendo problemas, não se preocupe! Este artigo oferecerá explicações claras para ajudá-lo a compreender este tópico complexo.

Se você está estudando seções cônicas, pode estar tendo trabalho para entender as parábolas. Estas curvas têm propriedades únicas que as tornam importantes em matemática e física. Neste guia, detalharemos os fundamentos das parábolas e forneceremos explicações para ajudá-lo a dominar este tópico.
O que são seções cônicas?
As seções cônicas são as curvas que resultam da interseção de um plano e um cone. O cone pode ser um cone circular reto ou um cone oblíquo. As curvas resultantes são classificadas em quatro tipos: círculos, elipses, parábolas e hipérboles. Cada tipo de curva tem suas próprias propriedades e aplicações únicas em matemática e física. As parábolas, em particular, têm uma propriedade foco-diretriz que as torna úteis em óptica e comunicação por satélite.

O que é uma parábola e como ela é definida?
Uma parábola é um tipo de seção cônica definida como o conjunto de todos os pontos em um plano que são equidistantes de um ponto fixo (chamado de foco) e uma linha fixa (chamada de diretriz). A forma de uma parábola é semelhante à de uma curva em forma de U, com o vértice sendo o ponto mais baixo ou mais alto da curva, dependendo de sua orientação. O foco e a diretriz de uma parábola estão localizados no eixo de simetria, que é uma linha que divide a parábola em duas metades iguais.
| Os livros usados como referência deste artigo sobre a Parábola no Plano são dados abaixo: | ||
Construindo uma Parábola
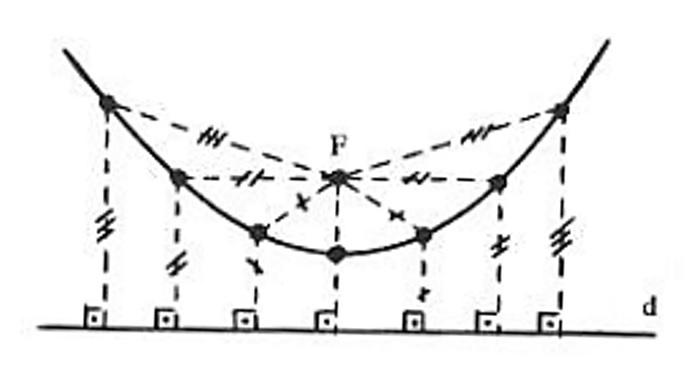
Consideremos no plano uma reta d e um ponto F não pertencente a d . A parábola é o lugar geométrico dos pontos do plano que são eqüidistantes de F e d como ilustrado abaixo. Sendo P' o pé da perpendicular baixada de um ponto P do plano sobre a reta d , de acordo com a definição acima, P pertence à parábola se, e somente se: $$ d(P,F) = d(P,P’) $$ ou ainda $$\left| \vec{PF} \right| = \left| \vec{PP’} \right| .$$
| 
|
OBSERVAÇÃO: Consideramos o fato de F \notin d , pois, caso contrário, a parábola se degeneraria numa reta.
Elementos de Um Parábola
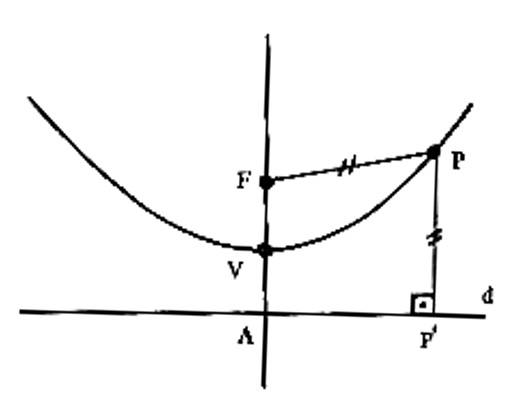
Considerando a figura abaixo, temos:

- Foco: o ponto F ;
- Diretriz: é a reta d ;
- Eixo: é a reta que passa pelo foco e é perpendicular à diretriz;
- Vértice: é o ponto V de interseção da parábola com o seu eixo.
Obviamente, tem de $$ d(V,F) = d(V,A).$$ Com a finalidade de obtermos uma equação da parábola, teremos que referi-la ao sistema de eixos cartesianos.
A Equação da Parábola – O Caso mais Simples: vértice na origem do sistema
Consideraremos a parábola de foco F e diretriz d , que é o conjunto dos pontos P que são equidistantes do ponto F e a reta d .
Eixo da parábola é o eixo Oy:
É usual escolher um sistema de eixos coordenados no qual F\left( 0 , \dfrac{p}{2}\right) e d como a reta horizontal de equação y = - \dfrac{p}{2} (a distância p entre F e a reta d é chamada de parâmetro da parábola). Neste sistema, a parábola contém a origem e é simétrica em relação ao eixo vertical Oy.
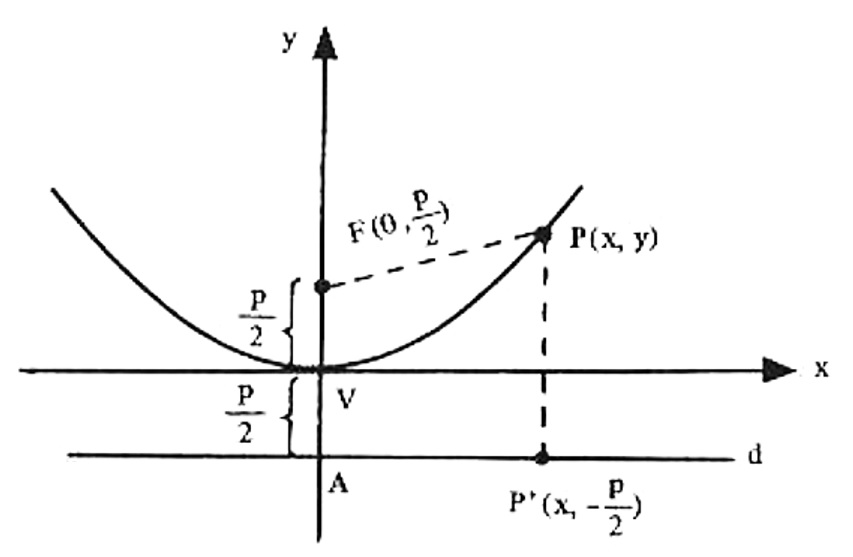
A distância de P à d é dada por \left| y + \dfrac{p}{2} \right| , enquanto a distância de P a F é \sqrt{(x-0)^2 + \left( y - \dfrac{p}{2}\right)^2} . Logo, a equação da parábola é $$ \sqrt{x^2 + \left( y – \frac{p}{2}\right)^2} = \left| y + \frac{p}{2} \right|.$$ Elevando ao quadrado, obtemos $$ x^2 + y^2 – py + \frac{p^2}{4} = y^2 +py + \frac{p^2}{4} $$ e finalmente $$ y = \frac{1}{2p} x^2. \Leftrightarrow x^2 = 2p y$$
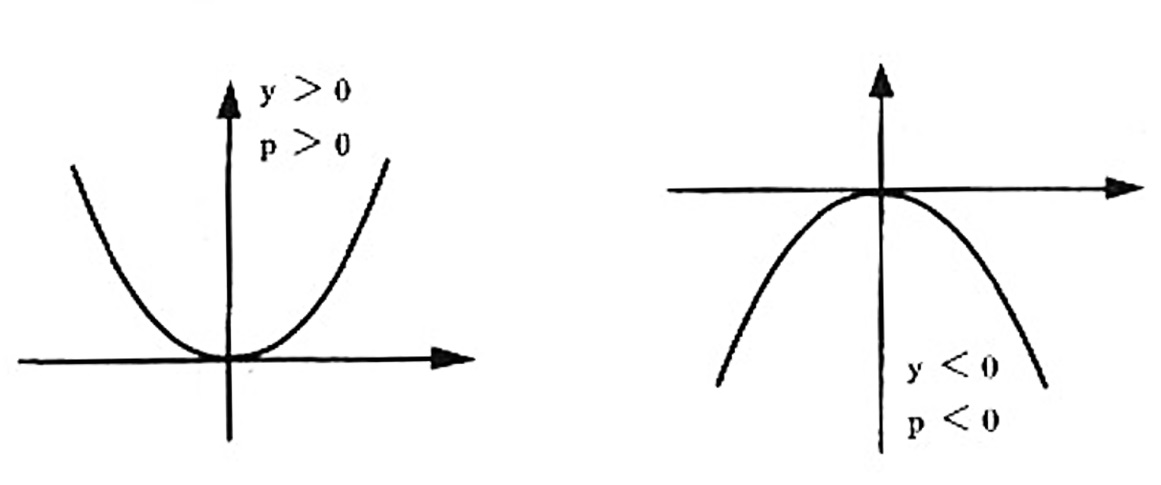
Esta equação é chamada de equação reduzida da parábola e constitui a forma padrão da equação da prábola de vértice na origem tendo para eixo o eixo Oy . Da análise desta equação conslui-se que, tendo em vista ser 2py sempre positivo ou nulo (pois é igual a x^2 \geq 0 ), os sinais de p e de y são sempre iguais. Consequentemente, se p>0 a parábola tem concavidade para cima e, se p < 0 , a parábola tem concavidade para baixo, conforme aas figuras abaixo descrevem:
Eixo da parábola é o eixo Ox:
Sendo P(x,y) um ponto qualquer da parábola de foco F\left( \dfrac{p}{2} , 0\right) e d como a reta vertical de equação x = - \dfrac{p}{2} . Neste sistema, a parábola contém a origem e é simétrica em relação ao eixo horizontal Ox e, de forma análoga ao caso anterior, a equação reduzida será dada por $$ y^2 = 2p x .$$
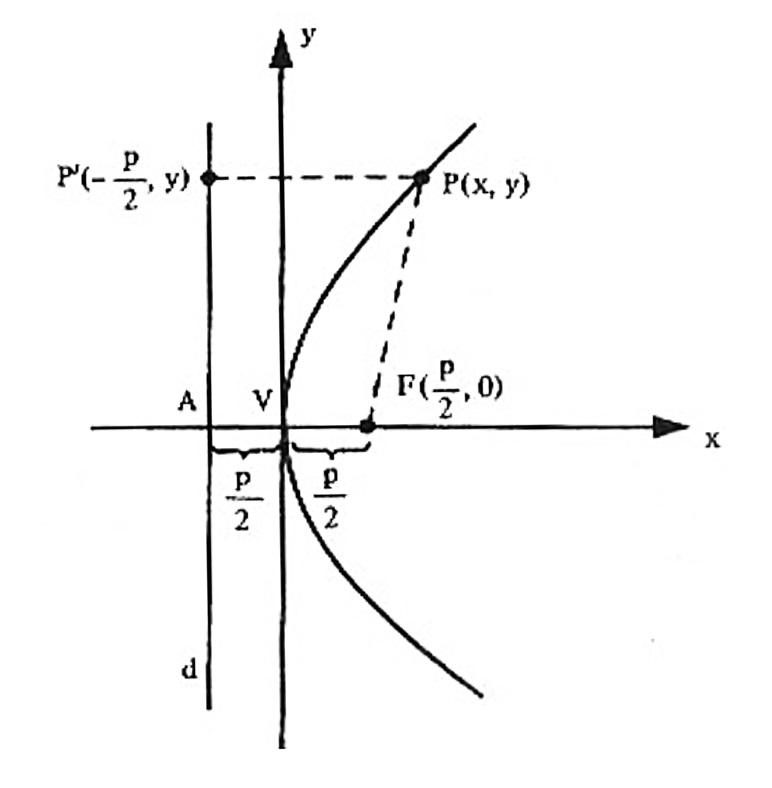
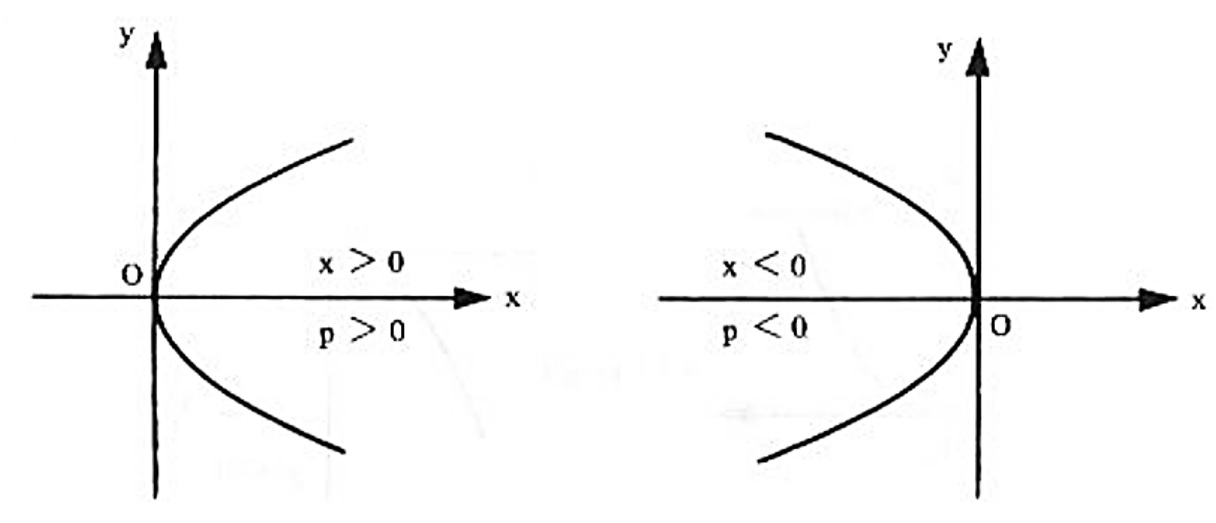
Conforme o sinal de p , teremos: se p>0 a parábola tem concavidade para a direita e, se p < 0 , a parábola tem concavidade para a esquerda.
Equação da Parábola: A Translação de Eixos
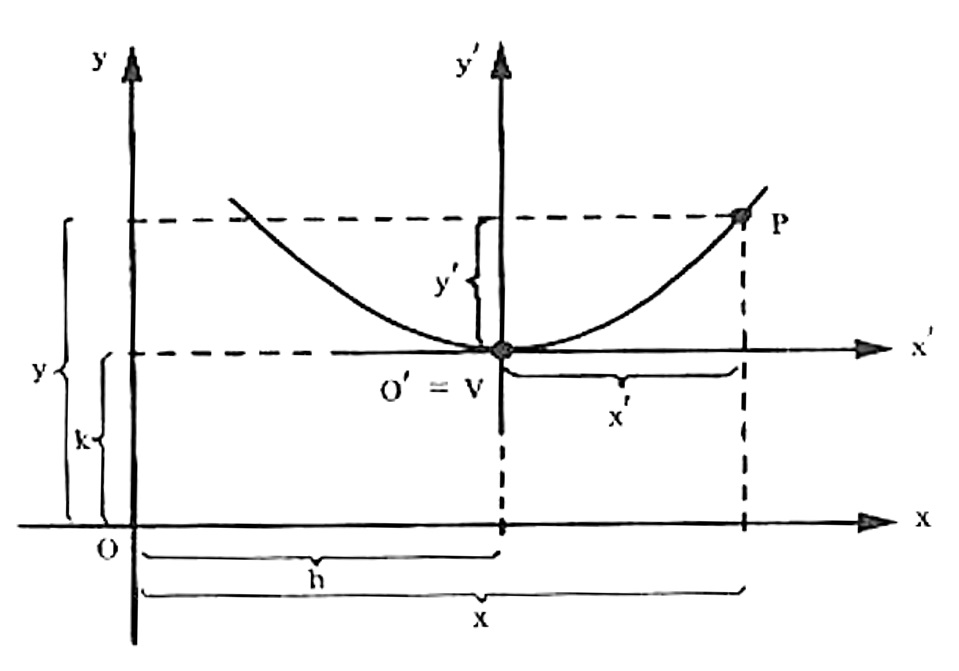
Consideremos no plano cartesiano xOy num ponto O'(h,k) , arbitrário. Vamos introduzir um novo sistema x'Oy' tal que os eixos Ox' e Oy' tenham a mesma unidade de medida, a mesma direção e o mesmo sentido dos eixos Ox e Oy . Nesta condições, um sistema pode ser obtido do outro, através de uma translação de eixos.

Seja P um ponto qualquer do plano tal que suas coordenadas são:
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
- x e y em relação ao sistema xOy ;
- x' e y' em relação ao sistema x'Oy' ;
Pela figura acima, obtem-se $$ x = x’ + h \qquad y = y’+k$$ ou $$ x’ = x-h \qquad y’ = y – k $$ que são as formas de translação e que permitem transformar coordenadas de uma siste ma para outro, sendo que, a principal finalidade da transformação de coordenadas é modificar a forma de equações.
A Equação da Parábola de Vértices Fora da Origem do Sistema
1º Caso: O eixo da parábola é paralelo ao eixo dos y: Seja uma parábola de vértice V(h,k) e eixo paralelo ao eixo dos y , sendo h e k coordenadas de V em relação ao sistema xOy . Seja P(x,y) um ponto qualquer da parábola. Considerando um novo sistema x'Oy' é $$x’^2 = 2p y’$$ mas, como $$ x’ = x-h \qquad y’ = y – k $$ então a equação da parábola com centro em V(h,k) e eixo paralelo ao eixo dos y é dada por $$(x-h)^2 = 2p (y-k)$$ e chamada de forma padrão da equação da parábola.
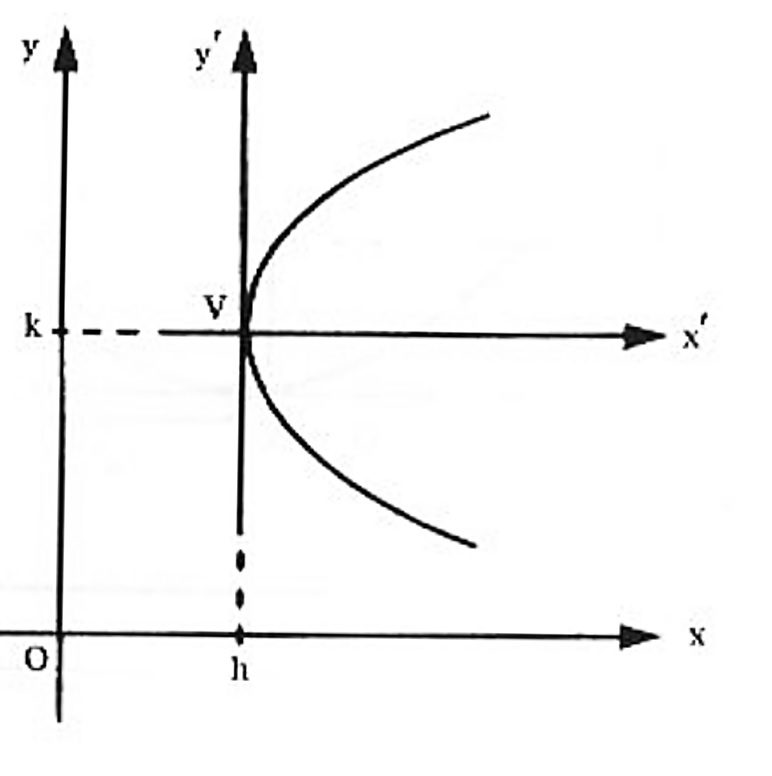
2º Caso: O eixo da parábola é paralelo ao eixo dos x: De modo análogo ao caso anterior, teremos: $$(y-k)^2 = 2p (x – h).$$
A Forma Explícita da Equação da Parábola
Uma equação na forma padrão dada por $$(x-h)^2 = 2p (y-k)$$ pode ser apresentada na forma $$ y = ax^2 +bx+c $$ que é chamada forma explícita da equação da parábola cujo eixo é paralelo ao eixo Oy . Reciprocamente, dada uma equação na forma explícita, podemos sempre conduzí-la à forma padrão. Consequentemente, o gráfico de $$ y = ax^2 + bx + c $$ com a \neq 0 , é sempre uma parábola de eixo paralelo ao eixo dos y . Quando a equação da parábola estiver na forma explícita $$y = ax^2 + bx +c [/katex], a determinação do vértice V(h,k) poderá ser feita com maior rapidez lembrando que h = - \dfrac{b}{2a} .
Se a parábola tem eixo paralelo ao eixo dos x , sua equação na forma explícita é $$ x = a y^2 + by +c $$ correspondente à forma padrão: $$(y-k)^2 = 2p(x-h) .$$ Um detalhe importante na comparação destas equações é que o sinal do coeficientes a é o mesmo de p , e, portanto, a concavidade da parábola fica declarada quando sua equação estiver na forma explícita.
