O Espaço R²: Coordenadas no Plano Cartesiano

Indica-se como $\mathbb{R} ^2$ o conjunto formado pelos pares ordenados $(x,y)$ , onde $x$ e $y$ são números reais. Entenda como este conjunto se relaciona com o plano cartesiano.

Dados $(x,y)$ e $(x' , y' )$ em $\mathbb{R} ^2$ , tem-se que $(x,y) = (x' , y' )$ se, e somente se, $x = x'$ e $y = y'$ . O número $x$ se chama a primeira coordenada e o número $y$ a segunda coordenada do para $(x,y)$ .

Um sistema de eixos ortogonais num plano $\pi$ é um par de eixos $Ox$ e $Oy$ , tomados em $\pi$ , que são perpendiculares e têm a mesma origem $O$ . Diz-se que o eixo $Ox$ é horizontal e o eixo $Oy$ é vertical.

Plano cartesiano - sistema de coordenadas ortogonais plano cartesiano — **Sistema de eixos coordenados no plano.**

Um plano $\pi$ munido de um sistema de eixos ortogonais põe-se, de modo natural, em correspondência biunívoca com o conjunto $\mathbb{R} ^2$ . Dado o ponto $P$ do plano, baixamos por ele paralelas aos eixos $Ox$ e $Oy$ . Estas retas paralelas cortam os eixos em pontos cijas coordenadas são $x$ e $y$ respectivamente.

Ao ponto $P$ do plano $\pi$ faz-se corresponder o par ordenado $(x,y) \in \mathbb{R} ^2$ . Reciprocamente, a cada par ordenado $(x,y) \in \mathbb{R} ^2$ corresponde a um ponto $P \in \pi$ . Os números $x$ e $y$ chama-se coordenadas cartesianas do ponto $P$ relativamente ao sistema de eixos ortogonais fixado: $x$ é a abcissa e $y$ a ordenada de $P$ .

Em todo o nosso estudo sobre geometria analítica, a menos que seja feita explicitamente uma menção em contrário, admitiremos que foi fixado um sistema de eixos ortogonais no plano, que assim se identifica a $\mathbb{R} ^2$ . Cada ponto $P(x,y)$ do plano passa a ser a mesma coisa que um par ordenado de números reais.

Os eixos ortogonais decompões o plano em quatro regiões, chamados quadrantes. Tem-se o primeiro quadrante, formado pelos pontos que têm ambas coordenadas positivas. No segundo quadrante, a abcissa é negatica e a ordenada é positiva. No terceiro quadrante, abcissa e ordenada são ambas negativas. No quarto quadrante, os pontos têm abcissa positiva e ordenada negativa.

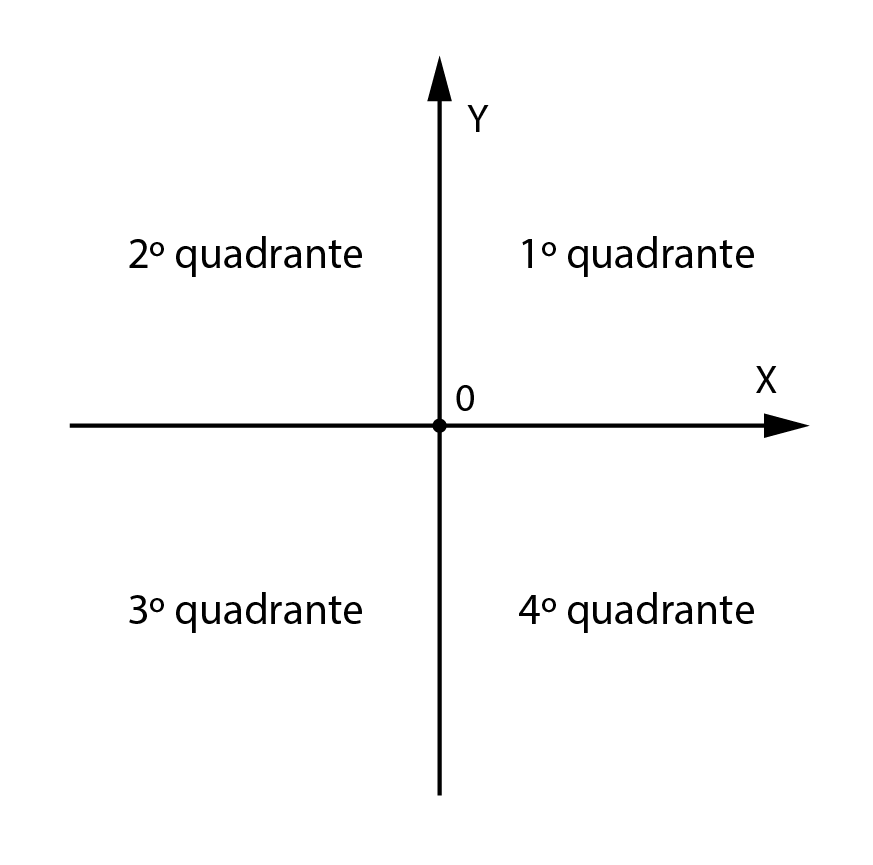
Evidentemente, os pntos do eixo $Ox$ das abcissas têm coordenadas $(x,0)$ e no eixo das ordenadas $Oy$ os pontos são da forma $(0,y)$ . O ponto $O$ , origem dos eixos, tem coordenadas $(0,0)$ .

Assista nossa vídeo-aula sobre o espaço $\mathbb{R}^2$ no nosso canal no YouTube – Inscreva-se no canal para ter aulas de matemática gratuitamente!

A Distância Entre Dois Pontos no Plano Cartesiano

Dados os pontos $P_1 = \left( x_1 , y_1 \right)$ e $P_2 = \left( x_2 , y_2 \right)$ , queremos obter a expressão da distância entre estes dois pontos, dada por $d \left( P_1 , P_2 \right)$ em termos das coordenadas de $P_1$ e $P_2$ . Para isso, introduzimos o novo ponto $Q = \left( x_2 , y_1 \right)$ .

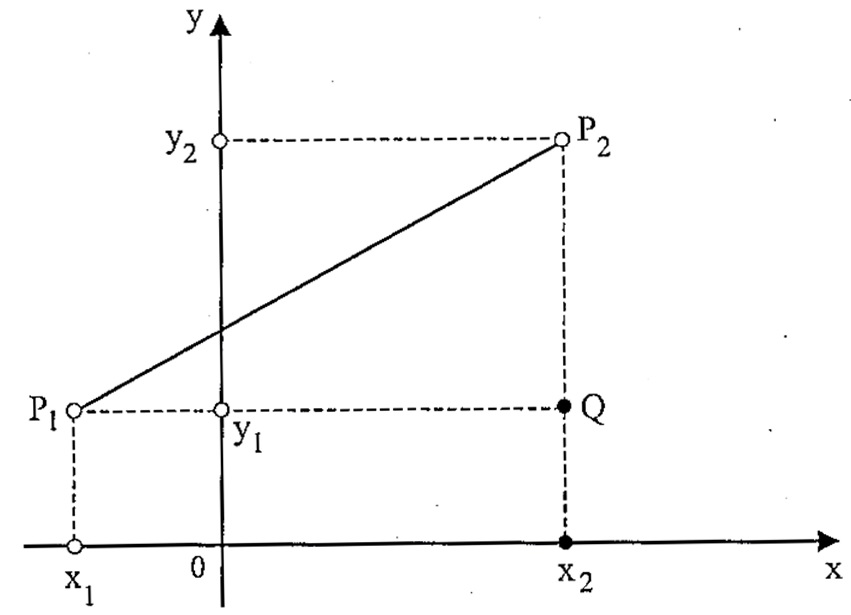
Demonstração da fórmula da distância entre dois pontos — **O triângulo da figura é retângulo e a sua hipotenusa mede exatamente a distância entre os pontos que queremos calcular**

Como $P_1$ e $Q$ têm a mesma ordenada, o segmento $P_1 Q$ é horizontal (paralelo ao eixo $Ox$ ) e mede $| x_1 - x_2 |$ . Analogamente, o segmento $P_2 Q$ é vertical (paralelo ao eixo $Oy$ ) e mede $| y_1 - y_2 |$ . Portanto, $P_1 P_2$ é a hipotenusa do triângulo retângulo $P_1 P_2 Q$ . Do teorema de Pitágoras, temos que $$ d \left( P_1 , P_2 \right) = \sqrt{\left( x_1 – x_2 \right)^2 + \left( y_1 – y_2 \right)^2 }.$$

EXEMPLO: Vamos calcular a distância entre os pontos $A(2,-1)$ e $B(-1,3)$ . Usando a fórmula apresentada anteriormente temos que $$ d \left( A , B \right) = \sqrt{\left( 2 – (-1) \right)^2 + \left(-1-3 \right)^2 } = \sqrt{9+16} = \sqrt{25} = 5.$$

Pode acontecer eventualmente que uma das pacelas do radicando (ou até mesmo duas) seja nula; de fato, para os pontos $A(2,1)$ e $B(2,5)$ , teremos $x_A - x_B = 2-2 = 0.$ Note que o segmento $\overline{AB}$ é vertical e que, portanto, a distância entre estes dois pontos é igual a 4. Em casos como este é conveniente escrever $$d(A,B) = |5-1| = 4 \qquad \text{ou} \qquad d(A,B) = |1-5| = 4.$$

De maneira análoga devemos tratar o segmento horizontal, que aparece quando os pontos possuem a mesma ordenada. É importante salientar que, embora tenhamos deduzido a nossa fórmula usando pontos do 1º quadrante, ela não perde o seu valor quando temos pontos de outros quadrantes, o que poderá ser observado durante a resolução dos exercícios.

O Ponto Médio de Um Segmento

Há muitos problemas em Geometria Analítica que envolvem mediatrizes de segmentos, medianas e mediatrizes de triângulos e outros assuntos relacionados com o ponto médio de um segmento.

Seja $M$ o ponto médio do segmento com extremidades $A \left( x_A , y_A \right)$ e $B \left( x_B , y_B \right)$ . Notemos que os triângulos $AMN$ e $ABP$ são semelhantes, pois possuem os três ângulos respectivamente congruentes, como vemos na imagem abaixo:

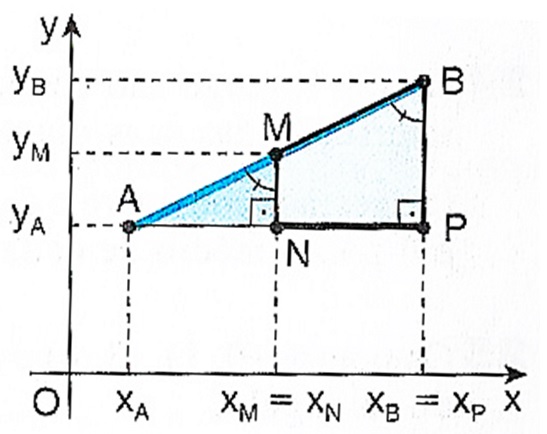
Assim $$ \frac{AM}{AB} = \frac{AN}{AP}.$$ Mas $AB = 2 \times (AM)$ , pois $M$ é o ponto médio de $AB$ . Logo, $$ \frac{AM}{2 \times AM} = \frac{AN}{AP} \Rightarrow \frac{AN}{AP} = \frac{1}{2},$$ donde $AP=2 \times (AN).$ Assim, temos $$ x_P – x_A = 2 \left( x_N – x_A \right) \Rightarrow x_B – x_A = 2 \left( x_M – x_A \right) \Rightarrow x_M = \frac{x_A + x_B}{2} .$$

De forma análoga, prova-se que $$y_M = \frac{y_A + y_B}{2} .$$ Portanto, sendo $M$ o ponto médio do segmento $\overline{AB}$ , temos $$M\left( \frac{x_A + x_B}{2} , \frac{y_A + y_B}{2} \right).$$

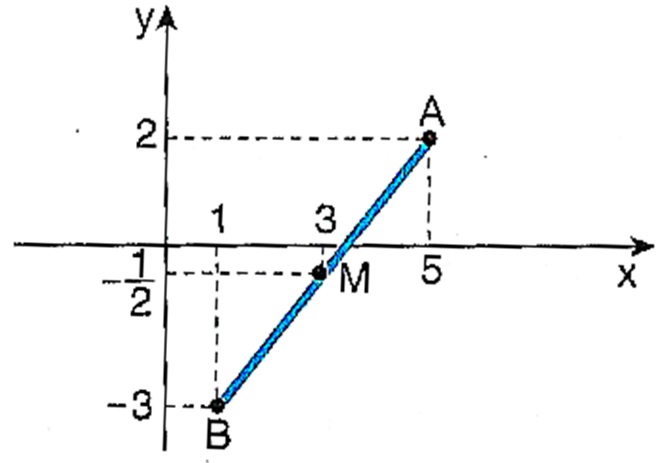
EXEMPLO:

Sendo dados os pontos $A(5,2)$ e $B(1,-3)$ , temos que o ponto médio do segmento $\overline{AB}$ é dado por $$M\left( \frac{5 + 1}{2} , \frac{2 + (-3) }{2} \right) = \left( 3, – \frac{1}{2}\right).$$

Apoie Nosso Trabalho:

Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697

Condição de Alinhamento de Três Pontos

É possível verificarmos se três pontos do plano, distintos dois a dois, estão alinhados. Vamos supor que os pontos $A \left( x_1 , y_1 \right)$ , $B \left( x_2 , y_2 \right)$ e $C \left( x_3 , y_3 \right)$ estejam alinhados como na imagem abaixo:

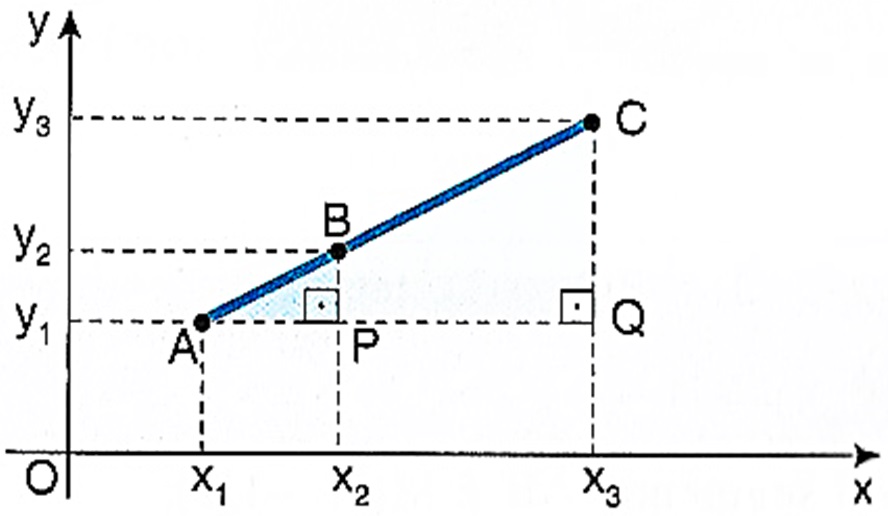
Prolonguemos a reta horizontal que passa por $A$ , obtendo os pontos $P$ e $Q$ , os quais formam os triângulos retângulos $ABP$ e $ACQ$ , que são semelhantes. Decorre que a proporção $$ \frac{AQ}{AP} = \frac{CQ}{BP} ,$$ que pode ser escrita como $$ \frac{ x_{3} – x_{1} }{ x_{2} – x_{1} } = \frac{ y_{3} – y_{1} }{ y_{2} – y_{1} }.$$ Desenvolvendo essa expressão, obtemos: $$ \left( x_{3} – x_{1} \right) \left( y_{2} – y_{1} \right) – \left( x_{2} – x_{1} \right)\left( y_{3} – y_{1} \right) = 0 $$ que pode ser escrita sob a forma $$ \left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right| = 0 .$$

Assim, para constatar a colinearidade de três pontos, basta calcularmos um detrminante de terceira ordem que contenha em cada linha a abcissa de um dos pontos dados, a respectiva ordenada e o número 1, mantida essa ordem. Se tal determinante for nulo, e só nesse caso, os pontos estarão alinhados

EXEMPLO:

Para verificar se os pontos $(6,5)$ , $(3,4)$ e $(-3,2)$ são colineares, construímos inicialmente o determinante $$ \left| \begin{array}{ccc} 6 & 5 & 1 \\ 3 & 4 & 1 \\ -3 & 2 & 1 \end{array} \right| = 24-15+6+12-12-15 = 0 .$$ Logo, estes pontos são colineares.

O Espaço R²: Coordenadas no Plano Cartesiano

Indica-se como $\mathbb{R} ^2$ o conjunto formado pelos pares ordenados $(x,y)$ , onde $x$ e $y$ são números reais. Entenda como este conjunto se relaciona com o plano cartesiano.