Retas no Plano Cartesiano: Equações Reduzida, Geral, Vetorial e Paramétrica

Para que uma reta fique perfeitamente determinada, basta que tenhamos a sua direção e um ponto por onde ela passe. Neste artigo quero explorar as diferentes equações que uma reta pode ter no plano: geral, reduzida, vetorial e paramétrica.

As figuras geométricas elementares no plano são os pontos e as retas. O plano é constituído de pnto e as retas são subconjuntos distinguidos dos pontos do plano. Pontos e retas do plano satisfazem a cinco grupos de axiomas que sustentam a geometria euclidiana plana. Vamos destacar abaixo os dois primeiros que serão muito importantes para o nosso estudo da reta no plano:

1. AXIOMA 1: Qualquer que seja a reta no plano existem pontos que pertencem e pontos que não pertencem à reta;
2. AXIOMA 2: Dados dois pontos distintos existe uma única reta que os contém; este segundo axioma nos garante que uma reta divide o plano em dois semi-planos cjua interseção é a própria reta.

A Reta no Plano como Gráfico de uma Função Afim

Uma função real f:\mathbb{R} \rightarrow \mathbb{R} dada por f(x) = ax+b, onde a e b são números reais e a\neq 0 é denominada Função Afim. Por vezes ela é também chamada de Função do 1° grau, mas esta referência é errada, pois função não tem grau, polinômio sim. Talvez pela associação com polinômios do primeiro graus está nomenclatura tenha se aplicado. Uma função afim é denominada linear se for do primeiro grau e b=0.

O gráfico de uma função afim é sempre uma reta crescente se a>0 ou uma reta decrescente se a<0. a = \tan{\alpha} é denominado coeficiente angular e b é denominado coeficiente linear. Este resultado é garantido pelo teorema abaixo:

TEOREMA: o gráfico de uma função afim é uma reta não vertical. Reciprocamente, toda reta não-vertical é o gráfico de uma função afim.

Demonstração:  ( \Rightarrow) Para provar que o gráfico de uma função afim f(x) = ax+b é uma reta, basta tomar três pontos quaisquer $$ P_1(x_1 , ax_1 +b ), \qquad P_2 (x_2 , ax_2 +b ), \qquad P_3(x_3 , ax_3 +b )$$ com $$ x_1 < x_2 < x_3 $$ e mostrar que les são colineares. Como vimos neste artigo, três pontos são colineares se $$ \left| \begin{array}{ccc} x_1 & ax_1 +b & 1 \\ x_2 & ax_2 +b & 1 \\ x_3 & ax_3 +b& 1 \end{array} \right| = 0 .$$ Mas este é um resultado é imediato, pois, por propriedades de determinante, temos que $$ \left| \begin{array}{ccc} x_1 & ax_1 +b & 1 \\ x_2 & ax_2 +b & 1 \\ x_3 & ax_3 +b& 1 \end{array} \right| = \left| \begin{array}{ccc} x_1 & ax_1  & 1 \\ x_2 & ax_2 & 1 \\ x_3 & ax_3 & 1 \end{array} \right| + \left| \begin{array}{ccc} x_1 & b & 1 \\ x_2 & b & 1 \\ x_3 & b& 1 \end{array} \right| = 0 + 0 = 0 $$ pois os dois determinantes que obtemos possuem colunas múltiplas.

( \Leftarrow ) Reciprocamente, dada uma reta não vertical r , sua interseção com o eixo Oy é um ponto cuja ordenada chamamos de b . Fixamos um ponto (x_0 , y_0) na reta r , com x_0 \neq 0 , e pomos a = \dfrac{y_0 - b}{x_0} como na figura abaixo.

Afirmamos que a reta r é o gráfico da função afim y = ax+b . De fato, pela ida já mostramos que esse gráfico é uma reta s que passa pelos pontos (x_0 , y_0) e (0 , b) e como r também possui estes dois pontos concluímo que o gráfico de f é r , pois só existe uma única reta passando por dois pontos dados.

Equação Vetorial da Reta no Plano

Seja r uma reta que passa pelo ponto A(x_0 , y_0 ) e tema direção do vetor não nulo \vec{v} = ( \alpha , \beta ) . Para que um ponto P(x,y) do plano pertença à retar r , é necessário e suficiente que os vetores  \vec{AP} = ( x- x_0 , y - y_0 ) e \vec{v} = ( \alpha , \beta ) sejam paralelos, isto é, $$ \vec{AP} = t \vec{v} $$ ou $$ P – A = t \vec{ v } .$$ Da soma de vetores com pontos, sabemos que $$ P = A – t \vec{ v }, \qquad t \in \mathbb{R} .$$ Ou seja, $$ (x,y) = (x_0 , y_0 ) + t ( \alpha , \beta ) , \qquad t \in \mathbb{R} .$$

Qualquer uma das equações acima são chamadas de equações vetoriais da reta r . O vetor \vec{v} = ( \alpha , \beta ) é chamado de vetor diretor da reta y   e t \in \mathbb{R} é chamado de parâmetro. É fácil verificar que a cada valor de t corresponde um ponto particular P : quando t  varia de - \infty a \infty , o ponto P descreve a reta r .

Equações Paramétricas e Geral da Reta no Plano

Seja r uma reta que passa pelo ponto A(x_0 , y_0 ) e tema direção do vetor não nulo \vec{v} = ( \alpha , \beta ) . Sabemos que a equação vetorial da reta r é dada por $$ (x,y) = (x_0 , y_0 ) + t ( \alpha , \beta ) , \qquad t \in \mathbb{R} .$$ Daí, temos que $$ (x,y) = (x_0 + t \alpha , y_0 + t \beta) $$ donde obtemos $$ \left\{ \begin{array}{rrr} x  & = & x_0 + t \alpha \\ & \\ y &= & y_0 + t \beta \\ \end{array} \right. ; \qquad t \in \mathbb{R} .$$ Estas equações são denominadas Equações Paramétricas da reta r .

Das equações paramétricas, supondo o produto \alpha . \beta \neq 0 , temos que $$t = \frac{x – x_0}{ \alpha } = \frac{y – y_0}{\beta} $$ temos que $$ \beta (x – x_0 ) = \alpha (y – y_0 ) \Leftrightarrow \beta x – \alpha y = \beta x_0 – \alpha y_0. $$ Fazendo \beta = a , - \alpha = b e \beta x_0 - \alpha y_0 = c encontramos a equação geral da reta r : $$ ax + by = c.$$

Partindo novamente de $$ \beta (x – x_0 ) = \alpha (y – y_0 ) $$ temos $$ \beta (x – x_0 ) = \alpha (y – y_0 ) \Leftrightarrow \alpha y = \beta x – \beta x_0 + \alpha y_0 \Leftrightarrow y = \frac{\beta}{\alpha} x + \frac{- \beta x_0 + \alpha y_0}{ \alpha}.$$ Fazendo $$ m = \frac{\beta}{\alpha} \qquad \text{ e } \qquad n = \frac{- \beta x_0 + \alpha y_0}{ \alpha}, $$ obtemos a equação reduzida da reta r : $$ y = m x +n $$ sendo m o coeficiente angular e n o coeficiente linear da reta r .

Dados os dois pontos A \left( x_1 , y_1 \right) e B \left( x_2 , y_2 \right) o coeficiente angular da reta que passa por ambos é dado por $$ m = \frac{y_2 – y_1}{x_2 – x_1}.$$

Equação Geral da Reta no Plano Usando Vetores.

Teorema: Os vetores \vec{u} e \vec{v} são perpendiculares se, e somente se, \vec{u} \cdot \vec{v} = 0 .

Uma aplicação deste teorema é a dedução da equação geral da reta usando vetores . Dada uma reta r no plano, seja \vec{n} = (a,b) um vetor normal (ou seja, perpendicular a todo vetor que tenha essa r como reta suporte)  como dado na figura abaixo:

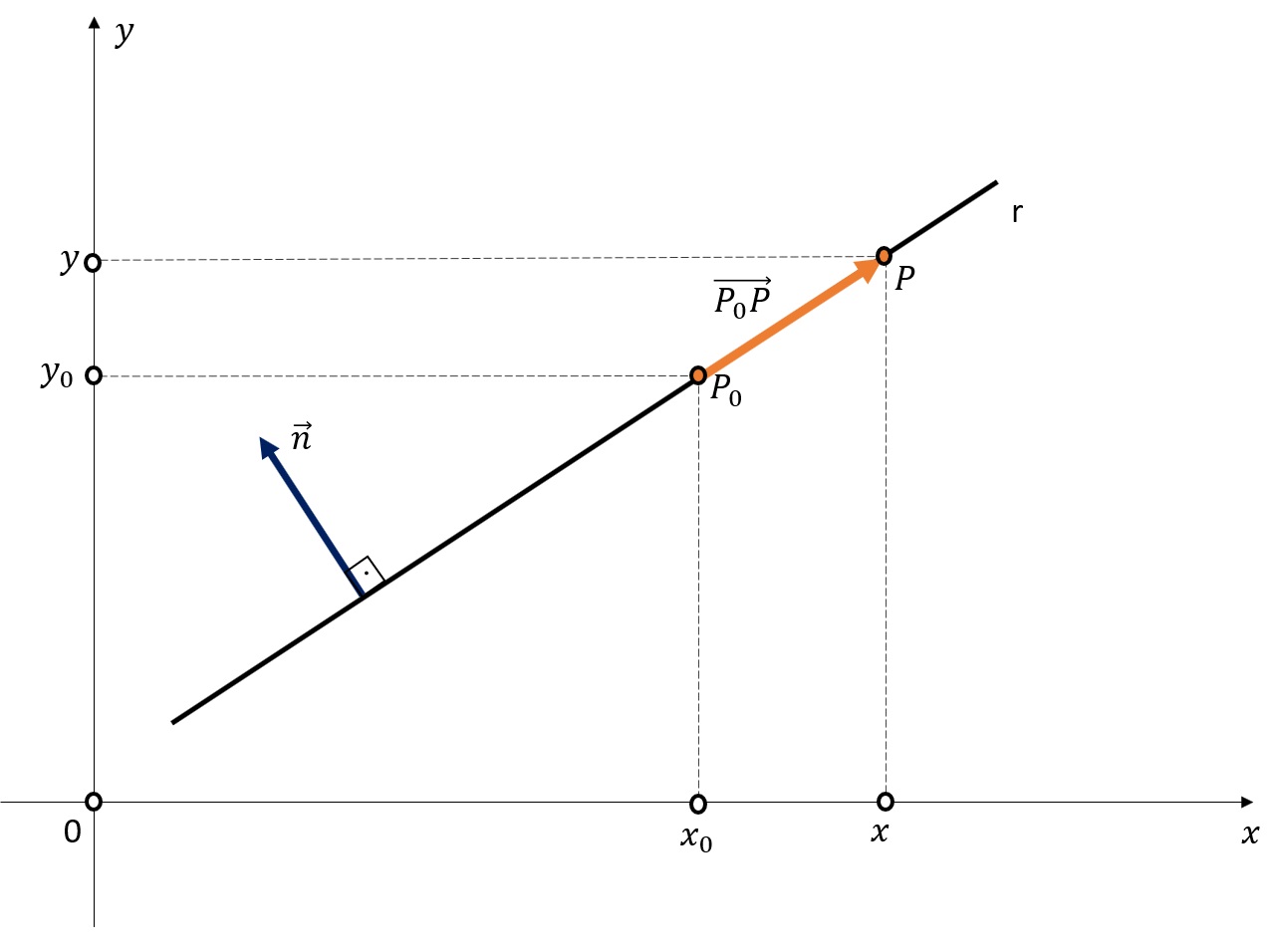
Seja P_0 \left( x_0 , y_0 \right) um ponto fixado na reta r . Um ponto P \left( x , y \right) do plano pertence à reta r se o vetor \vec{P_o P} = \left( x - x_0 ,y-  y_0 \right) é perpendicular ao vetor \vec{n} = (a,b) . Ou seja, se $$ \vec{P_o P} \cdot \vec{n} = 0 \Rightarrow a \left( x – x_0 \right) + b \left( y-  y_0 \right) = 0 \Rightarrow ax +by – \left(  a x_0 + by_0 \right) = 0$$ Fazendo c = \left(  a x_0  + by_0 \right) , encontramos que a equação geral da reta no plano é dada por $$ ax + by = c.$$

A Equação Geral da Reta no Plano determinada por dois pontos

A determinação de uma reta também pode se dar por meio de dois de seus pontos. Sejam A \left( x_1 , y_1 \right) e B \left( x_2 , y_2 \right) . Seja P \left( x , y \right)   um ponto genérico dessa reta. Evidentemente P esta alinhado com os pontos A e B ; vale, pois, a condição de alinhamento: $$ \left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array} \right| = 0 .$$ Resolvendo, temos: $$x_1 y_2+ xy_1 + x_2 y -x y_2 – x_2 y_1 – x_1 y = 0$$ $$ x (y_1 – y_2 )+y(x_2 – x_1) + (x_1 y_2 – x_2 y_1) = 0.$$ Fazendo a =  (y_1 - y_2 ) e b = (x_2 - x_1) e c = x_1 y_2 - x_2 y_1 e teremos $$ ax +by+c = 0, $$ que é chamada de Equação Geral da Reta r . 

Uma outra forma de se encontrar esta equação geral da reta que passa pelos pontos A \left( x_1 , y_1 \right) e B \left( x_2 , y_2 \right) é usando a conhecida fórmula $$ y – y_1 = m \left( x- x_1 \right)$$ onde $$ m = \frac{y_2 –  y_1}{ x_2 – x_1}$$ é o coeficiente angular desta reta.

Leia Mais Sobre Geometria Analítica no Plano:

• Vetores no Plano R²: Norma e Produto Escalar
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• O Espaço R²: Coordenadas no Plano Cartesiano
• O que é um Vetor? Um guia ilustrado dos vetores no espaço.