Retas no Plano Cartesiano: 1ª Lista de Exercícios Resolvidos

Esta lista de exercícios resolvidos é perfeita para você que quer entender as retas (equações e posições relativas) no plano cartesiano através de problemas que irão refinar seu raciocínio lógico em geometria analítica.

As figuras geométricas elementares no plano são os pontos e as retas. O plano é constituído de pnto e as retas são subconjuntos distinguidos dos pontos do plano. Pontos e retas do plano satisfazem a cinco grupos de axiomas que sustentam a geometria euclidiana plana.

Basicamente, duas retas no plano obrigatoriamente devem ser paralelas ou concorrentes. Até por isso, ao definirmos uma reta paralela estaremos definindo automaticamente as retas concorrentes. Desta forma, a distância entre duas retas só faz sentido ser calculada no plano se as retas são paralelas, pois, caso contrário, sendo concorrentes, sua distância é zero, afinal elas possuem um ponto de interseção.

1ª Lista de Exercícios Resolvidos sobre Retas no Plano

1) Determine a equação geral da reta s da figura abaixo. Em seguida, determine o ângulo entre as retas r e s e seu ponto de interseção.

SOLUÇÃO: A reta r passa pelos pontos (-2,3) e (0,-2) , logo, sua equação geral é dada por $$ \left| \begin{array}{ccc} -2 & 3 & 1 \\ 0 & -2 & 1 \\ x & y & 1 \end{array} \right| = 0 .$$ Resolvendo, temos: $$5x+2y+4 = 0$$ Na equação de r , quando y = 0 , temos x= -\frac{4}{5} . Assim, r passa ( e s também) por \left( -\frac{4}{5} , 0\right) . Logo, a equação geral de s é dada por $$ \left| \begin{array}{ccc} -\frac{4}{5} & 0 & 1 \\ 0 & 3 & 1 \\ x & y & 1 \end{array} \right| = 0 \Rightarrow 15x-4y+12 = 0.$$

2) Seja r a reta de equação dada por 2x+3 . Determine a forma geral da equação desta reta e responda:

1. 1. r passa pela origem? Não, pois o coeficiente linear é diferente de zero.
   2. qual é o coeficiente angular de r ?  m =2 ;
   3. quais são pontos em que r corta os eixos cartesianos? A reta r cruza o eixo Oy quando x=0 , logo, (0,3) é o ponto onde a reta cruza o eixo Oy . Em contrapartida, quando y=o a reta r cruza o eixo Ox , no ponto (-3/2,0)
   4. qual o vetor diretor da reta r ?  \vec{v} = (3/2 , 3) ;
   5. qual o vetor normal da reta r ?  \vec{n} = (2,-1) .

3) Encontre a área e o perímetro do triângulo com vértices na origem e nos pontos em que a reta de equação 3x+2y+9 = 0 corta os eixos cartesianos. 

SOLUÇÃO: Primeiramente, vamos encontrar os pontos que a reta cruza os eixos:

• Eixo x: para isso, colocamos y =0 , logo, obtemos 3x+9 = 0 \rightarrow x = -3 . Portanto (-3,0) é um ponto da reta que cruza o eixo x;
• Eixo y: para isso, colocamos x =0 , logo, obtemos 2y+9 = 0 \rightarrow y = \dfrac{-9}{2} . Portanto \left(0, \dfrac{-9}{2} \right ) é um ponto da reta que cruza o eixo y.

Logo, o triângulo é formado pelos pontos O(0,0) , A (-3,0) e B \left(0, \dfrac{-9}{2} \right) cujo perímetro é dado por $$ | \vec{OA} | + | \vec{OB} | + | \vec{AB} | = \\ = | (-3,0) | + \left| \left(0, \frac{-9}{2} \right) \right| + \left| \left(3, \frac{-9}{2} \right) \right| = \\ = 3 + \frac{9}{2} + \sqrt{ 9 + \frac{81}{4} } = 3 + \frac{9}{2} + \sqrt{ \frac{117}{4} } = \frac{15}{2} + \sqrt{ \frac{117}{4} } = \frac{15+ 3 \sqrt{13}}{2}$$

4) A reta que passa por A(1,-2) e B(-2,4) intersepta em P a reta s que, além de passar por C(4,0) , forma com os eixos coordenados um triângulo retângulo isósceles. Determine as coordenadas do ponto P .

SOLUÇÃO: Inicialmente chamemos de r a reta que passa por A e B e determinemos sua equação ( y = mx +n  ) através do sistema $$ -2 = m + n \\ 4 = -2m + n $$ que fornece m = -2  e n = 0 . Assim r é dada pela equação y = -2x . Por outro lado, coo forma com os eixos um triângulo isósceles no 4º quadrante, s corta o eixo y no ponto de ordenada -4 , a qual nos fornece o valor de n: n=-4 . Para determinarmos m , basta aplicarmos à equação y = mx + n as coordenadas do ponto C : $$ 0 = 4m +n \Rightarrow 0 = 4m – 4 \Rightarrow m = 1.$$ Temos, então $$ r: y = -2x \\ s: y = x-4. $$ Resolvendo o sistema obtido, temos $$x_P = \frac{4}{3}, \qquad y_P = \frac{-8}{3}$$ ou seja, P \left( \dfrac{4}{3} , -\dfrac{8}{3} \right) é o ponto procurado.

5) Seja a reta r dada por y = 2x-1 . Escreva as equações da reta s que passa por P(1,4) de modo que r // s .

SOLUÇÃO: Seja a reta r dada por y = 2x-1 . Pelo ponto P(1,4) , fora de r , vamos traçar a reta s , de modo que r // s . Para que r // s , é necessário que m_s = m_r = 2 . Assim, podemos escrever $$ s: y = 2x +n.$$ Como P \in s , temos $$ 4 = 2 \cdot 1 + n \Rightarrow n = 2 $$ e finalmente $$ s: y = 2x+2$$ é a equação da reta paralela a r traçada por P .

6)Encontre a equação da reta s , perpendicular a r: 2x+1, traçada pelo ponto A(5,0) .

SOLUÇÃO: Para achar a equaçao da reta s , perpendicular a r: 2x+1, traçada pelo ponto A(5,0) , devemos calcular inicialmente m_s : $$ r \perp s \Rightarrow m_s = – \frac{1}{m_r} = – \frac{1}{2}.$$ Como s por P(5,0) , podemos escrever: $$ y – 0 = – \frac{1}{2}(x-5) \qquad \text{e} \qquad y = – \frac{1}{2}x + \frac{5}{2} $$ ou $$ s: x + 2y – 5 = 0, $$ que é a equação da reta procurada.

7) O triângulo ABC da figura abaixo é equilátero. Determine a equação da reta suporte ao lado \overline{AC} .

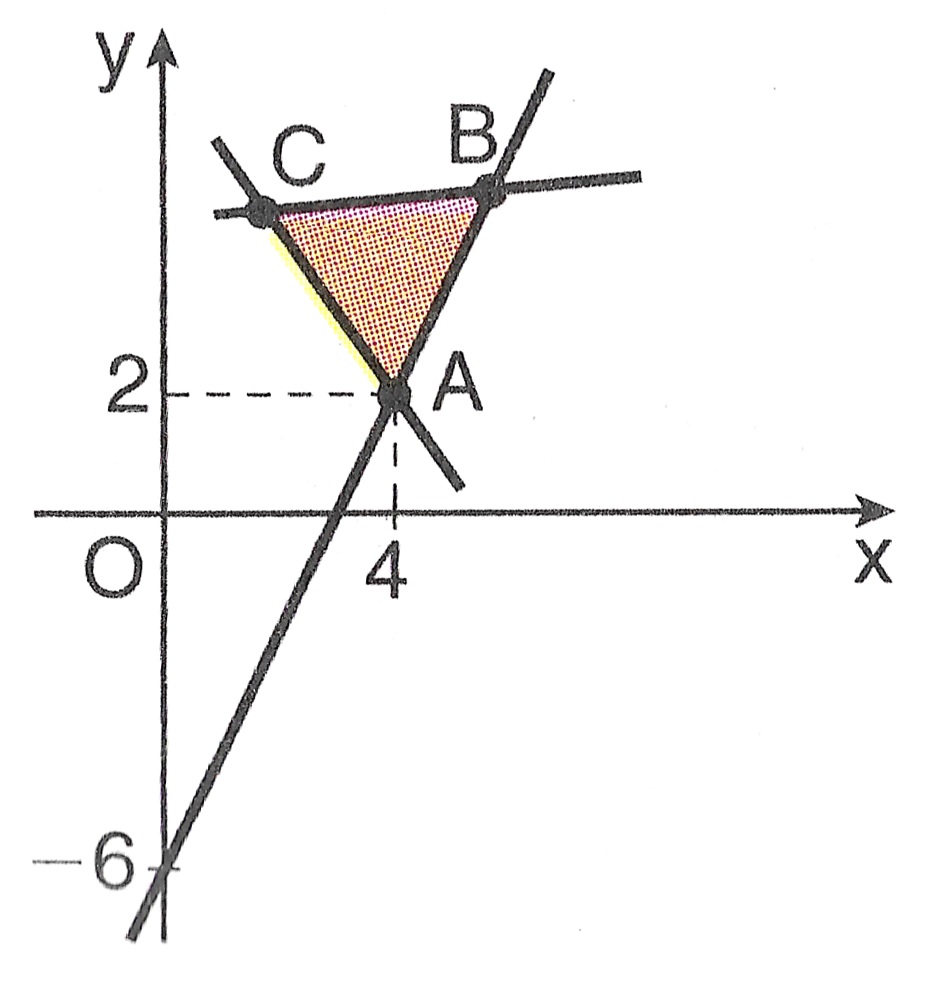
SOLUÇÃO: 

A reta que passa pelos ponto A(4,2) e D(0,-6) é dada por $$ \left| \begin{array}{ccc} 4 & 2 & 1 \\ 0 & -6 & 1 \\ x & y & 1 \end{array} \right| = 0 \Rightarrow 2x-y-6 = 0.$$ Logo, o coeficiente ângular desta reta, que é a mesma que passa por AB é dado por m_{AB} = 2 . Como o triângulo ABC é equilátero, o ângulo entre os segmentos AB e AC mede 60º. Para determinar m_{AC} = m <0, fazemos $$ \text{tg}(60º) = \left| \frac{m-2}{1 + 2m} \right| = \sqrt{3}$$ Daí $$ \frac{m-2}{1 + 2m}  = \sqrt{3} \qquad \text{ou} \qquad \frac{m-2}{1 + 2m}  = – \sqrt{3} $$ $$ m-2 = \sqrt{3} +2\sqrt{3} m \qquad \text{ou} \qquad m-2 = \sqrt{3} -2\sqrt{3} m $$ $$ m = \frac{-5 \sqrt{3} – 8 }{11} \qquad \text{ou} \qquad m = \frac{5 \sqrt{3} – 8 }{11} > 0 \text{(não convém)} .$$ Assim, $$m_{AC} = \frac{-5 \sqrt{3} – 8 }{11} $$ e AC passa por (4,2) . Vem $$y-2 = \frac{-5 \sqrt{3} – 8 }{11}  (x-4) \Rightarrow (8+ 5 \sqrt{3} )x + 11y – (54+20 \sqrt{3})=0.$$

8) O hexágono ABCDEF da figura abaixo é regular e de lado medindo 4. Encontre a equação da reta que contém o lado \overline{AB} .

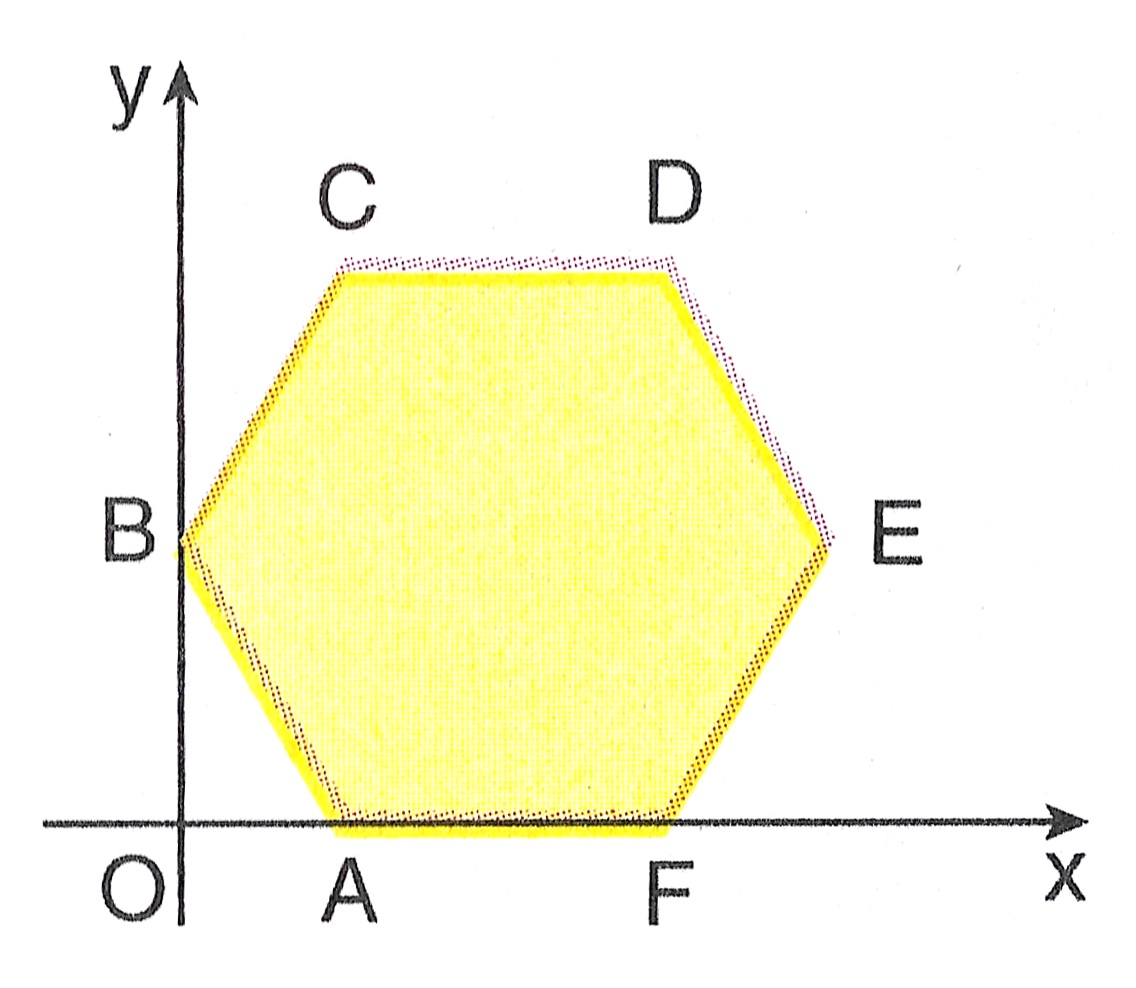
SOLUÇÃO: 

O prolongamento de \overline{BC} encontra o eixo das abscissas no ponto A' , simétrico de A em relação à origem. O triângulo AA' B , equilátero de lado 4, tem altura \overline{OB} medindo \dfrac{4 \sqrt{3}}{2} =  2 \sqrt{3}. Assim, B (0, 2 \sqrt{3} ) . Como AA' = 4 temos A(2,0). Portanto, a reta que passa por \overline{AB} tem equação dada por $$ \left| \begin{array}{ccc} 2 & 0 & 1 \\ 0 & 2 \sqrt{3} & 1 \\ x & y & 1 \end{array} \right| = 0 \Rightarrow y = -x \sqrt{3}+ 2 \sqrt{3}.$$

Leia Mais Artigos sobre Retas no Plano

• Retas No Plano Cartesiano: Posições Relativas Entre Retas
• Retas no Plano Cartesiano: Equações Reduzida, Geral, Vetorial e Paramétrica