Retas No Plano Cartesiano: Posições Relativas Entre Retas

Este artigo traz um guia claro e conciso, mas completo, da posição relativa de retas no plano cartesiano, incluindo distâncias e interseção de retas. Ideal para estudantes de graduação em disciplinas que envolvam geometria analítica no plano.

Compreender a posição relativa entre retas no plano cartesiano é um conceito importante em matemática. Este guia fornecerá uma explicação clara e concisa dos diferentes tipos de relações que podem existir entre duas retas em um plano, incluindo retas paralelas (e a distância entre elas), concorrentes (e o seu ponto de interseção) e perpendiculares (além da fórmula de calcular ângulos entre retas). Seja você um estudante ou simplesmente alguém procurando melhorar suas habilidades matemáticas, este guia é um recurso valioso.

A Geometria Analítica trabalha com a ideia de relacionar fatos geomtétricos com dados algébricos, de modo a tirar conclusões de um lado a partir de informações do outro. Neste artigo queremos estabelecer formas analíticas para determinar retas paralelas, concorrentes e coincidentes, bem como pontos de interseção entre retas.

Basicamente, duas retas no plano obrigatoriamente devem ser paralelas ou concorrentes. Até por isso, ao definirmos uma reta paralela estaremos definindo automaticamente as retas concorrentes. Desta forma, a distância entre duas retas só faz sentido ser calculada no plano se as retas são paralelas, pois, caso contrário, sendo concorrentes, sua distância é zero, afinal elas possuem um ponto de interseção.

Vamos estudar, rápida e objetivamente, a posição relativa entre retas no plano.

Retas Paralelas

Duas retas no plano serão paralelas se, e somente se, tiverem a mesma inclinação e cortarem o eixo verticam em pontos diferentes. Se cortarem o eixo vertical no mesmo ponto as retas fatalmente serão coincidentes, ou seja serão a mesma reta.

Condição de Paralelismo usando a Equação Geral da Reta

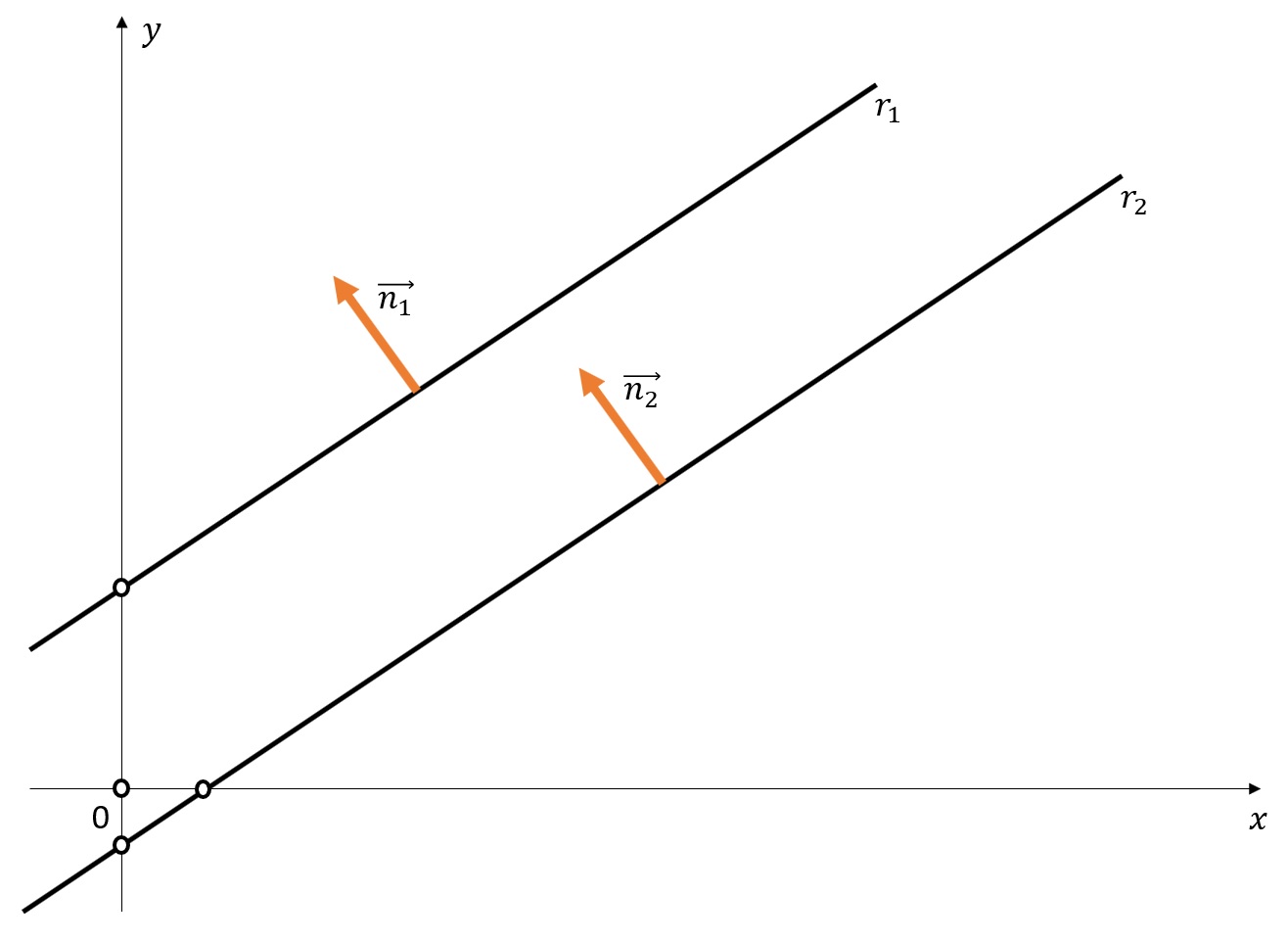
A equação geral da reta no plano é dada por $$ ax + by = c$$ onde o vetor dado por \vec{n} = (a, b) é o vetor normal à reta. Logo, duas retas $$ r_1 : a_1 x + b_1 y = c_1 \qquad \text{e} \qquad r_2 : a_2 x + b_2 y = c_2 $$ serão paralelas se os respectivos vetores normais $$ \vec{v_1} = \left( a_1 , b_1 \right) \qquad \text{e} \qquad \vec{v_2} = \left( a_2 , b_2\right) $$ são paralelos, ou seja, se existe \lambda \neq 0 \in \mathbb{R} tal que $$ \vec{v_1} = \lambda \vec{v_2} $$ ou seja, se $$ \lambda = \frac{a_1}{a_2} = \frac{b_1}{b_2}.$$

Condição de Paralelismo usando a Equação Reduzida da Reta

Duas retas paralelas formam com o eixo das abscissas ângulos congruentes: assim, se ambas possuem coeficientes angulares, estes são iguais. Observando a figura abaixo, podemos observar que uma condição de paralelismo dada por $$ m_1 = m_2$$ se $$ r_1 :  y = m_1 x +n_1  \qquad \text{e} \qquad r_2 : y = m_2 x + n_2 .$$ Se as duas retas cortam o eixo vertical em pontos diferentes elas serão paralelas e distintas, porém, se elas possuem um ponto em comum, então elas serão paralelas e coincidentes (ou seja, serão a mesma reta).

EXEMPLO 1: Para determinar a posição relativa entre as retas de equações $$r: 3x+1 \qquad \text{e} \qquad s: 9x-3y-8 = 0,$$ basta isolarmos y na equação de s : y = 3x - \dfrac{8}{3} . Assim, $$ m_r = m_s = 3.$$ Como n_r = 1 e n_s = - \dfrac{8}{3} , temos n_r \neq n_s , o que significa que r e s são paralelas distintas

EXEMPLO 2: As retas $$r: 2x-3y + 7 = 0 \qquad \text{e} \qquad s:4x – 6y + 14 = 0 $$ são coincidentes, pois além de $$ \vec{n_r} = (2, -3) = \frac{1}{2} (4 , -6) = \frac{1}{2} \vec{n_s}$$, ou seja, os vetores normais às retas serem paralelos, temos que a equação de r é múltipla à equação de s .

Condição de Paralelismo usando as Equações Vetorial e Paramétricas da Reta

Seja r uma reta que passa pelo ponto A(x_0 , y_0 ) e tema direção do vetor não nulo \vec{v} = ( \alpha , \beta ) . Sabemos que a equação vetorial da reta r é dada por $$ (x,y) = (x_0 , y_0 ) + t ( \alpha , \beta ) , \qquad t \in \mathbb{R} .$$ Daí, temos que $$ (x,y) = (x_0 + t \alpha , y_0 + t \beta) $$ donde obtemos $$ \left\{ \begin{array}{rrr} x  & = & x_0 + t \alpha \\ & \\ y &= & y_0 + t \beta \\ \end{array} \right. ; \qquad t \in \mathbb{R} .$$ Estas equações são denominadas Equações Paramétricas da reta r . O vetor \vec{v} = ( \alpha , \beta ) é chamado de vetor diretor da reta y   e t \in \mathbb{R} é chamado de parâmetro.

Duas retas em suas equações vetoriais $$ r_1: (x,y) = (x_1 , y_1 ) + t ( \alpha _1 , \beta _1 ) , \qquad t \in \mathbb{R} $$ e $$ r_2: (x,y) = (x_2 , y_2 ) + t ( \alpha _2 , \beta _2 ) , \qquad t \in \mathbb{R} $$ ou em suas equações paramétricas $$ r_1 :\left\{ \begin{array}{rrr} x  & = & x_1 + t \alpha _1 \\ & \\ y &= & y_1 + t \beta _1 \\ \end{array} \right. ; \qquad r_2 :\left\{ \begin{array}{rrr} x  & = & x_2 + t \alpha _2 \\ & \\ y &= & y_2 + t \beta _2 \\ \end{array} \right. ; \qquad t \in \mathbb{R} $$ são paralelas se seus vetores diretores são paralelos, ou seja, se existe \lambda \neq 0 \in \mathbb{R} tal que $$ \vec{v_1} = \lambda \vec{v_2} $$ ou seja, se $$ \lambda = \frac{\alpha _1}{\alpha _2} = \frac{\beta _1}{\beta _2}.$$

Retas Concorrentes

Duas retas no plano serão concorrentes se não são paralelas. Duas retas concorrentes possuem um ponto de interseção e um ângulo determinado entre elas.

Retas Perpendiculares

Um caso particular de retas concorrentes, r_1 e r_2 são as retas perpendiculares. Duas retas no plano são perpendiculares se :

1.  Os vetores normais ( \vec{n_1} e \vec{n_2} , respectivamente) ou os vetores diretores ( \vec{v_1} e \vec{v_2} , respectivamente) são normais;
2. Se o produto dos coeficientes angulares de suas retas oblíquas é igual a -1 Ou seja, se m_1 e m_2 , respectivamente, satisfazem a condição $$ m_1 \times m_2 = -1 .$$ Observe que neste caso as retas precisam ser oblíquas, pois não se define coeficiente angular para as retas verticais, porém, se uma reta é vertical – mesmo que não possamos aplicar a condição -, qualquer perpendicular a ela é, obrigatoriamente horizontal, e vice-versa.

Estes casos estão ilustrados na figura abaixo:

O Ângulo Entre duas Retas

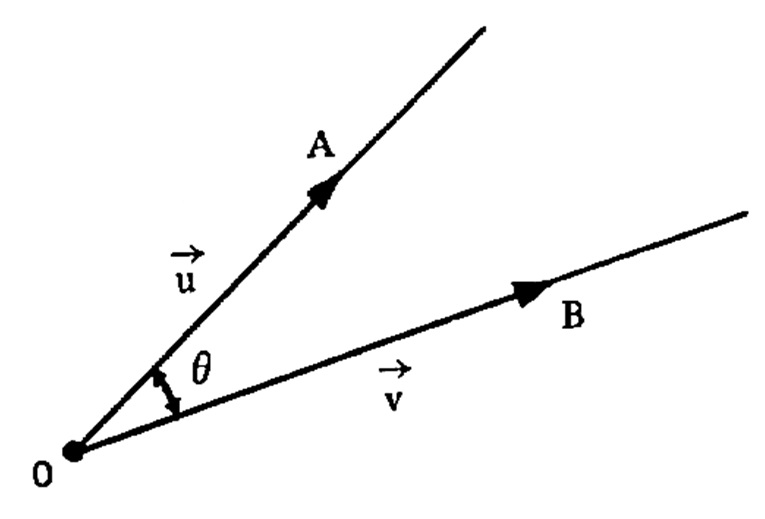
O ângulo   \theta \in [0 , \pi /2 ]  entre duas retas é determinado pelo ângulo entre os vetores normais ou entre os vetores diretores das duas retas. Lembrando que o ângulo de dois vetores   \vec{u} e   \vec{v} não nulos é o ângulo \theta formado pelas semi-retas OA e OB , tal que 0 \leq \theta \leq \pi , como na figura abaixo:

Duas retas concorrentes oblíquas dadas pelas equações reduzidas $$ r_1 :  y = m_1 x +n_1  \qquad \text{e} \qquad r_2 : y = m_2 x + n_2 .$$ tem seu ângulo   \theta \in [0 , \pi /2 ] definido pela relação $$ \text{tg} ( \theta ) = \left| \frac{m_2 – m_1}{1 + m_2 m_1} \right|.$$

A Interseção de retas.

O ponto P \left(x_p , y_p \right)   de interseção de duas retas r e s , concorrentes, pertence evidentemente a cada uma das retas e assim, por isso, mesmo, suas corrdenadas devem satisfazer as equações de ambas as retas, ao mesmo tempo.

Considerando as retas $$ r: a_1 x + b_1 y + c_1 =0 \qquad \text{e} \qquad s: a_2 x + b_2 y +  c_2 = 0 $$ dadas na forma geral, este ponto P \left(x_0 , y_0 \right) será a solução do sistema linear $$ \left\{ \begin{array}{lll} a_1 x + b_1 y + c_1 & = & 0 \\ & & \\ a_2 x + b_2 y +  c_2 = 0  \end{array}\right. $$ que consiste no sistema de duas equações lineares a duas incógnitas.

Note que se as equações das retas são dadas na forma reduzisa, poderá ser utilizado o mesmo processo. Os casos para as demais formas de escrever as equações das retas r e s são melhor trabalhados convertendo-as nas equações gerais.

A Distância entre Ponto e Reta e a Distância entre Retas

Por fim, cabe nos dar uma fórmula para a distância entre duas retas paralelas.

Sem perda de generalidade podemos tomar as equações gerais como $$ r: ax + by + c_1 =0 \qquad \text{e} \qquad s: ax + by +  c_2 = 0 $$, pois elas podem ser definidas pelo mesmo vetor normal, mas passam por pontos diferentes. Obviamente sduas retas que passam pelo mesmo ponto e com o mesmo vetor normal são concorrentes. O problema consiste em dado um ponto P na reta s , encontrar a distância entre P e o pé da perpendicular a r , que será o ponto Q na reta r baixada por P . Neste caso, $$ d(P,r) = d(P,Q),$$ ou seja, a distância de P até r será a distância de P até este ponto Q , conforme podemos ver na figura abaixo:

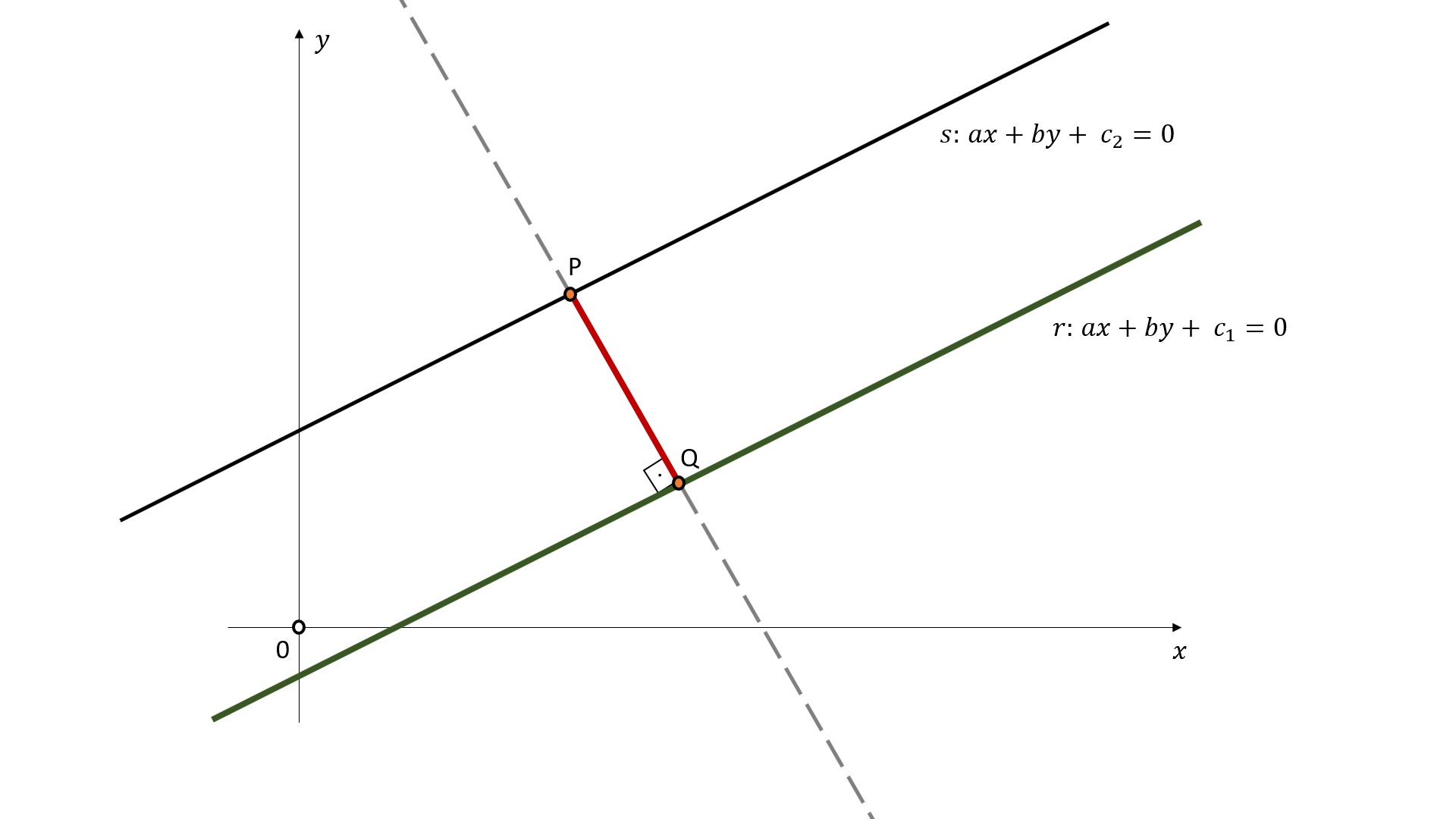
Torna-se fácil, tendo a equação de r , encontrar a equação de sua reta perpendicular p , passando pelo P fora de r . Interceptando r e p , obtemos o ponto Q ; basta encontrarmos a distância entre P e Q que o problema se resolve.

Adotando r: ax + by = c_1 e P \left(x_0 , y_0 \right) como a reta e o ponto em questão e seguísseo o caminho descrito acima, chegaríamos a $$ d(r, P) = \frac{| a x_0 + b y_0 + c_1 |}{\sqrt{a^2 + b^2}}.$$ Observe que como tomamos a equação geral da reta r , logo seu vetor normal é dado por \vec{n} = (a,b) , o que nos permite escrever $$ d(r, P) = \frac{| a x_0 + b y_0 + c_1 |}{| \vec{n}|}.$$

Agora, para encontrar a distância entre as retas $$ r: ax + by + c_1 = 0 \qquad \text{e} \qquad s: ax + by + c_2 = 0 $$ basta considerar que P é um ponto de s e usar a mesma fórmula. Ou seja, P \left(x_0 , \dfrac{c_2 - ax_0}{b}\right) , portanto $$ d(r, s) = \frac{ \left| a x_0 + b \frac{c_2 – ax_0}{b} + c_1 \right|}{\sqrt{a^2 + b^2}}= \frac{| a x_0 +c_2 – ax_0  + c_1 |}{\sqrt{a^2 + b^2}} = \frac{| c_2   + c_1 |}{\sqrt{a^2 + b^2}}$$

Leia Mais Sobre Geometria Analítica no Plano:

• Retas no Plano Cartesiano: Equações Reduzida, Geral, Vetorial e Paramétrica
• Vetores no Plano R²: Norma e Produto Escalar
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• O Espaço R²: Coordenadas no Plano Cartesiano