Matrizes e Determinantes: 7 Exercícios Resolvidos passo-a-passo

Procurando exercícios resolvidos sobre matrizes e determinantes? Confira estes 7 exercícios resolvidos detalhadamente que irão te ajudar a melhorar sua compreensão e habilidades de resolução de problemas neste tópico.

Se você está estudando matrizes e determinantes e precisa de ajuda, compilamos uma lista de 7 exercícios resolvidos que o ajudarão a melhorar sua compreensão e habilidades de resolução de problemas neste tópico. Quer você seja um estudante nos primeiros anos da graduação ou apenas queira aprimorar suas habilidades matemáticas, esses exercícios certamente serão benéficos.

O que é uma Matriz?

Uma matriz é uma  dupla sequência de números, símbolos ou expressões organizadas em linhas e colunas. É comumente usada em matemática para representar e manipular dados ou resolver sistemas de equações lineares.

Cada elemento de uma matriz é identificado pela sua posição, com o número da linha indicando a posição horizontal e o número da coluna indicando a posição vertical. As matrizes podem ser adicionadas, subtraídas, multiplicadas e transformadas por meio de diversas operações, o que as torna um conceito fundamental em álgebra linear.

Leia Mais: Matrizes – Definições Básicas e Primeiros Exemplos

O que é o Determinante de uma Matriz?

Na álgebra linear, o determinante de uma matriz é um valor escalar que pode ser calculado a partir dos elementos da matriz. É denotado por det(A) ou |A|, onde A representa a matriz. O determinante fornece informações importantes sobre a matriz, como se ela é invertível ou singular.

O determinante é usado em diversas aplicações, incluindo resolução de sistemas de equações lineares, localização da área ou volume de formas geométricas e determinação dos autovalores e autovetores de uma matriz. O determinante pode ser calculado usando diferentes métodos dependendo de sua ordem, como a Regra de Sarrus e o Teorema de Laplace, por exemplo.

Leia Mais: Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió

Por que é tão importante estudar Matrizes e Determinantes?

Estudar matrizes e determinantes é importante porque são conceitos fundamentais em álgebra linear e têm inúmeras aplicações em diversos campos, como matemática, engenharia, ciência da computação e física.

Matrizes são usadas para representar e resolver sistemas de equações lineares, transformar formas geométricas, analisar redes e realizar operações em computação gráfica e análise de dados. Os determinantes, por outro lado, são usados para determinar se uma matriz é invertível, calcular áreas e volumes, resolver sistemas de equações e encontrar autovalores e autovetores.

A compreensão de matrizes e determinantes permite uma compreensão mais profunda dessas aplicações e aprimora as habilidades de resolução de problemas nessas áreas.

Saiba Mais: Assista nosso curso gratuito sobre Matrizes e Determinantes

Os 5 Melhores Livros Para estudar Matrizes e Determinantes

1. “Fundamentos de matemática elementar – Volume 4: Sequências, matrizes, determiantes e sistema”, de Gelson Iezzi.
2. “Matrizes e Determinantes. Teoria e Exercícios Resolvidos”, de Rogério Bastos Pimentel Pereira.
3. “Álgebra Linear”, de Alfredo Steinbruch
4. “Matrix Operations” (Coleção Shaum), de Richard Bronson
5. “Álgebra Linear”, de J. L. Boldrini e outros

7 Exercícios Resolvidos Sobre Matrizes e Determinantes

1) Calcule o determinante da matriz $$A = \left[ \begin{array}{rrrr} 8 & 0 & -4 & 1\\ 2 & 3 & 2 & 2 \\ 1 & -3 & 5 & 7\\ -4 & 0 & 2 & 5\\ \end{array} \right].$$

Solução: A segunda coluna já contém dois zeros. Um terceiro zero pode ser obtido nesta coluna (aplicando o Teorema de Jacobi) adicionando-se a terceira linha à segunda linha. Então temos $$ \left[ \begin{array}{rrrr} 8 & 0 & -4 & 1\\ 2 & 3 & 2 & 2 \\ 1 & -3 & 5 & 7\\ -4 & 0 & 2 & 5\\ \end{array} \right] \sim \left[ \begin{array}{rrrr} 8 & 0 & -4 & 1\\ 3 & 0 & 7 & 9 \\ 1 & -3 & 5 & 7\\ -4 & 0 & 2 & 5\\ \end{array} \right].$$ Agora, aplicando o Teorema de Laplace para determinantes, encontramos $$ \text{det}(A) = (-1)^{3+2} \times (-3) \times \left| \begin{array}{rrrr} 8 & -4 & 1\\ 3 & 7 & 9 \\  -4 & 2 & 5\\ \end{array} \right| .$$ Agora, usando a Regra de Sarrus, encontramos $$ \text{det}(A) =3 \times \left[ 280 + 144 + 6 +28 – 144 +60\right] = 3 \times 374 = 1.122$$

2) Considere as matrizes $$ A = \left[ \begin{array}{rrr} 1 & -2 & 1\\ 0 & 2 & -1 \\ 2 & 1 & 1\\ \end{array} \right] \qquad e \qquad B = \left[ \begin{array}{rrr} 2 & 1 & -1\\ 1 & -1 & 0 \\ 2 & -1 & 1\\ \end{array} \right] .$$ Verifique se as matrizes comutam.

Solução: Da definição de multiplicação de matrizes, sabemos que estas duas matrizes comutam se, e somente se, A \times B = B \times A . Assim, temos que Analogamente, vemos que

Portanto, claramente temos que A \times B \neq B \times A .

3) Encontre, se possível, a inversa da matriz $$ A = \left[ \begin{array}{rrr} 1 & -1 & -1\\ 3 & -1 & 2 \\ 2 & 2 & 3\\ \end{array} \right] $$ usando o escalonamento.

Solução: Usaremos o Método de Gauss-Jordan (ou escalonamento):

1) Primeiramente vamos multiplicar a primeira linha por (-3) e soma-la na segundo linha. Em seguida multiplicamos a primeira linha por (-2) e a somamos à terceira linha. Com isso, obtemos

2) Agora iremos multiplicar a segunda linha por 1/2 :

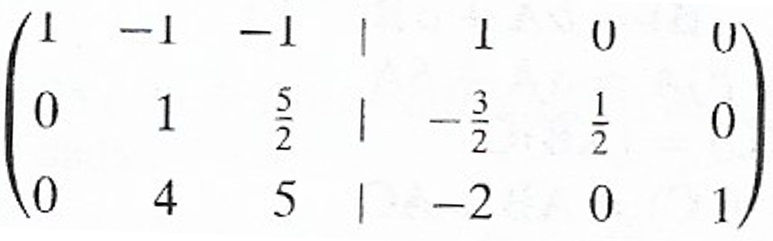
3) Vamos, agora, somar a segunda linha à primeira e, em seguida, multiplicamos a segunda linha por (-4) e somamos na terceira linha:

4) Multilicamos 1/5 à terceira linha para encontrar a diagonal principal da matriz identidade e zeros em todas as entradas abaixo dela:

5) Por fim, multiplique a terceira linha por - 3/2 e some na primeira linha. Em seguida multiplique a terceira linha por -5/2 e some à segunda linha. Assim, obteremos a matriz identidade à esquerda e a matriz inversa à direita:

Portanto, $$ A^{-1} = \left[ \begin{array}{rrr} \frac{7}{10} & -\frac{1}{10} & \frac{3}{10}\\ \frac{1}{2} & – \frac{1}{2} & \frac{1}{2} \\ -\frac{4}{5} & \frac{2}{5}  & – \frac{1}{5} \\ \end{array} \right] $$

4) Considere a matriz $$ \left[ \begin{array}{rrr} 0 & 1 & 1\\ 1 & 0 & 1 \\ 1 & 1 & 0\\ \end{array} \right] .$$

a) Sendo I_{3} a matriz identidade e t \in \mathbb{R} um número real qualquer. Determine a matriz $$B= A – t \times I_{3} .$$

Solução: Facilmente percebemos que $$ B = A – t \times I_{3} = \left[ \begin{array}{rrr} 0 & 1 & 1\\ 1 & 0 & 1 \\ 1 & 1 & 0\\ \end{array} \right] – t \times  \left[ \begin{array}{rrr} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{array} \right] = \\ \left[ \begin{array}{rrr} 0 & 1 & 1\\ 1 & 0 & 1 \\ 1 & 1 & 0\\ \end{array} \right] – \left[ \begin{array}{rrr} t & 0 & 0\\ 0 & t & 0 \\ 0 & 0 & t \\ \end{array} \right] = \\ \left[ \begin{array}{rrr} -t & 1 & 1\\ 1 & -t & 1 \\ 1 & 1 & -t\\ \end{array} \right].$$

b) Calcule \text{det} \left( A - t \times I_{3} \right) ;

Solução: Para calcular este determinante usamos a Regra de Sarrus: $$ \text{det} \left( A – t \times I_{3} \right) = \left| \begin{array}{rrr} -t & 1 & 1\\ 1 & -t & 1 \\ 1 & 1 & -t\\ \end{array} \right| = -t^3+3t+2 = 0.$$

c) Para quais valores de t \in \mathbb{R} temos \text{det} \left( A - t \times I_{3} \right) = 0 ?

Solução: Para que \text{det} \left( A - t \times I_{3} \right) = 0 precisamos encontrar as raízes do polinômio p(t) = -t^3+3t+2 . Facilmente podemos encontrar t_1 = -1 como raíz deste polinômio e usando o dispositivo de Briot-Rufini encontramos que $$ -t^3+3t+2 = (t+1)(-t^2+t+2)$$ e, usando a fórmula de Bhaskara, encontramos que $$ -t^3+3t+2 = (t+1)(-t^2+t+2) = (t+1)(-t-1)(t-2) = -(t+1)^2 (t-2)$$ Portanto, para que \text{det} \left( A - t \times I_{3} \right) = 0 , basta que t =-1 ou t = 2 .

5) Considere o conjunto das matrizes na forma $$ \left[ \begin{array}{rr} x-3 & x+k \\ 1 & x-5 \\ \end{array} \right], \qquad x \in \mathbb{R} . $$ Determine o valor de k para o qual exista exatamente uma matriz não inversível neste conjunto.

Solução: Como queremos uma matriz não-inversível, então precisamos que $$ \left| \begin{array}{rr} x-3 & x+k \\ 1 & x-5 \\ \end{array} \right| = 0 $$ ou seja, precisamos que $$ (x-3)(x-5) – 1 (x-k) = x^2 -8x+15-x-k = x^2-9x+15 -k = 0 $$ O discriminante desta equação do segundo grau é dado por $$ \Delta = 81 – 4(15 – k).$$ Para esta equação do segundo grau, teremos que

1. As matrizes nesta forma terão duas matrizes não-inversíveis se \Delta > 0 ;

2. As matrizes nesta forma terão exatamente uma matriz não inversível se \Delta = 0 ;

3. As matrizes nesta forma sempre serão inversíveis se \Delta <0 ;

Desta forma, para que esta equação do segundo grau tenha solução real, precisamos que \Delta \geq 0 . Observe que $$ 81 – 4(15 – k) \geq 0 \Leftrightarrow 81 \geq 4(15 – k) \Leftrightarrow \frac{81}{4} – 15 \geq -k \Leftrightarrow k \geq – \frac{21}{4}.$$ Logo, temos três conclusões:

1. As matrizes nesta forma terão duas matrizes não-inversíveis se k > - \dfrac{21}{4} ;

2. As matrizes nesta forma terão exatamente uma matriz não inversível se k = - \dfrac{21}{4} ;

3. As matrizes nesta forma sempre serão inversíveis se k < - \dfrac{21}{4} ;

Portanto,   k = - \dfrac{21}{4} é o valor para o qual existe exatamente uma matriz não inversível neste conjunto.

6) Sejam A e B duas matrizes quadradas de mesma ordem. Neste caso, sabemos que \text{det}(A \cdot B) = \text{det}(A) \cdot \text{det}(B)  . Mostre que, se n \in \mathbb{N}^{*} , temos $$ \text{det} \left( A^{n} \right) = \left[ \text{det}(A) \right]^{n}.$$

Solução: Observe que para n = 2 e n = 3 a propriedade, de fato se justifica: $$ \text{det} \left( A^{2} \right) = \text{det} \left( A \cdot A \right) = \text{det}(A) \cdot \text{det}(A) = \left[ \text{det}(A) \right]^2. $$ $$ \text{det} \left( A^{3} \right) = \text{det} \left( A^{2} \cdot A \right) = \left[ \text{det}(A) \right]^2 \cdot \text{det}(A)  = \left[ \text{det}(A) \right]^3. $$ Assim, assumindo que a propriedade é válida para n \in \mathbb{N}^{*} , ou seja, que $$ \text{det} \left( A^{n} \right) = \left[ \text{det}(A) \right]^{n},$$ temos que, para n +1 a afirmação também é válida: $$ \text{det} \left( A^{n+1} \right) = \text{det} \left( A^{n} \cdot A \right) = \left[ \text{det}(A) \right]^{n} \cdot \text{det}(A) = \left[ \text{det}(A) \right]^{n+1}. $$ Portanto, por esta técnica de indução finita podemos garantir que \text{det} \left( A^{n} \right) = \left[ \text{det}(A) \right]^{n} .

7) Sendo A uma matriz inversível, mostre que $$ \text{det} \left( A^{-1} \right) =  \frac{1}{\text{det}(A)} .$$

Solução: Seja A uma matriz inversível, então $$ A \cdot A^{-1} = I .$$ Assim, sabendo que \text{det}(A \cdot B) = \text{det}(A) \cdot \text{det}(B)  , então temos que $$ \text{det} \left( A \cdot A^{-1} \right) = \text{det}(I) \Rightarrow \text{det}(A) \cdot \text{det}\left( A^{-1} \right)  = \text{det}(I) \Rightarrow \\  \Rightarrow \text{det}(A) \cdot \text{det}\left( A^{-1} \right)  = 1 \Rightarrow \text{det} \left( A^{-1} \right) =  \frac{1}{\text{det}(A)}.$$

Os 5 Melhores Livros Para estudar Matrizes e Determinantes

1. “Fundamentos de matemática elementar – Volume 4: Sequências, matrizes, determiantes e sistema”, de Gelson Iezzi.
2. “Matrizes e Determinantes. Teoria e Exercícios Resolvidos”, de Rogério Bastos Pimentel Pereira.
3. “Álgebra Linear”, de Alfredo Steinbruch
4. “Matrix Operations” (Coleção Shaum), de Richard Bronson
5. “Álgebra Linear”, de J. L. Boldrini e outros