Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió

Quer calcular o determinante de uma matriz quadrada? Este guia irá ajudá-lo através do processo passo a passo, com exemplos, pelos métodos de Sarrus, Laplace, Vandermonde e Chió.

Ao estudarem a teoria dos sistemas lineares durante o século XVII, os matemáticos Leibniz (1646 – 1716), na Alemanha, e Kowa (1642 – 1708), no Japão, sentiram a necessidade de criar certas expressões matemáticas, definidas a partir dos coeficientes das incógnitas dos sistemas. Essas expressões estão relacionadas a matrizes e foram denominadas determinantes, nome que foi utilizado no século XVIII pelo matemático Gauss.

O que é o determinante de uma matriz?

Uma matriz A, m \times n (lê-se: m por n), é uma tabela de m \cdot n números dispostos em m linhas e n colunas. Desta forma, representamos uma matriz colocando a tabela dentro de parênteses ou de colchetes, ou ladeado a tabela, à esquerda e à direita, por duas barras verticais, do seguinte modo: $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right] .$$

O determinante associa a cada matriz quadrada A um único número real que denominamos determinante de A. Indicamos este número real por \text{det} (A) ou colocamos o elementos da matriz A entre duas barras verticais.

As 10 Propriedades Gerais do Determinante

1. \text{det} (A)= \text{det} (A^t), ou seja, o determinante de uma matriz é igual ao determinante de sua transposta;
2. Se B é a matriz que se obtém de uma matriz quadrada A, quando trocamos entre si a posição de duas fileiras paralelas, então \text{det} (A) = - \text{det} (B) ;
3. Uma matriz A que possui duas filas paralelas “iguais” tem determinante igual a zero;
4. O determinante de uma matriz com uma linha ou coluna multiplicada por uma constante real é igual ao determinante desta matriz multiplicada pela mesma constante;
5. Uma consequência da propriedade anterior é: \text{det} (k.A)= k^n . \text{det} (A), sendo k uma constante real e n a ordem da matriz;
6. Ao calcularmos um determinante, podemos “colocar em evidência” um “fator comum” de uma fila (seja ela linha ou coluna);
7. [Teorema de Jacobi] O determinante não se altera quando adicionamos uma fila qualquer com outra fila paralela multiplicada por um número;
8. Quando uma fila de um determinante é igual à soma de múltiplos de filas paralelas , o determinante é igual a zero.
9. [Teorema de Binet] Sendo A e B matrizes quadradas de mesma ordem, então \text{det} (A.B)=\text{det} (A).\text{det} (B);
10. Sendo A uma matriz triangular, o seu determinante é o produto dos elementos da diagonal principal.

Determinante de uma matriz de ordem 2

Seja a matriz quadrada de ordem dois A = \left[ \begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{array} \right]. Denominamos de determinante dessa matriz o número $$\text{det} (A)=\left| \begin{array} {cc} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{array} \right| = a_{11}a_{22} – a_{21}a_{12}.$$

Ou seja, o determinante de uma matriz quadrada de ordem 2 é o produto dos elementos da diagonal principal menos o produto dos elementos da diagonal secundária.

EXEMPLO: Considere a matriz A = \left[\begin{array}{cc} 1 & 2\\ 2 & 3\\ \end{array} \right]. O determinante dessa matriz o número $$\text{det} (A)=\left| \begin{array}{cc} 1 & 2\\ 2 & 3\\ \end{array} \right| = 1.3 – 2.2 = 3 – 4 = -1.$$

EXEMPLO: Resolva em \mathbb{R}: $$\left| \begin{array}{cc} x & 2\\ 1 & -3\\ \end{array} \right| < 4.$$ Calculado o determinante do primeiro termo, vem $$ -3x-2 < 4 \Rightarrow -3x < 6 \Rightarrow x > -2.$$ Portanto, o conjunto solução deste problema é dado por $$ S = \left\{ x \in \mathbb{R} | x > -2 \right\}.$$

Determinante de uma matriz de ordem 3: A Regra de Sarrus

Seja a matriz quadrada de ordem 3: $$A = \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right].$$ O determinante desta matriz é dado por $$\text{det} (A)=\left| \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right| = \\ = a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{21} a_{32} a_{13} – a_{13} a_{22} a_{31} – a_{12} a_{21} a_{33} – a_{23} a_{32} a_{11}.$$

Como usar a Regra de Sarrus para calcular determinantes?

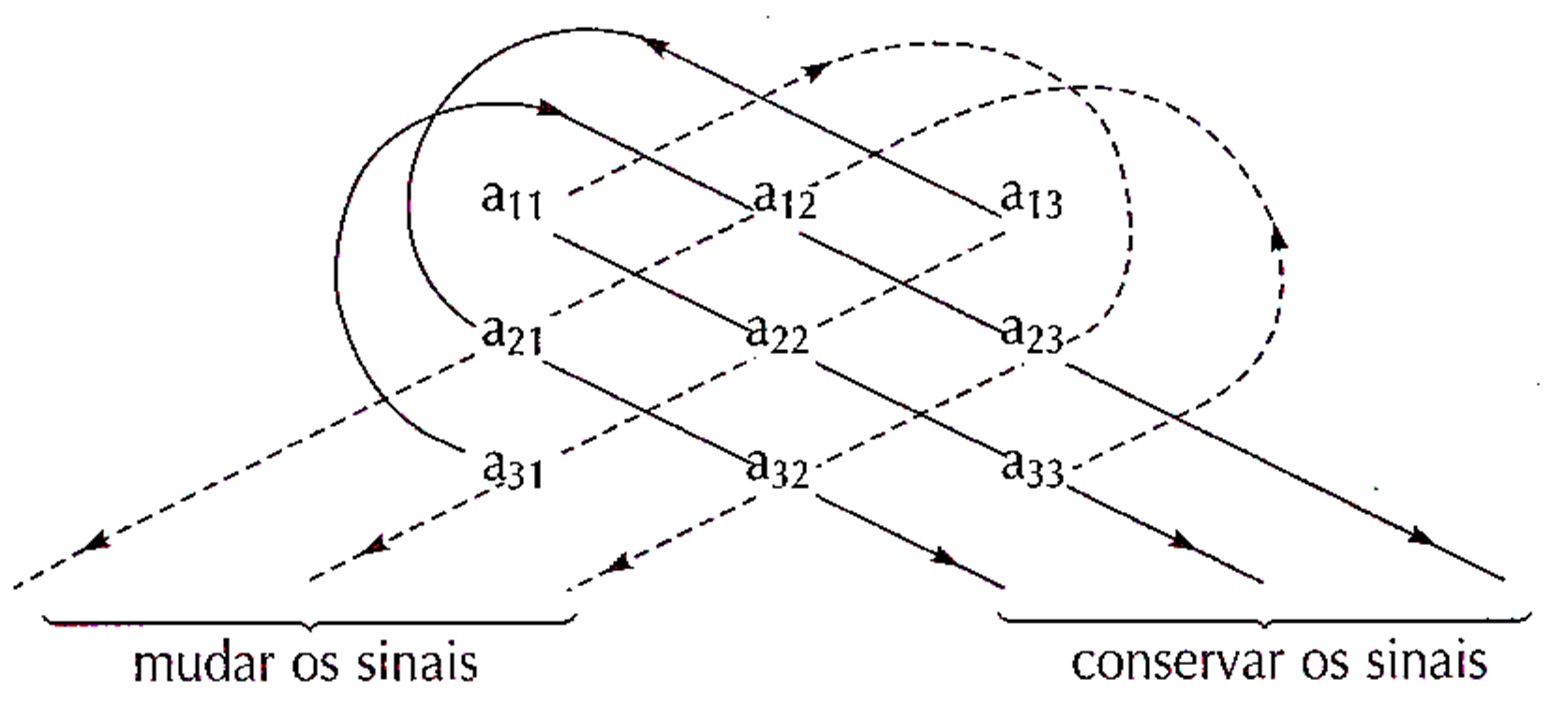
Para calcularmos o determinante de uma matriz de ordem 3, usamos um dispositivo prático conhecido como Regra de Sarrus, descoberta pelo matemático francês P. F. Sarrus, em 1833.

Considerando ainda a matriz $$A = \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right],$$ para calcular o determinante desta utilizando a Regra de Sarrus:

1. À direita da matriz A repetimos as duas primeiras colunas da matriz;
2. Multiplicamos os elementos situados em cada direção paralela à diagonal principal e somamos os produtos;
3. Multiplicamos os elementos situados em cada direção paralela à diagonal secundária e do resultado anterior subtraímos esses produtos.

Este dispositivo pode ser ilustrado pelo esquema da figura abaixo:

OBSERVAÇÃO:

1. A regra de Sarrus também pode ser utilizada repetindo a primeira e segunda linhas abaixo da matriz, ao invés de repetirmos a primeira e segunda colunas, e usamos a mesma lógica para os produtos das diagonais principal e secundária.
2. Podemos, também, obter os seis termos do \text{det} (A) para matrizes de ordem 3, usando o seguinte esquema:

EXEMPLO: Vamos calcular o determinante da matriz $$A = \left[ \begin{array}{ccc} 3 & 2 & 1\\ 2 & 4 & 3\\ 1 & 5 & 2\\ \end{array} \right].$$ Seguindo o esquema da Regra de Sarrus ilustrado abaixo, encontramos

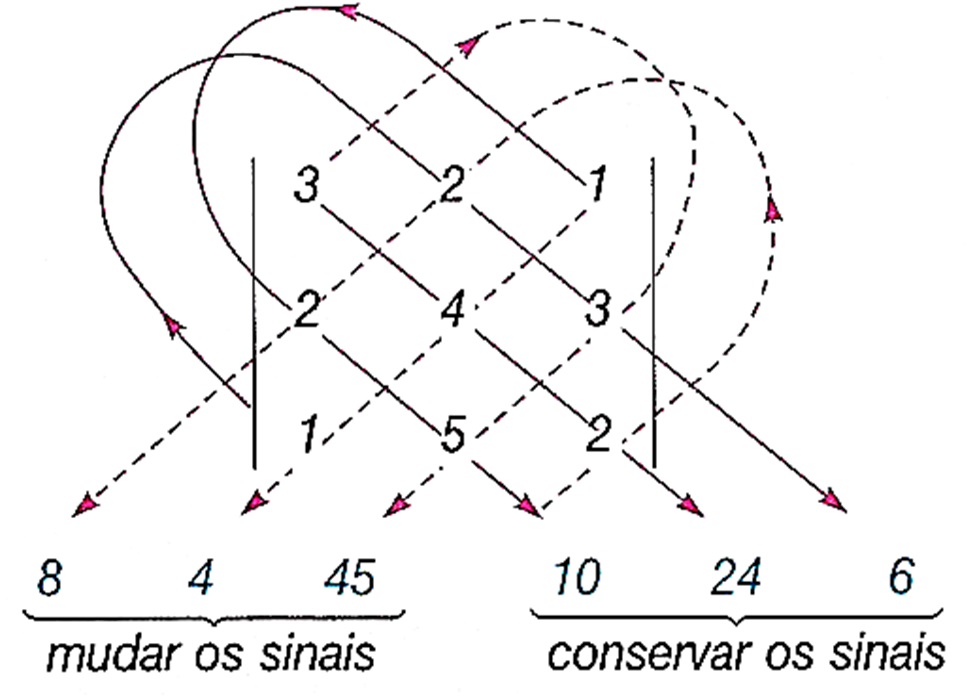
$$ \text{det} (A) = 10 + 24 +6 -8 -4 -45 = -17.$$

Determinante de Ordem Superior: O Método de Laplace

Dada uma matriz quadrada A de ordem n (n\geq 2) , denominamos menor complementar do elemento a_{ij} , e o indicamos por M_{ij}, o determinante da matriz quadrada de ordem n-1 que se obtêm suprimindo a linha i e a coluna j da matriz A . Denominamos de cofator do elemento a_{ij} e indicamos por A_{ij} , o número (-1)^{i+j}.M_{ij}.

TEOREMA DE LAPLACE: Seja A uma matriz quadrada de ordem n (n\geq 2) , seu determinante é a soma dos produtos dos elementos de uma fila (linha ou coluna)qualquer pelos respectivos cofatores.

Pelo teorema acima, dada uma matriz $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right], $$ seu determinante pode ser dado pelo somatório $$ \text{det} (A) = \sum\limits_{i = 1}^{n}{(-1)^{i+j} a_{ij} .M_{ij}} = \\ = (-1)^{1+j} a_{1j} .M_{1j}+(-1)^{2+j} a_{2j} .M_{2j} + … + (-1)^{n+j} a_{nj} .M_{nj}$$ se fixada uma coluna j , ou por $$ \text{det} (A) = \sum\limits_{j = 1}^{n}{(-1)^{i+j} a_{ij} .M_{ij}} = \\ = (-1)^{i+1} a_{i1} .M_{i1}+(-1)^{i+2} a_{i2} .M_{i2} + … + (-1)^{i+n} a_{in} .M_{in}$$ se fixada uma linha i .

EXEMPLO: Sendo A = \left[ \begin{array}{cccc} 1 & 2 & 5 & -1\\ 0 & 2 & 0 & 0 \\ -1 & 4 & 2 & 3\\ 2 & 1 & 3 & 1\\ \end{array} \right] , vamos usar o Método de Laplace para calcular \text{det} (A) . Como podemos utilizar qualquer linha ou coluna da matriz, iremos escolher a segunda linha. Assim, $$ \text{det} (A) = \sum\limits_{j = 1}^{4}{(-1)^{2+j} a_{2j} .M_{2j}} = \\ = (-1)^{2+1} a_{21} .M_{21}+(-1)^{2+2} a_{22} .M_{22} +(-1)^{2+3} a_{23} .M_{23} + (-1)^{2+4} a_{24} .M_{24} = \\ = – 0 .M_{21}+ 2 .M_{22} – 0 .M_{23} + 0 .M_{24} = 2 .M_{22} = \\ = 2 . \left| \begin{array}{ccc} 1 & 5 & -1 \\ -1 & 2 & 3 \\ 2 & 3 & 1\\ \end{array} \right| = 2 \times 35 = 70.$$

Note que a escolha feita nos leva ao cálculo de apenas 1 co-fator; se usássemos a 1ª linha da matriz, deveríamos calcular 4 co-fatores. É importante ressaltar que independente de qual seja a sua escolha o valor do determinante deverá ser o mesmo.

EXEMPLO: Sendo A = \left[ \begin{array}{cccc} 5 & 0 & 1 & 2\\ 3 & 2 & 1 & 0 \\ 4 & 1 & 0 & 0\\ 3 & -2 & 2 & 0\\ \end{array} \right] , vamos usar o Método de Laplace para calcular \text{det} (A) . Como podemos utilizar qualquer linha ou coluna da matriz, iremos escolher a quarta coluna, pois nela está o maio número de zeros e teremos que calcular apenas um co-fator. Neste caso, como a_{24} = a_{34} = a_{14} = 0 , então $$ \text{det} (A) = (-1)^{1+4} a_{14} M_{14} = – 2 \times \left| \begin{array}{ccc} 3 & 2 & 1 \\ 4 & 1 & 0 \\ 3 & -2 & 2\\ \end{array} \right|=-2\times(-21)=42.$$

OBSERVAÇÕES:

1. No cálculo do determinante de uma matriz de ordem n , recaímos em determinantes de matrizes de ordem n - 1, e no cálculo destes, recaímos em determinantes de ordem n -2 , e assim sucessivamente, até recairmos em determinantes de matrizes de ordem 3, que calcularmos com a regra de Sarrus, por exemplo;
2. O cálculo de um determinante fica mais simples quando escolhemos uma fila com a maior quantidade de zeros;
3. A aplicação sucessiva e conveniente do Teorema de Jacobi (enunciado acima com uma das propriedades do determinante), pode facilitar o cálculo do determinante pelo teorema de Laplace. O próximo exemplo ilustra esta técnica.

EXEMPLO: Vamos calcular o determinante da matriz A = \left[ \begin{array}{cccc} 1 & 2 & 3 & 1\\ 0 & -1 & 2 & 1 \\ -2 & 3 & 1 & 2 \\ 3 & 4 & 6 & 3 \\ \end{array} \right] .

Observe que a 1ª coluna ou a 2ª linha tem a maior quantidade de zeros. Nos dois casos, se aplicarmos o teorema de Laplace ainda calcularemos três cofatores. Para facilitar, vamos

1. multiplicar a 1ª linha por 2 e somar com a 3ª linha;
2. multiplicar a 1ª linha por – 3 e somar com a 4ª linha.

Fazendo isso, teremos a matriz equivalente a A dada por B = \left[ \begin{array}{cccc} 1 & 2 & 3 & 1\\ 0 & -1 & 2 & 1 \\ 0 & 7 & 7 & 4 \\ 0 & -2 & -3 & 0 \\ \end{array} \right] e pelo teorema de Jacobi temos que $$ \text{det} (A) = \text{det} (B) = (-1)^{1+1}1 \times \left| \begin{array}{ccc} -1 & 2 & 1 \\ 7 & 7 & 4 \\ -2 & -3 & 0\\ \end{array} \right| = -35.$$

O Determinante de Vandermonde

Um determinante de ordem ordem n (n\geq 2) é chamado determinante de Vandermonde ou  determinante das potências se, e somente se, na 1ª linha (ou coluna) os elementos forem todos iguais a 1; na 2ª linha números quaisquer; na 3ª, os seus quadrados; na 4ª, os seus cubos e assim sucessivamente.

Um determinante de Vandermonde é igual ao produto de todas as diferenças que se obtém subtraindo-se de cada um dos elementos característicos os elementos precedentes, independente da ordem do determinante. Os elementos da 2 linha são chamados de elementos característicos.

EXEMPLO: Vamos calcular o determinante \text{det} (V) = \left| \begin{array}{ccc} 1 & 1 & 1 & 1 \\ 2 & 3 & 4 & 5 \\ 4 & 9 & 16 & 25 \\ 8 & 27 & 64 & 125 \\  \end{array} \right| . Como este se trata de um determinante de Vandermonde, logo, seus elementos característicos são 2,3,4 e 5. As diferenças possíveis são (3-2), (4-2), (4-3), (5-2), (5-3) e (5-4). Desta forma, podemos escrever que $$ \text{det} (V) = (3-2) \times (4-2) \times (4-3) \times (5-2) \times (5-3) \times (5-4) = 12.$$

A Regra de Chió para Determinantes

Esta regra é uma aplicação direta do teorema de Jacobi; permite abaixar a ordem de um determinante para simplificar o seu cálculo. Para poder aplicar a regra de Chió no cálculo de um determinante, precisamos de uma matriz quadrada de ordem n \geq 2 , com a_{ij} = 1 .

Para usar a regra de Chió basta seguir as três etapas à seguir:

1. 1ª Etapa: eliminamos da matriz dada a linha i e a coluna j , do elemento a_{ij} = 1 ;
2. 2ª Etapa: subtraímos de cada um dos elementos restantes A o produto dos elementos eliminados que se encontram na sua linha e na sua coluna, obtendo assim uma matriz  B de ordem n - 1 .
3. 3ª Etapa: o determinante de A é igual a (-1)^{i+j} \times \text{det} (B) .

EXEMPLO: Vamos calcular o determinate da matriz $$ A = \left[ \begin{array}{cccc} 2 & 3 & -1 & 0 \\ 1 & 4 & 2 & 1 \\ 3 & 2 & 2 & 0 \\ -1 & 2 & 3 & 2 \\ \end{array} \right] $$ usando a regra de Chió à partir do elemento a_{24} = 1 :

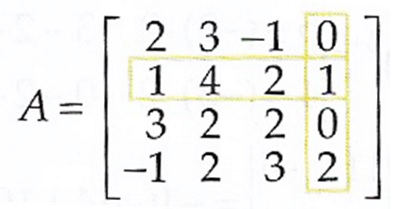
A partir daqui teremos:

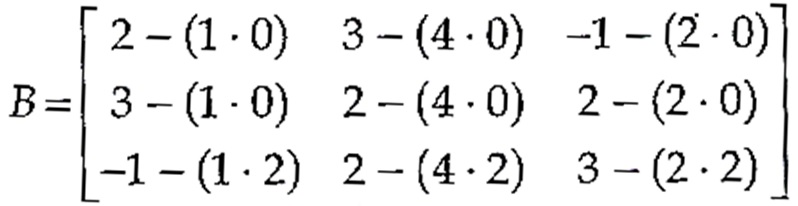
Então, B =  \left[ \begin{array}{ccc} 2 & 3 & -1\\ 3 & 2 & 2 \\ -3 & -6 & -1 \\ \end{array} \right] .

Finalmente, pela regra de Chió, $$ \text{det} (A) = (-1)^{2+4} \times \left| \begin{array}{ccc} 2 & 3 & -1\\ 3 & 2 & 2 \\ -3 & -6 & -1 \\ \end{array} \right| = 23.$$

OBSERVAÇÕES:

1. Para facilitar, quando aplicamos a regra de Chió para o elemento igual a 1, usamos a linha ou coluna com maior quantidade de zeros;
2. Quando a matriz não apresenta elemento igual a 1, podemos forçar o aparecimento usando manipulações algébricas entre linhas e colunas, usando o teorema de Jacobi, como fizemos anteriormente para a regra de Laplace.

Leia Mais Sobre Matrizes e Determinantes

• Matrizes – Definições Básicas e Primeiros Exemplos
• Os Principais Tipos de Matrizes
• A Adição de Matrizes
• A Multiplicação de Matrizes
• Inversão de Matrizes | Como calcular inversa de uma matriz?