Inversão de Matrizes | 9 Exercícios Resolvidos sobre Matriz Inversa

Aprenda a calcular a matriz inversa com esta lista de 9 exercícios resolvidos, seja utilizando a matriz adjunta ou o Método de Gauss-Jordan.

Uma matriz A, m \times n (lê-se: m por n), é uma tabela de m \cdot n números dispostos em m linhas e n colunas. Desta forma, representamos uma matriz colocando a tabela dentro de parênteses ou de colchetes, ou ladeado a tabela, à esquerda e à direita, por duas barras verticais, do seguinte modo: $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right] .$$

Uma matriz A, quadrada de ordem n, diz-se inversível se, e somente se, existir uma matriz B, quadrada de ordem n, tal que: $$A.B=B.A=Id_n.$$ A matriz B é denominada inversa de A e é indicada por A^{-1}.

OBSERVAÇÃO: 

1. Nenhum matriz nula é inversível;
2. Toda matriz identidade é inversível e igual à sua inversa;
3. Uma matriz é inversível se, e somente se, seu determinante é diferente de zero.
4. Uma matriz quadrada não inversível é chamada de matriz singular.

É possível provar que a matriz inversa de uma matriz A , caso exista, é dada por $$ A^{-1} = \frac{1}{\text{det} (A) } \left[ \text{cof} (A) \right]^{T}$$ onde \text{cof} (A) é a matriz formada pelos co-fatores de A . A matriz \left( \text{cof} (A) \right)^{T} é a matriz transposta da matriz dos cofatores, também chamada de matriz adjunta.

Outro método para encontrar a matriz inversa de A{n \times n} vem diretamente da definição que nos diz: $$A.A^{-1}=Id_n.$$ O método consiste em reduzir a matriz A à matriz identidade usando operações elementares entre linhas e aplicar a mesma sequência de operações elementares numa matriz identidade, para obter A^{-1} . Este método é chamado de Método de Gauss-Jordan.

Exercícios Resolvidos Sobre a Matriz Inversa

1) Utilize o Método de Gauss-Jordan para encontrar, se possível, a inversa das matrizes abaixo. Quando não for possível encontrar a matriz inversa, justifique.

a) A = \left[\begin{array}{cccc} 2& 1 & 1\\ 4 & -6 & 0\\ -2 & 7 & 2 \end{array} \right] ;

Solução:

Portanto a matriz inversa de A é a matriz A^{-1} = \left[\begin{array}{cccc}  \dfrac{3}{4} &- \dfrac{5}{16} & -\dfrac{3}{8}\\ & & \\ \dfrac{1}{2} & - \dfrac{3}{8}  & -\dfrac{1}{4} \\& & \\ - 1 & 1 & 1 \end{array} \right] .

b) B = \left[\begin{array}{cccc} 1 & 1 & 0\\ 0 & 1 & 1\\ 1 & 0 & 2 \end{array} \right] ;

Solução:

Portanto a matriz inversa de B é a matriz B^{-1} = \left[\begin{array}{cccc}  \dfrac{2}{3} &- \dfrac{2}{3} & \dfrac{1}{3}\\ & & \\ \dfrac{1}{3} & \dfrac{2}{3}  & -\dfrac{1}{3} \\& & \\ - \dfrac{1}{3} & \dfrac{1}{3} & \dfrac{1}{3} \end{array} \right] .

c) C = \left[\begin{array}{cccc} 1 & 2 & 6\\ 0 & 1 & 5\\ 2 & 3 & 7 \end{array} \right] ;

Solução:

O fato da matriz C ser equivalente a uma matriz com uma linha nula nos diz que ela não admite inversa.

d) D = \left[\begin{array}{cccc} 1 & 2 & 1\\ 0 & 1 & 2\\ 1 & 1 & 1 \end{array} \right] ;

Solução: 

Portanto a matriz inversa de D é a matriz D^{-1} = \left[\begin{array}{cccc} - \dfrac{1}{2} &- \dfrac{1}{2} & \dfrac{3}{2}\\ & & \\ 1 & 0 & -1 \\& & \\ - \dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{2} \end{array} \right] .

e) E = \left[\begin{array}{cccc} 1 & 2 & 2\\ 0 & 1 & 2\\ 1 & 3 & 4 \end{array} \right] ;

Solução:

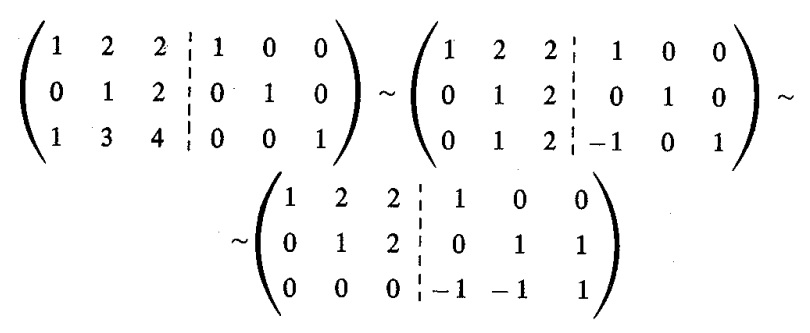
O fato da matriz E ser equivalente a uma matriz com uma linha nula nos diz que ela não admite inversa.

f) F = \left[\begin{array}{cccc} 1 & 1 & -1\\ 2 & 1 & 1\\ 3 & -1 & 1 \end{array} \right] ;

Solução: 

Portanto a matriz inversa de F é a matriz F^{-1} = \left[\begin{array}{cccc} \dfrac{1}{4} & 0 & \dfrac{1}{4}\\ & & \\ \dfrac{1}{8} & \dfrac{1}{2} & -\dfrac{3}{8} \\& & \\ - \dfrac{5}{8} & \dfrac{1}{2} & -\dfrac{1}{8} \end{array} \right] .

2) Mostre que o determinante da matriz $$ A = \left[ \begin{array}{cccc} a & b \\ c & d \\ \end{array} \right] $$ é igual $$ \text{det}(A) = ad – \; bc.$$ Em seguida, usando a Matriz Adjunta de A mostre que se \text{det} (A) \neq 0 , então $$ A^{-1} = \left[ \begin{array}{cccc} a & b \\ c & d \\ \end{array} \right]^{-1} =  \frac{1}{ad-bc} \left[ \begin{array}{cccc} d & -b \\ -c & a \\ \end{array} \right].$$

Solução: Observe que os cofatores  de $$ A = \left[ \begin{array}{cccc} a & b \\ c & d \\ \end{array} \right] $$ são todos dados por $$ A_{11} = d, \qquad A_{12} = -c, \qquad A_{21} = -b, \qquad A_{22} = a.$$ Usando a fórmula do determinante da matriz de ordem 2, sabemos que $$ \text{det}(A) = ad – \; bc.$$ Assim, como a matriz inversa de A é dada pela fórmula $$ A^{-1} = \frac{1}{ \text{det}(A) } \left[ \text{cof}(A)  \right]^{T}$$ então, podemos ver que $$ A^{-1} = \left[ \begin{array}{cccc} a & b \\ c & d \\ \end{array} \right]^{-1} =  \frac{1}{ad-bc} \left[ \begin{array}{cccc} d & -b \\ -c & a \\ \end{array} \right].$$

3) Explique porque a matriz $$ A = \left[ \begin{array}{cccc} 1 & 1 \\ 1 & 1 \\ \end{array} \right] $$ não admite inversa.

Solução: Como $$ \text{det}(A) = 0,$$ pois esta matriz tem duas linhas iguais, então podemos afirmar que esta é uma matriz singular, ou seja, não admite inversa.

4) Prove que dadas duas matrizes de mesma ordem, A e B , então \left( A.B \right)^{-1} = B^{-1} A^{-1}

Solução: Para mostrar que B^{-1} A^{-1} é a matriz inversa de A.B , nós multiplicamos as duas matrizes e aplicanos a propriedade associativa: $$  \left( A.B \right) . \left( B^{-1} A^{-1} \right) = A . B . B^{-1} . A^{-1} = A . Id . A^{-1} = A . A^{-1} = Id.$$ $$ \left( B^{-1} A^{-1} \right) . \left( A.B \right) = B^{-1} . A^{-1} . A . B . = B^{-1} . Id . B = B^{-1} . B = Id.$$ Portanto, pela definição de matriz inversa podemos afirmar que B^{-1} A^{-1} é a matriz inversa de A.B .

5) Uma matriz quadrada se diz ortogonal se é inversível e sua inversa é igual à sua transposta. Matematicamente, A é ortogonal se A^{-1} = A^{T} . Determine, se possível, x,y \in \mathbb{R} tal que a matriz  $$ A = \left[ \begin{array}{cccc} \sqrt{2} & x \\ y & \sqrt{2} \\ \end{array} \right]$$ seja ortogonal . Por fim, prove que o produto de duas matrizes ortogonais é ortogonal.

Solução: Suponha que a matriz $$ A = \left[ \begin{array}{cccc} \sqrt{2} & x \\ y & \sqrt{2} \\ \end{array} \right]$$ seja ortogonal. Logo, A^{-1} = A^{T} e aplicando a definição de função inversa teremos que $$ A \times A^{-1} = A \times A^{T} = ID_{2} \Leftrightarrow \\ \Leftrightarrow \left[ \begin{array}{cccc} \sqrt{2} & x \\ y & \sqrt{2} \\ \end{array} \right] \times \left[ \begin{array}{cccc} \sqrt{2} & y \\ x & \sqrt{2} \\ \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 \\ 0 & 1 \\ \end{array} \right] \Leftrightarrow \\ \Leftrightarrow \left[ \begin{array}{cccc} x^2 + 2 & \sqrt{2} y + \sqrt{2} x \\ \sqrt{2} y + \sqrt{2} x & y^2 +2 \\ \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 \\ 0 & 1 \\ \end{array} \right]$$ o que nos leva ao conjunto de equações $$ x^2 + 2 = 1 \Rightarrow x^2 = -1\\ \sqrt{2} y + \sqrt{2} x = 0 \\ y^2+2 = 1 \Rightarrow y^2 = -1.$$ Como não existem números reais que elevados ao quadrado resultem em um número negativo, não existem x,y \in \mathbb{R} tais que a matriz A seja ortogonal!

Agora, para provar que o produto de duas matrizes ortogonais é ortogonal vamos considerar duas matrizes ortogonais A e B , de ordem n . Sendo A e  B inversíveis, já vimos no exercício anterior que o produto A.B   também é inversível e que \left( A.B \right)^{-1} = B^{-1} A^{-1} . Daí, e lembrando que \left( A.B \right)^{T} = B^{T} A^{T} podemos concluir que $$ \left( A.B \right)^{-1} = B^{-1} A^{-1} = B^{T} A^{T} = \left( A.B \right)^{T}.$$

6) Determine a \in \mathbb{R} para que a matriz real A = \left[\begin{array}{cccc} 1 & 1 & 1\\ 2 & 1 & 2\\ 1 & 2 & a \end{array} \right] seja inversível.

Solução: Usando a Regra de Sarrus, podemos ver que $$ \text{det}(A) = 1-a.$$ Logo, para que esta matriz seja inversível, basta que este determinante seja diferente de zero, ou seja, que $$ a \neq 1. $$

7) Mostre que, se uma matriz é inversível, então \text{det} (A) \neq 0 .

Solução: Se a matriz A é inversível então A \times A^{-1} = Id . Pela propriedade de determinantes temos que $$ \text{det} (A \times A^{-1}) = \text{det} (Id) \Leftrightarrow \text{det} (A) \text{det} ( A^{-1}) = 1 .$$ Portanto, $$ \text{det} (A) \neq 0 \qquad \text{e} \qquad \text{det} (A^{-1}) \neq 0,$$ e, além disso, teremos que $$ \text{det} ( A^{-1}) = \frac{1}{\text{det} ( A)}.$$

8) Usando a Matriz Adjunta, calcule a inversa da matriz A = \left[\begin{array}{cccc} 1 & 2 & 4\\ 0 & 2 & 1\\ 3 & 1 & 2 \end{array} \right] .

Solução: Usando regra de Sarrus encontramos que  \text{det}(A) = \left|\begin{array}{cccc} 1 & 2 & 4\\ 0 & 2 & 1\\ 3 & 1 & 2 \end{array} \right| = -15 , logo esta matriz admite inversa. Sua matriz de cofatores sera dada por \text{cof}(A) = \left[\begin{array}{cccc} 3 & 0 & -6\\ 0 & -10 & 5\\ -6 & -1 & 2 \end{array} \right] . Desta forma, a matriz adjunta de A será dada por $$ \left[ \text{cof}(A) \right]^{T} = \left[\begin{array}{cccc} 3 & 0 & -6\\ 0 & -10 & -1\\ -6 & 5 & 2 \end{array} \right] .$$ Portanto, $$A^{-1} = \frac{1}{\text{det}(A)} =  \left[ \text{cof}(A) \right]^{T} = -\frac{1}{15} \left[\begin{array}{cccc} 3 & 0 & -6\\ 0 & -10 & -1\\ -6 & 5 & 2 \end{array} \right] = \left[\begin{array}{cccc} \frac{-1}{5} & 0 & \frac{2}{5 }\\ \frac{-1}{5} & \frac{2}{5} & \frac{1}{15}\\ \frac{2}{5} & \frac{-1}{3} & \frac{-2}{15} \end{array} \right].$$

9) Mostre que \left( A^{-1} \right)^{T} = \left( A^{T} \right)^{-1}

Solução: Da definição de matriz inversa temos que A \times A^{-1} = Id_{n} . Assim, pela propriedade da transposta da matriz produto, temos que $$ \left( A \times A^{-1} \right)^{T} = Id_{n}^{T} \Rightarrow \left( A^{-1} \right)^{T} \times A^{T} = Id_{n}.$$ Portanto, pela definição de matriz Inversa, a matriz \left( A^{-1} \right)^{T} é a inversa de A^{T} , e, por isso, podemos escrever que \left( A^{-1} \right)^{T} = \left( A^{T} \right)^{-1} .

Mais Listas de Exercícios sobre Matrizes

• Determinantes | 1ª Lista de Exercícios Resolvidos
• Multiplicação de Matrizes | 1ª Lista de Exercícios Resolvidos
• Adição de Matrizes | 1ª Lista de Exercícios Resolvidos
• Introdução às Matrizes: 1ª Lista de Exercícios Resolvidos

Leia Mais sobre Matrizes:

• Como Somar Matrizes? Um guia passo a passo com exemplos
• Como multiplicar matrizes? Um guia passo a passo com exemplos
• Inversão de Matrizes | Como calcular inversa de uma matriz?
• Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió