Multiplicação de Matrizes | 1ª Lista de Exercícios Resolvidos

Dez exercícios resolvidos para você entender de vez o processo que envolve a multiplicação, ou o produto, de duas matrizes.

Uma matriz A, m \times n (lê-se: m por n), é uma tabela de m \cdot n números dispostos em m linhas e n colunas. Desta forma, representamos uma matriz colocando a tabela dentro de parênteses ou de colchetes, ou ladeado a tabela, à esquerda e à direita, por duas barras verticais, do seguinte modo: $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right] .$$

Para que duas matrizes sejam compatíveis para multiplicação, o número de colunas na primeira matriz deve ser igual ao número de linhas na segunda matriz. Ao realizar a multiplicação de matrizes, cada elemento em uma matriz é multiplicado por todos os elementos na outra matriz e, em seguida, somados para formar um valor resultante para essa posição na matriz de saída. Mas antes, vamos falar sobre o produto de um escalar por uma matriz.

Assim se A = (a_{ij})_{m×p} e B = (b_{ij})_{p×n} o produto entre A e B é definido pela matriz de ordem m × n $$C = AB$$ obtida da seguinte forma: $$c_{ij} = a_{i1} b_{1j} + a_{i2} b_{2j} + . . . + a_{ip} b_{pj},$$ para i = 1, . . . ,m e j = 1, . . . , n.

Matricialmente, temos que:

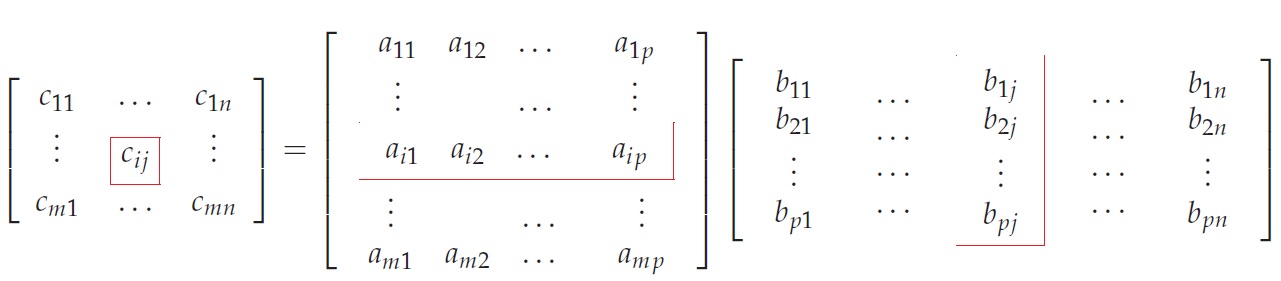
OBSERVAÇÕES: 

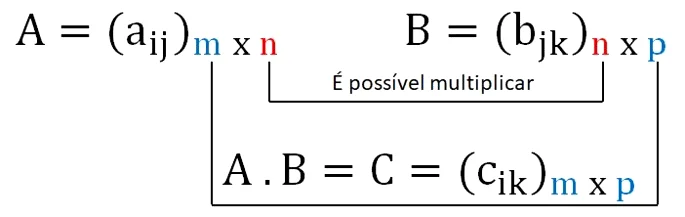
1. Pela definição podemos concluir que o produto de duas matrizes só existe quando o número de colunas da primeira matriz é igual ao número de linhas da segunda matriz;
2. Podemos concluir que o número de linhas da matriz-produto é igual ao número de linhas da primeira matriz e o número de colunas da matriz-produto é o número de colunas da segunda matriz;

A imagem abaixo ilustra estas duas observações quanto ao produto de matrizes:

Exercícios Resolvidos Sobre Multiplicação de Matrizes:

1) Dadas das matrizes A=\left[ \begin{array}{cccc} 0 & -2 \\ 1 & 3 \\ \end{array} \right] e B=\left[ \begin{array}{cccc} 4 & 3 \\ 0 & 1 \\ \end{array} \right], obter as matrizes produto A \times B e B \times A , caso existam.

SOLUÇÃO: Como as matrizes em questão são todas quadradas de ordem 2, podemos garantir a existência dos produtos A \times B e B \times A que são dados por $$ A \times B = \left[ \begin{array}{cccc} 0 & -2 \\ 1 & 3 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 4 & 3 \\ 0 & 1 \\ \end{array} \right] = \left[ \begin{array}{cccc} 0 \times 4 + (-2) \times 0 & 0 \times 3 + (-2) \times 1 \\ 1 \times 4 + 3 \times 0 & 1 \times 3 + 3 \times 1 \end{array} \right] = \left[ \begin{array}{cccc} 0 & -2 \\ 4 & 6 \\ \end{array} \right]$$ e $$ B \times A =  \left[ \begin{array}{cccc} 4 & 3 \\ 0 & 1 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 0 & -2 \\ 1 & 3 \\ \end{array} \right] = \left[ \begin{array}{cccc} 4 \times 0 + 3 \times 1 & 4 \times (-2) + 3 \times 3 \\ 0 \times 0 + 1 \times 1 & 0 \times (-2) + 1 \times 3 \\ \end{array} \right] = \left[ \begin{array}{cccc} 3 & 1 \\ 1 & 3 \\ \end{array} \right]$$

OBSERVAÇÃO SOBRE O EXERCÍCIO 1: Note que a multiplicação de matrizes não é comutativa, isto é, pode existir A \times B e B \times A e ainda A \times B \neq B \times A . Caso aconteça A \times B = B \times A , dizemos que A e B são matrizes comutáveis.

2) Dadas das matrizes A=\left[ \begin{array}{cccc} 2 & 0 \\ 2 & 0 \\ \end{array} \right] e B=\left[ \begin{array}{cccc} 0 & 0 \\ 2 & 2 \\ \end{array} \right], obter as matrizes produto A \times B e B \times A , caso existam.

SOLUÇÃO: $$ A \times B = \left[ \begin{array}{cccc} 2 & 0 \\ 2 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 0 & 0 \\ 2 & 2 \\ \end{array} \right] = \left[ \begin{array}{cccc} 2 \times 0 + 0 \times 2 & 2 \times 0 + 0 \times 2 \\ 2 \times 0 + 0 \times 2 & 2 \times 0 + 0 \times 2 \\ \end{array} \right] = \left[ \begin{array}{cccc} 0 & 0 \\ 0 & 0 \\ \end{array} \right].$$

OBSERVAÇÃO SOBRE O EXERCÍCIO 2: o produto de duas matrizes não-nulas pode resultar em uma matriz nula. Portanto, se A e B são matrizes de A \times B = 0 , nem sempre é verdade que A = 0 ou B = 0 .

3) Dadas das matrizes A=\left[ \begin{array}{cccc} 1 & 2 \\ 2 & 4 \\ \end{array} \right], B=\left[ \begin{array}{cccc} 0 & -3 \\ 1 & -1 \\ \end{array} \right] e C=\left[ \begin{array}{cccc} 2 & -1 \\ 0 & -2 \\ \end{array} \right], obter as matrizes A \times B e A \times C , caso existam.

SOLUÇÃO: Note que neste exercício temos A \times B = A \times C , porém B \neq C . De fato,  $$ A \times B = \left[ \begin{array}{cccc} 1 & 2 \\ 2 & 4 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 0 & -3 \\ 1 & -1 \\ \end{array} \right] = \left[ \begin{array}{cccc} 2 & -5 \\ 4 & -10 \\ \end{array} \right]$$ $$ A \times C = \left[ \begin{array}{cccc} 1 & 2 \\ 2 & 4 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 2 & -1 \\ 0 & -2 \\ \end{array} \right] = \left[ \begin{array}{cccc} 2 & -5 \\ 4 & -10 \\ \end{array} \right].$$

OBSERVAÇÃO SOBRE O EXERCÍCIO 3: A lei do cancelamento para a multiplicação nem sempre é válida para as matrizes. Assim, se A \times B = A \times C não se significa que [/katex] B = C [/katex].

4) Sendo A=\left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] e B=\left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right], determine:

a) \left(A+B \right) ^2 ;

SOLUÇÃO: Como $$ A + B = \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] + \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] = \left[ \begin{array}{cccc} 4 & 1 \\ 5 & 4 \\ \end{array} \right],$$ então $$ \left(A+B \right) ^2 = \left( \left[ \begin{array}{cccc} 4 & 1 \\ 5 & 4 \\ \end{array} \right] \right) ^2 = \left[ \begin{array}{cccc} 4 & 1 \\ 5 & 4 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 4 & 1 \\ 5 & 4 \\ \end{array} \right] = \left[ \begin{array}{cccc} 21 & 8 \\ 40 & 21 \\ \end{array} \right]$$

b) A^2 + 2 \cdot A \times B + B^2;

SOLUÇÃO: Como $$ A^2 = \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] = \left[ \begin{array}{cccc} 7 & 2 \\ 3 & 6 \\ \end{array} \right], $$ $$ A \times B = \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] = \left[ \begin{array}{cccc} 7 & 7 \\ 9 & -3 \\ \end{array} \right] $$ e $$ B^2 = \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] = \left[ \begin{array}{cccc} 7 & -7 \\ 14 & 14 \\ \end{array} \right],$$ então $$ A^2 + 2 \cdot A \times B + B^2 = \left[ \begin{array}{cccc} 7 & 2 \\ 3 & 6 \\ \end{array} \right] + 2 \times \left[ \begin{array}{cccc} 7 & 7 \\ 9 & -3 \\ \end{array} \right] + \left[ \begin{array}{cccc} 7 & -7 \\ 14 & 14 \\ \end{array} \right] = \\ = \left[ \begin{array}{cccc} 7 & 2 \\ 3 & 6 \\ \end{array} \right] + \left[ \begin{array}{cccc} 14 & 14 \\ 18 & -6 \\ \end{array} \right] + \left[ \begin{array}{cccc} 7 & -7 \\ 14 & 14 \\ \end{array} \right] = \left[ \begin{array}{cccc} 28 & 9 \\ 35 & 14 \\ \end{array} \right] $$

c) A^2 +  A \times B + B \times A + B^2;

SOLUÇÃO: Como $$ A^2 = \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] = \left[ \begin{array}{cccc} 7 & 2 \\ 3 & 6 \\ \end{array} \right], $$ $$ A \times B = \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] = \left[ \begin{array}{cccc} 7 & 7 \\ 9 & -3 \\ \end{array} \right], $$ $$ B \times A =  \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] = \left[ \begin{array}{cccc} 0 & 6 \\ 14 & 4 \\ \end{array} \right]$$ e $$ B^2 = \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 3 & -1 \\ 2 & 4 \\ \end{array} \right] = \left[ \begin{array}{cccc} 7 & -7 \\ 14 & 14 \\ \end{array} \right],$$ então $$ A^2 +  A \times B + B \times A + B^2 = \left[ \begin{array}{cccc} 7 & 2 \\ 3 & 6 \\ \end{array} \right] + \times \left[ \begin{array}{cccc} 7 & 7 \\ 9 & -3 \\ \end{array} \right] + \left[ \begin{array}{cccc} 0 & 6 \\ 14 & 4 \\ \end{array} \right] +\left[ \begin{array}{cccc} 7 & -7 \\ 14 & 14 \\ \end{array} \right] = \left[ \begin{array}{cccc} 21 & 8 \\ 40 & 21 \\ \end{array} \right]$$

OBSERVAÇÃO SOBRE O EXERCÍCIO 4: Note que as relações de produtos notáveis para números reais, como o quadrado da soma ou da diferença, nem sempre podem ser garantidos para matrizes. Isto é (A+B)^{2} = A^2 +  A \times B + B \times A + B^2 \neq A^2 +2 \times A \times B + B^2 . Apenas se as matrizes A e B forem comutativas, ou seja, se A \times B = B \times A , podemos garantir que (A+B)^{2} = A^2 +  2 \times A \times B + B^2 .

5) Sendo A=\left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] e B=\left[ \begin{array}{cccc} -1 & 3 \\ 2 & 1 \\ \end{array} \right], determine:

a) \left(A \times B \right) ^T ;

SOLUÇÃO: Como $$A \times B = \left[ \begin{array}{cccc} 1 & 2 \\ 3 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} -1 & 3 \\ 2 & 1 \\ \end{array} \right] = \left[ \begin{array}{cccc} 3 & 5 \\ -3 & 9 \\ \end{array} \right]$$ então $$ \left( A \times B \right)^{T} =\left( \left[ \begin{array}{cccc} 3 & 5 \\ -3 & 9 \\ \end{array} \right] \right)^{T} = \left[ \begin{array}{cccc} 3 & -3 \\ 5 & 9 \\ \end{array} \right].$$

b) A^T \times B^T ;

SOLUÇÃO: Como A^{T} =\left[ \begin{array}{cccc} 1 & 3 \\ 2 & 0 \\ \end{array} \right] e B^{T}=\left[ \begin{array}{cccc} -1 & 2 \\ 3 & 1 \\ \end{array} \right], então $$ A^T \times B^T =  \left[ \begin{array}{cccc} 1 & 3 \\ 2 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} -1 & 2 \\ 3 & 1 \\ \end{array} \right] = \left[ \begin{array}{cccc} 8 & 5 \\ -2 & 4 \\ \end{array} \right]$$

c) B^T  \times A^T;

SOLUÇÃO: Como A^{T} =\left[ \begin{array}{cccc} 1 & 3 \\ 2 & 0 \\ \end{array} \right] e B^{T}=\left[ \begin{array}{cccc} -1 & 2 \\ 3 & 1 \\ \end{array} \right], então $$ B^T \times A^T =  \left[ \begin{array}{cccc} -1 & 2 \\ 3 & 1 \\ \end{array} \right] \times \left[ \begin{array}{cccc} 1 & 3 \\ 2 & 0 \\ \end{array} \right] = \left[ \begin{array}{cccc} 3 & -3 \\ 5 & 9 \\ \end{array} \right]$$

OBSERVAÇÃO SOBRE O EXERCÍCIO 5: Note que \left(A \times B \right) ^T \neq A^T \times B^T e \left(A \times B \right) ^T = B^T  \times A^T.

6) Mostre que:

a) Dada uma matriz A_{m \times n} , então \left( \alpha \cdot A_{m \times n} \right)^{T} = \alpha \cdot A_{m \times n}^{T};

SOLUÇÃO: Seja A \in \mathbb{M}_{m \times n} , dada por $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right]$$ e \alpha \in \mathbb{R} , temos, por definição, que $$ \alpha \cdot A = \left[ \begin{array}{cccc} \alpha a_{11} & \alpha a_{12} & \ldots & \alpha a_{1n} \\ \alpha a_{21} & \alpha a_{22} & \ldots & \alpha a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ \alpha a_{m1} & \alpha a_{m2} & \cdots & \alpha a_{mn}\\ \end{array} \right] .$$ Desta forma, $$ \left( \alpha \cdot A \right)^{T} = \left[ \begin{array}{cccc} \alpha a_{11} & \alpha a_{21} & \ldots & \alpha a_{m1} \\ \alpha a_{12} & \alpha a_{22} & \ldots & \alpha a_{2m} \\ \vdots & \ddots & \cdots & \vdots \\ \alpha a_{1n} & \alpha a_{2n} & \cdots & \alpha a_{mn}\\ \end{array} \right]  = \alpha \cdot \left[ \begin{array}{cccc}  a_{11} &  a_{21} & \ldots & a_{m1} \\  a_{12} &  a_{22} & \ldots &  a_{2m} \\ \vdots & \ddots & \cdots & \vdots \\  a_{1n} &  a_{2n} & \cdots &  a_{mn}\\ \end{array} \right] = \alpha \cdot A^T$$

b) Dadas as matrizes A e B , então \left( A \times B \right)^{T} = B^{T} \times A^{T};

SOLUÇÃO:  Sejam A = \left( a_{ij} \right), A^{T} = \left( b_{ji} \right), B = \left( c_{jk} \right) e B^T = \left( d_{kj} \right) . Então b_{ji} = a_{ij} e d_{kj} = c_{jk} . Supondo A \times B = \left( r_{jk} \right) e B^{T} \times A^{T} = \left( s_{kj} \right) temos que $$ r_{jk} = \sum\limits_{j=1}^{n}{a_{ij}c_{jk} } = \sum\limits_{j=1}^{n}{b_{ji}d_{kj} } = s_{ki}$$ o que mostra que de fato \left( A \times B \right)^{T} = B^{T} \times A^{T}.

c) Se A \times B = B \times A, então A e B precisam ser matrizes quadradas de mesma ordem.

SOLUÇÃO: Sejam A_{m \times n } e B_{p \times q } tais que os produtos A _{m \times n } \times B_{p \times q } e B_{p \times q } \times A_{m \times n } existam, então, pela regra do produto de matrizes, precisamos que n = p e m = q . Logo, precisamos ter matrizes A_{m \times n } e B_{n \times m } . Desta forma, a matriz produto A \times B é uma matriz m \times m e a matriz produto B \times A é uma matriz n \times n . Por fim, para que A \times B = B \times A a duas matrizes produto precisam ter o mesmo número de linhas e colunas, portanto, devemos ter m = n , mostrando o que se pede.

7) Determine todas as matrizes que comutam com a matriz $$ A=\left[ \begin{array}{cccc} 1 & 1 \\ 0 & 0 \\ \end{array} \right],$$ ou seja, todas as matrizes X_{2 \times 2} tais que A \times X = X \times A .

SOLUÇÃO: Suponhamos X=\left[ \begin{array}{cccc} x & y \\ z & t \\ \end{array} \right] . Então: $$ A \times X = X \times A \Leftrightarrow \left[ \begin{array}{cccc} 1 & 1 \\ 0 & 0 \\ \end{array} \right] \times \left[ \begin{array}{cccc} x & y \\ z & t \\ \end{array} \right] = \left[ \begin{array}{cccc} x & y \\ z & t \\ \end{array} \right] \times \left[ \begin{array}{cccc} 1 & 1 \\ 0 & 0 \\ \end{array} \right] \Leftrightarrow \left\{ \begin{array}{rll} x+z & = & x \\ y+t &=& x \\ 0 & = & z \end{array} \right. $$ Logo X=\left[ \begin{array}{cccc} x & y \\ 0 & x-y \\ \end{array} \right] onde x e y são números quaisquer.

8) Dada a matriz $$ A=\left[ \begin{array}{cccc} 2 & 1 \\ 1 & 1 \\ \end{array} \right],$$ determine uma matriz X_{2 \times 2} tal que A \times X = Id_{2} .

SOLUÇÃO: Fazendo X=\left[ \begin{array}{cccc} x & y \\ z & t \\ \end{array} \right] , queremos resolver a equação matricial $$ \left[ \begin{array}{cccc} 2 & 1 \\ 1 & 1 \\ \end{array} \right] \times \left[ \begin{array}{cccc} x & y \\ z & t \\ \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 \\ 0 & 1 \\ \end{array} \right] \Leftrightarrow  \\ \Leftrightarrow \left[ \begin{array}{cccc} 2x + z & 2y + t \\ x + z & y + t \\ \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 \\ 0 & 1 \\ \end{array} \right] $$ o que nos leva aos sistemas lineares $$ \left\{ \begin{array}{rll} 2x+z & = & 1 \\ x +z &=& 0 \end{array} \right.  \qquad \text{e} \qquad \left\{ \begin{array}{rll} y+t & = & 1 \\ 2y+t &=& 0 \end{array} \right.  $$ que nos dá soluções $$ x = 1;\qquad y = -1; \qquad z = -1\ \qquad t= 2 .$$ Portanto, X=\left[ \begin{array}{cccc} 1 & -1 \\ -1 & 2 \\ \end{array} \right] .

9) Resolva a equação matricial A \times X = B , onde A = \left[ \begin{array}{cccc} 2 & 3 \\ -3 & 6 \\ \end{array} \right] e B = \left[ \begin{array}{cccc} 5 & 3 \\ -4 & 13 \\ \end{array} \right] .

SOLUÇÃO: Pela definição da multiplicação de matrizes precisamos encontrar uma matriz X , quadrada e de ordem 2. Fazendo X=\left[ \begin{array}{cccc} m & n \\ p & q \\ \end{array} \right] e substituindo na equação matricial A \times X = B , encontramos $$ \left[ \begin{array}{cccc} 2 & 3 \\ -3 & 6 \\ \end{array} \right] \times \left[ \begin{array}{cccc} m & n \\ p & q \\ \end{array} \right] = \left[ \begin{array}{cccc} 5 & 3 \\ -4 & 13 \\ \end{array} \right] \Rightarrow \left[ \begin{array}{cccc} 2m +3p & 3n+3q \\ -3m + 6p & -3n + 6q \\ \end{array} \right] = \left[ \begin{array}{cccc} 5 & 3 \\ -4 & 13 \\ \end{array} \right]$$ o que nos leva aos sistemas lineares de ordem 2 : $$ \left\{ \begin{array}{rll} 3m + 3p & = & 5 \\ -3m + 6p &=& -4 \end{array} \right.  \qquad \text{e} \qquad \left\{ \begin{array}{rll} 2n + 3q & = & 3 \\ -3n + 6q  &=& 13 \end{array} \right.  $$ que nos dá soluções $$ m=2;\qquad n = -1; \qquad p = \frac{1}{3}\ \qquad q = \frac{5}{3} .$$ Portanto, X=\left[ \begin{array}{cccc} 2 & -1 \\ \dfrac{1}{3} & \dfrac{5}{3} \\ \end{array} \right] .

10) Determine x e y reais para que A^2 = B , onde A = \left[ \begin{array}{cccc} x & 1 \\ 1 & y \\ \end{array} \right] e B = \left[ \begin{array}{cccc} 5 & 1 \\ 1 & 2 \\ \end{array} \right] .

SOLUÇÃO: $$ A^2 = B \Leftrightarrow A \times A = B \Leftrightarrow \left[ \begin{array}{cccc} x & 1 \\ 1 & y \\ \end{array} \right] \times \left[ \begin{array}{cccc} x & 1 \\ 1 & y \\ \end{array} \right] = \left[ \begin{array}{cccc} 5 & 1 \\ 1 & 2 \\ \end{array} \right]  \Leftrightarrow \\ \Leftrightarrow \left[ \begin{array}{cccc} x^2 +1 & x+y\\ x+y & 1+ y^2 \\ \end{array} \right] = \left[ \begin{array}{cccc} 5 & 1 \\ 1 & 2 \\ \end{array} \right] $$ o que nos leva ao sistema de equações não-lineares $$ \left\{ \begin{array}{rll} x^2 +1 & = & 5 \Leftrightarrow x = \pm 2\\ x + y &=& 1 \\ 1 + y^2 & = & 2 \Leftrightarrow x = \pm 1 \\ \end{array} \right.  $$ Observe que os pares (x,y) = (2,1) , (x,y) = (-2,1) e (x,y) = (-2,-1) não satifazem a segunda equação x+y = 1 . Apenas o par (x,y) = (2,-1) satisfaz esta equação especificamente. Portanto, x =2  e y = -1  .

Mais Listas de Exercícios sobre Matrizes

• Determinantes | 1ª Lista de Exercícios Resolvidos
• Adição de Matrizes | 1ª Lista de Exercícios Resolvidos
• Introdução às Matrizes: 1ª Lista de Exercícios Resolvidos

Leia Mais sobre Matrizes:

• Como Somar Matrizes? Um guia passo a passo com exemplos
• Como multiplicar matrizes? Um guia passo a passo com exemplos
• Inversão de Matrizes | Como calcular inversa de uma matriz?
• Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió