Vetores no Plano Cartesiano – 1ª Lista de Exercícios Resolvidos

Esta lista de exercícios resolvidos é perfeita para você que quer entender os vetores (norma e produto escalar) no plano cartesiano através de problemas que irão refinar seu raciocínio lógico em geometria analítica.

Fixada a base canônica \left\{ \vec{i} , \vec{j} \right\}, fica estabelecida uma correspondência biunívoca entre os vetores do plano e os pares ordenados (x,y) de números reais. Nestas condições definimos um vetor no plano como um par ordenado (x,y) de números reais representado por \vec{v} = (x,y) que é a expressão analítica de \vec{v} . A primeira componente x é chamada abscissa e a segunda, ordenada.

Desta forma, o plano cartesiano pode ser encarado como um conjunto de pontos ou um conjunto de vetores.

Dado um ponto P( x, y) , o comprimento do segmento de reta \overline{OP} é, como sabemos (por este artigo), igual a $$ \sqrt{x^2 + y^2} .$$ Diremos também que este é o comprimento do vetor \vec{OP} e escrevemos $$ | \vec{v} | = | \vec{OP} | = | (x,y)| = \sqrt{x^2 + y^2} .$$ Se | \vec{v} | = 1 então diremos que \vec{v} é um vetor unitário.

Chama-se produto escalar (ou produto interno usual) de dois vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} \qquad \text{e} \qquad \vec{v} = x_2 \vec{i} + y_2 \vec{j} $$ e se representa por \vec{u} \cdot \vec{v} , ao número real $$  \vec{u} \cdot \vec{v} = x_1 x_2 + y_1 y_2 .$$ O produto escalar de \vec{u} por \vec{v} também é indicado por \langle \vec{u} , \vec{v} \rangle e se lê ” \vec{u} escalar \vec{v} “. Observando que $$ \vec{v} \cdot \vec{v} = x^2 + y^2 $$ então podemos escrever que $$ | \vec{v} |= \sqrt{ \vec{v} \cdot \vec{v} }.$$

Se \theta é o ângulo entre os vetores \vec{u} e \vec{v} , então \vec{u} \cdot \vec{v} =| \vec{u} | | \vec{v} | \text{cos} ( \theta ) . Daí podemos concluir que o ângulo entre os vetores \vec{u} e \vec{v} é dado por $$ \theta = \text{arc cos}\left( \frac{\vec{u} \cdot \vec{v}}{| \vec{u} | | \vec{v} |} \right).$$ Os vetores \vec{u} e \vec{v} são perpendiculares se, e somente se, \vec{u} \cdot \vec{v} = 0 .

Sejam \vec{u} e \vec{v} , ambos vetores não-nulos, e \theta o ângulo formado entre eles. Então o vetor $$ \vec{w} = \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} $$ é a projeção de \vec{u} sobre \vec{v} . A notação usual da a projeção de \vec{u} sobre \vec{v} é dada por $$ \text{proj}_{\vec{v}} \vec{u} =  \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} = \left( \frac{\vec{u} \cdot \vec{v}}{\vec{v} \cdot \vec{v}} \right) \vec{v}$$  e esta projeção de vetores é representada nas figuras abaixo.

Considerando o paralelogramo ABCD no plano. Colocando \vec{AB} = \vec{v} = (\alpha , \beta ) e \vec{AC} = \vec{v} = ( \gamma , \delta ). A área do paralelogramo é dada pelo módulo do determinante $$ \left|\begin{array}{cc} \alpha & \gamma \\ \beta & \delta \\ \end{array} \right| = \alpha \delta – \beta \gamma$$ ou seja, $$ \text{área de ABCD} =  | \alpha \delta – \beta \gamma | .$$

Considerando, agora, o triângulo com vértices A\left( x_1 , y_1\right) , B\left( x_2 , y_2\right) e C\left( x_3 , y_3\right) . A área do triângulo ABC é a metade da área do paralelogramo ABCD . Portanto, $$ \text{área de ABC} = \frac{1}{2} |D|, \qquad \text{onde } D = \left|\begin{array}{cccc} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{array} \right|.$$

1ª Lista de Exercícios Resolvidos sobre Vetores no Plano

1) Determinar a extremidade do segmento que representa o vetor \vec{v} = (2,-5) , sabendo que sua origem é o ponto A(-1,3) .

SOLUÇÃO: Sabendo que \vec{v} = B - A onde o ponto B(x,y) representa a extremidade procurada temos então que $$ (2,-5) = (x,y) – (-1,3) $$. Logo, $$ x+1 = 2 \Rightarrow x = 1 \\ y -3 = -5 \Rightarrow y = -2 .$$ Portanto, a extremidade do vetor \vec{v} é o ponto B(1,-2) .

2) Determine \alpha para que o vetor \vec{v} = \left( \alpha, -\dfrac{1}{2} \right) seja unitário.

SOLUÇÃO: Para que o vetor \vec{v} = \left( \alpha, -\dfrac{1}{2} \right) seja unitário sua norma deve ser igual a 1. Desta forma $$ \left| \vec{v} \right| = \sqrt{\alpha^2 + \frac{1}{4}} =1 .$$ Daí, $$ \alpha^2 + \frac{1}{4} = 1 \Rightarrow \alpha^2 = \frac{3}{4} \Rightarrow \alpha = \pm \frac{\sqrt{3}}{2}.$$

3) Sabendo que o vetor \vec{v} = (2,1) forma um ângulo de 60º com o vetor \vec{AB} determinado pelos pontos A(3,1) e B(4,m) , determine, se possível, calcular m .

SOLUÇÃO: Pela fórmula do ângulo entre dois vetores podemos escrever $$\text{cos} \left( \frac{\pi}{3} \right) = \frac{\vec{u} \cdot \vec{AB}}{| \vec{u} | | \vec{AB} |}.$$ Observe que:

• \vec{AB} = B - A = (4,m) - (3,1) = (1, m-1) ;
• | \vec{u} | = \sqrt{2^2 + 1^2} = \sqrt{5} ;
• | \vec{AB} | = \sqrt{1^2 + (m-1)^2} = \sqrt{m^2 -2m+2} ;
• \vec{AB} \cdot \vec{v} = (1, m-1) \cdot (2,1) = 2+ (m-1) = m+1 .

Assim, $$\text{cos} \left( \frac{\pi}{3} \right) = \frac{\vec{u} \cdot \vec{AB}}{| \vec{u} | | \vec{AB} |} \Rightarrow\frac{1}{2} = \frac{m+1}{ \sqrt{5} \sqrt{m^2 -2m+2} }.$$ Daí, $$ \sqrt{5} \sqrt{m^2 -2m+2} = 2 (m+1) \\ 5 (m^2 -2m +2) = 4(m^2 +2m +1) \\ m^2 -18m +6 = 0  \Rightarrow m = 9 \pm 5 \sqrt{3}.$$

4) Determine os ângulos internos ao triângulo ABC , sendo A(3,-3) , B(2,-1) e C(1,0) .

SOLUÇÃO: Primeiramente considere a representação deste triângulo no plano cartesiano:

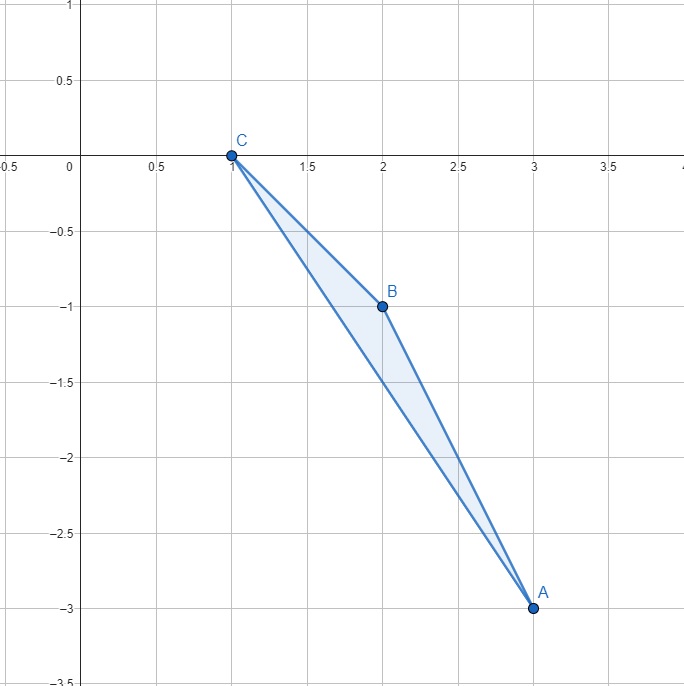
Observemos que o ângulo  é o ângulo entre os vetores \vec{AB} e \vec{AC} , logo: $$ \text{cos} \left( \right) = \frac{\vec{AB} \cdot \vec{AC}}{| \vec{AB} | | \vec{AC} |} .$$ Como

• | \vec{AB} | = \sqrt{(2-3)^2 + (-1+3)^2} = \sqrt{1+4} = \sqrt{5};
• | \vec{AC} | = \sqrt{(1-3)^2 + (0+3)^2} = \sqrt{4 + 9} = \sqrt{13} ;
• \vec{AB} \cdot \vec{AC} = (-1,2) \cdot (-2,3) = 2+6 = 8 .

obteremos $$ \text{cos} \left(Â \right) = \frac{8}{\sqrt{5} \sqrt{13}} .$$ Ou seja, $$ Â = \text{arc cos} \left( \frac{8}{\sqrt{5} \sqrt{13}} \right) $$

Agora, observemos que o ângulo B é o ângulo entre os vetores \vec{BA} e \vec{BC} , logo: $$ \text{cos} \left( B \right) = \frac{\vec{BA} \cdot \vec{BC}}{| \vec{BA} | | \vec{BC} |} .$$ Como

• | \vec{BA} | = | \vec{AB} | = \sqrt{5};
• | \vec{BC} | = \sqrt{(1-2)^2 + (0+1)^2} = \sqrt{1 +1} = \sqrt{2} ;
• \vec{BA} \cdot \vec{BC} = (1,-2) \cdot (-1,1) = -1-2 = -3 .

obteremos $$ \text{cos} \left(B \right) = \frac{-3}{\sqrt{5} \sqrt{2}} .$$ Ou seja, $$ B = \text{arc cos} \left( \frac{-3}{\sqrt{5} \sqrt{2}} \right) $$

Como a soma dos ângulos internos de um triângulo é igual a 180º, podemos afirma que o ângulo C é dado por $$ C = 180º – \text{arc cos} \left( \frac{-3}{\sqrt{5} \sqrt{2}} \right)  – \text{arc cos} \left( \frac{8}{\sqrt{5} \sqrt{13}} \right).$$

5) O centro de gravidade G de uma barra homogênea que pode ser representada pelo segmento AB presa pela extremidade A ao ponto A e tendo extremidade B sustentada por um apoio – situa-se sobre o ponto (5,3) . Retirado o apoio, a barra cai em direção ao solo, representado pelo eixo das abscissas e representado pela figura abaixo. Determine as coordenadas das duas posições da extremidade B (antes e depois da retirada do apoio).

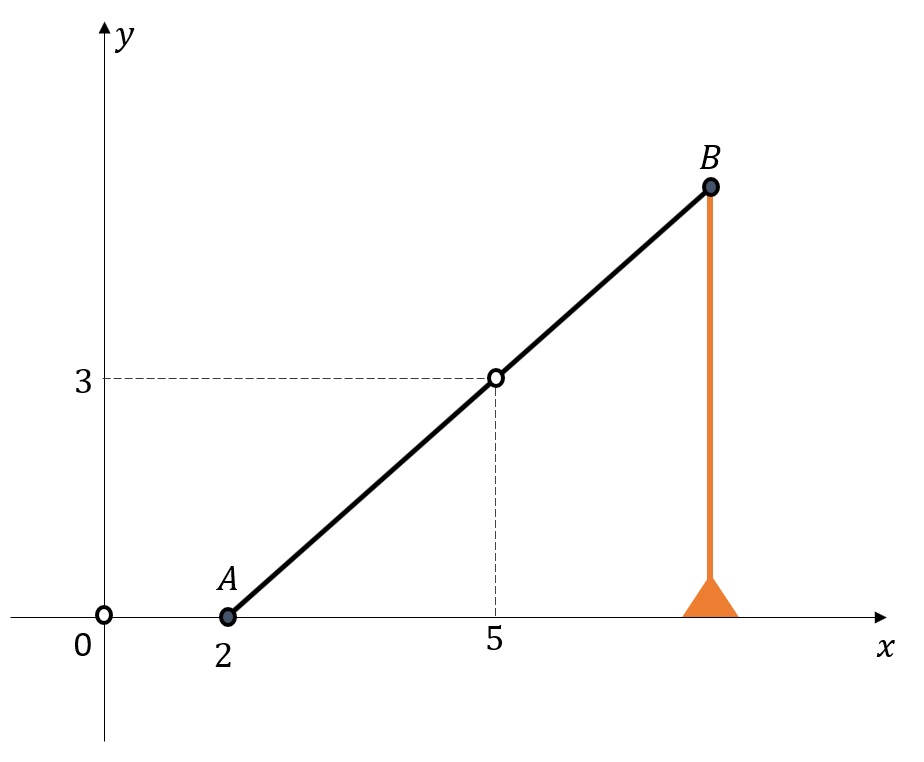
SOLUÇÃO: Antes da queda, (5,3) é o ponto médio entre (2,0) e B \left( x_B , y_B \right) . Assim: $$ 5 = \frac{x_B + 2}{2} \Rightarrow x_B = 8 \\ 3 = \frac{y_B + 0}{2} \Rightarrow y_B = 6 .$$ Logo, B\left( x_B , y_B \right) = B(8,6)  . O comprimentos da barra é $$ d(A,B) = \sqrt{(8-2)^2 + (6-0)^2} = 6 \sqrt{2}.$$ Após a queda, a extremidade móvel ocupa a posição $$ \left(2 + 6 \sqrt{2}, 0 \right).$$

6) Dentre os pontos que equidistam de A(1,2) e B(3,4) , qual o mais próximo de P(4,3) ?

SOLUÇÃO: Considere X (x,y) como o ponto procurado. Primeiramente, precisamos que $$ d(A,X) = d(B,X).$$ Daí, $$ d(A,X) ^2 = d(B,X) ^2 \Rightarrow (x-1)^2 + (y-2)^2 = (x-3)^2+(y-4)^2 \\ x^2 – 2x +1 +y^2 – 4 y + 4 = x^2 -6x +9 +y^2 – 8y +16 \\ -2x-4y+4 = -6x-8y+25 \\ 4y = -4x +21 \Rightarrow y = -x +\frac{21}{4} .$$ Logo, os pontos que equidistam de A e B são de forma \left( x, x-\frac{21}{4} \right) . Aquele que está mais próximo de P(4,3) é o ponto de mínimo da função $$ d(P,X) = \sqrt{(x-4)^2 + \left(-x+\frac{21}{4} – 3 \right)^2}  = \sqrt{2x^2-\frac{25}{2} x + \frac{337}{16} }$$ Obviamente, o ponto com a menor distância a P(4,3) também tem a menor distância ao quadrado. Assim, o ponto que queremos é aquele que tem coordenada x igual ao do ponto de mínimo da função $$d(x) = 2x^2-\frac{25}{2} x + \frac{337}{16} ,$$ que é dado por $$ V =  \left( \frac{31}{10} , \frac{3}{2} \right) .$$  Portanto, dentre os pontos que equidistam de A(1,2) e B(3,4) o mais próximo de P(4,3) é X \left(\frac{31}{10},-\frac{31}{10} +\frac{21}{4} \right) , ou seja, X\left(\dfrac{31}{10}, \dfrac{43}{20} \right) . A ilustração abaixo representa todo este processo:

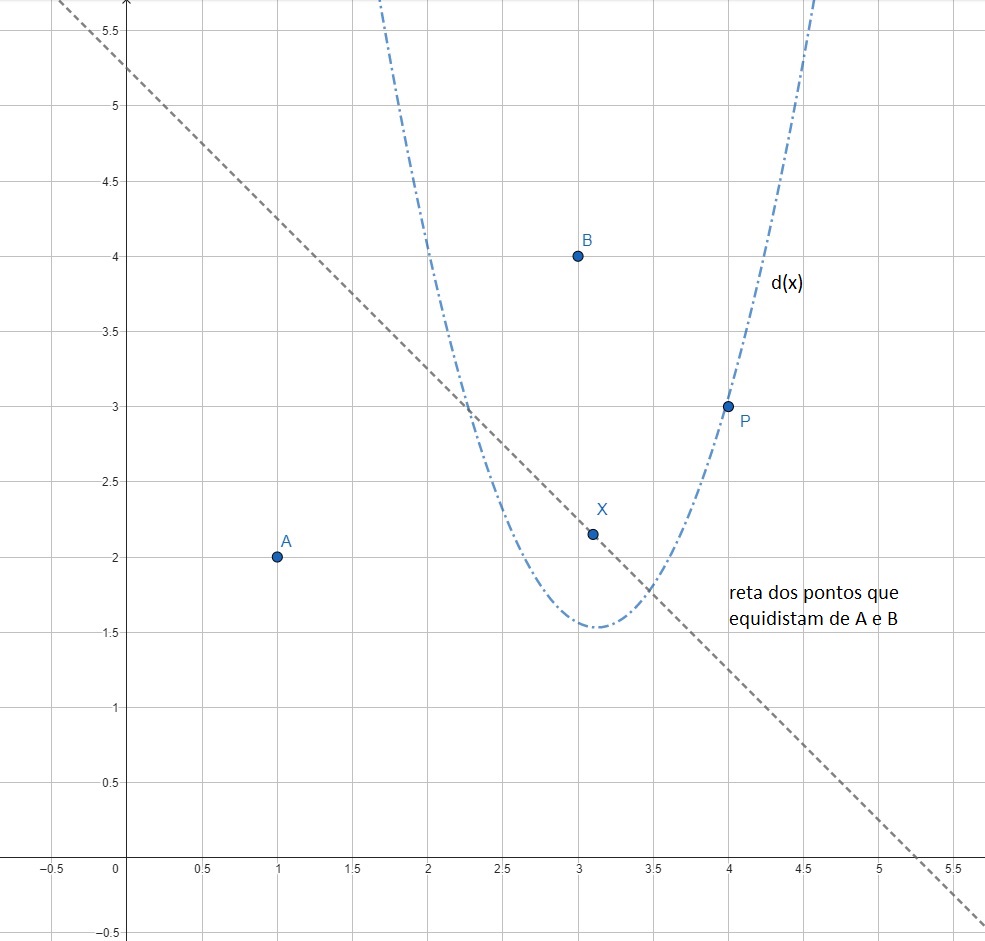
7) Mostre que os vetores da base ortonormal do \mathbb{R} ^2 , dados por \vec{i} = (1,0) e \vec{j} = (0,1) , são, de fato, unitários e ortogonais.

SOLUÇÃO: Primeiramente, observemos que os vetores são unitários:

• \left| \vec{i} \right| = \sqrt{1^2 + 0^2} = \sqrt{1} = 1 ;
• \left| \vec{j} \right| = \sqrt{0^2 + 1^2} = \sqrt{1} = 1 .

Agora, calculando o produto escalar, podemos ver que eles são, de fato, ortogonais: $$ \vec{i} \cdot \vec{j} = (1,0) \cdot (0,1) = 1 \times 0 +  0 \times 1 = 0.$$

8) Calcule a área do quadrilátero ABCD da figura abaixo:

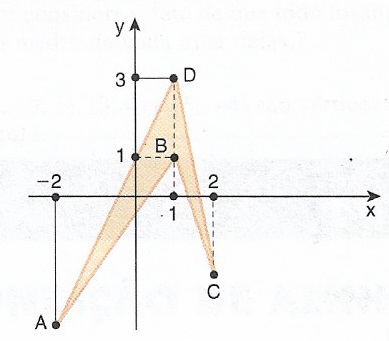
SOLUÇÃO: A área do quadrilátero hachurado é dada pela soma $$A = \text{Área do triângulo ABD} + \text{Área do triângulo BCD}$$ Observe que se considerarmos para o triângulo ABD a base BD antão a altura será a distância entre os pontos -2 e 1 sobre o eixo Ox. Logo $$ \text{Área do triângulo ABD} = \frac{BD \times h}{2} = \frac{(3-1) \times |1 – (-2) |}{2} = 3.$$ Analogamente,  se considerarmos para o triângulo BCD a base BD antão a altura será a distância entre os pontos 1 e 2 sobre o eixo Ox . Logo, $$ \text{Área do triângulo BCD} = \frac{BD \times h}{2} = \frac{(3-1) \times |2 – 1 |}{2} = 1.$$ Portanto, $$\text{Área do quadrilátero ABCD} = \text{Área do triângulo ABD} + \text{Área do triângulo BCD} = 4.$$

9) Sejam dados os pontos A(1,1) , B(2,3) , C(-4,1) e D(-2,1) . Determine a projeção ortogonal do vetor \vec{CD} sobre o vetor \vec{AB} .

SOLUÇÃO: O vetor \vec{AB} é dado por \vec{AB} = (2,3) - (1,1) = (1,2)  e o vetor \vec{CD} é dado por \vec{CD} = (-2,1) - (-4,1) = (2,0)  . Assim, a projeção ortogonal do vetor \vec{CD} sobre o vetor \vec{AB} é dado por $$ \text{proj}_{\vec{CD}} \vec{AB} =  \left( \frac{\vec{AB} \cdot \vec{CD}}{| \vec{AB} | ^2} \right) \vec{AB} = \left( \frac{(1,2) \cdot (2,0)}{| (1,2) | ^2} \right) (1,2)=\frac{2}{\sqrt{5}}(1,2)=\left( \frac{2 \sqrt{5}}{5} , \frac{4 \sqrt{5}}{5}\right).$$

Leia Mais

• Vetores no Plano R²: Norma e Produto Escalar
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• O que é um Vetor? Um guia ilustrado dos vetores no espaço.
• O Espaço R²: Coordenadas no Plano Cartesiano