Uma lista com 10 exercícios resolvidos para você entender de vez como resolver sistemas lineares, usando a eliminação gaussiana (escalonamento) ou a Regra de Cramer.

Um sistema de equações lineares ou sistema linear é um conjunto formado por duas ou mais equações lineares. Um sistema linear pode ser representado na forma: $$ \left\{ \begin{array}{lll} a_{11} x_1 + a_{12} x_2 +…+a_{1n} x_n & = & b_1\\ a_{21} x_1 + a_{22} x_2 +…+a_{2n} x_n & = & b_2\\ \vdots \\ a_{m1} x_1 + a_{m2} x_2 +…+a_{mn} x_n & = & b_m\\ \end{array} \right. \qquad (1)$$ onde, cada um dos a_{ij}são os coeficientes, x_i são as incógnitas e b_i são os termos independentes. Uma sequencia de números (r_1,r_2,...,r_n), chamada é solução do sistema linear acima se satisfaz todas as equações do sistema ao mesmo tempo. Se m = n dizemos que o sistema linear é de ordem n .
O número de soluções de um sistema linear determina a sua classificação de duas maneiras com relação à sua consistência:
- Sistema possível ou consistente: Quando tem pelo menos uma solução. Se tem uma única solução, o sistema é determinado. Se tem mais que uma solução, o sistema é indeterminado.
- Sistema impossível ou inconsistente: Se não admite qualquer solução. Dois sistemas são equivalentes se admitem a mesma solução. Dois sistemas S_1 e S_2 equivalentes são denotados por S_1 \sim S_2.
$$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn}\\ \end{array} \right] $$ é a matriz dos coeficientes do sistema, $$ X = \left[ \begin{array}{cccc} x_1 \\ x_2 \\ \vdots \\ x_n\\ \end{array} \right] $$ é a matriz das incógnitas e $$ B = \left[ \begin{array}{cccc} b_{1} \\ b_{2} \\ \vdots \\ b_n\\ \end{array} \right] $$ é a matriz dos termos independentes. Portanto, uma forma de solucionar o sistema linear (1) é $$ X = \frac{1}{\text{det} (A) } \left[ \text{cof} (A) \right]^{T} \times B.$$
Desta fórmula também surge a regra de Cramer foi formada e desenvolvida pelo grande matemático Gabriel Cramer na década de 1750 . Ele usou o método de Cramer para encontrar a solução de um sistema de equações com [/katex] n [/katex] variáveis e o mesmo número de equações. Gabriel Cramer trabalhou em análise e determinantes. Ele é mais conhecido por sua fórmula para resolver equações simultâneas. Neste caso, $$x_k = \frac{\text{det} \left( \Delta _k \right) }{\text{det} \left( A \right)}, \qquad k = 1,2,3, \cdots, n .$$ Esta fórmula dá a solução do sistema $$ A \times X = B $$ quando \text{det} (A) \neq 0, ou seja, a matriz A é inversível, é conhecida como Regra de Cramer.
Lista de 10 Exercícios Resolvidos Sobre Sistemas Lineares
1) Resolva os sistemas lineares abaixo pela Regra de Cramer:
a) \left\{ \begin{array}{lll} 2x +3y & = & 8 \\ x - y & = & -1 \\ \end{array} \right. ;
SOLUÇÃO:
b) \left\{ \begin{array}{lll} 3x - y + z & = & 5 \\ x+3y & = & 7 \\ 2x + y - 2z & = & -4 \\ \end{array} \right. ;
SOLUÇÃO:
c) \left\{ \begin{array}{lll} 5x - 2y + 2z & = & 2 \\ 3x+y +4z & = & -1 \\ 4x -3 y + z & = & 3 \\ \end{array} \right. ;
SOLUÇÃO:
2) Discuta os sistemas lineares abaixo quanto a sua solução:
a) \left\{ \begin{array}{lll} x + y +2z & = & 1 \\ 2y-z & = & 2 \\ \end{array} \right. ;
SOLUÇÃO:
b) \left\{ \begin{array}{lll} x + 3y -z & = & 4 \\ 3y+z & = & 1 \\ \end{array} \right. ;
SOLUÇÃO:
c) \left\{ \begin{array}{lll} 2x + y + z & = & 5 \\ 3x-y-2z & = & -2 \\ x + 2y - z & = & 1 \\ \end{array} \right. ;
SOLUÇÃO: 
d) \left\{ \begin{array}{lll} 3x + y - z & = & 3 \\ 2x-y+3z & = & 5 \\ 8x + y + z & = & 11 \\ \end{array} \right. ;
SOLUÇÃO: 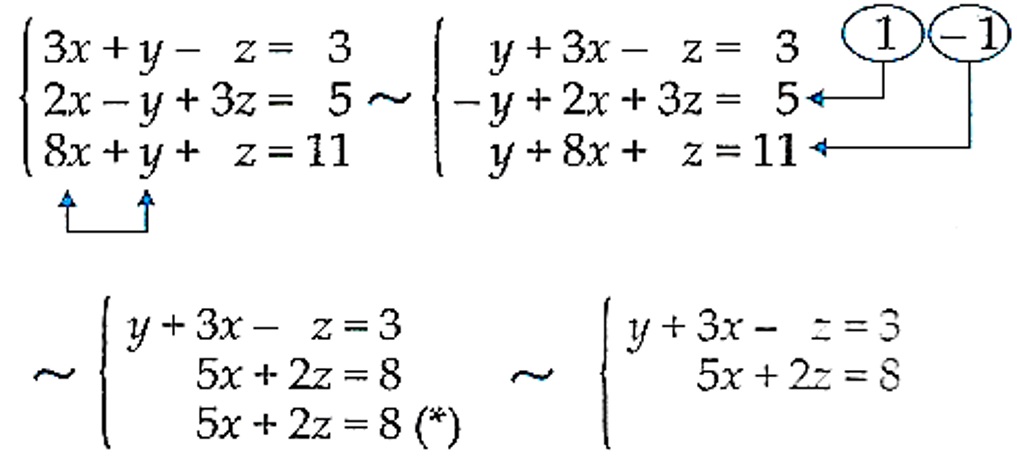
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
e) \left\{ \begin{array}{lll} 2x + 5y + z & = & 5 \\ x+2y-z & = & 3 \\ 4x + 9 y - z & = & 8 \\ \end{array} \right. ;
SOLUÇÃO: 
3) Resolver por Escalonamento o sistema \left\{ \begin{array}{lll} x + y + z & = & 2 \\ x-y-z & = & -3 \\ 2x + y + 2 z & = & 1 \\ 3x + 2y + 3 z & = & 3 \\ \end{array} \right. .
SOLUÇÃO:
4) Resolva o sistema: \left\{ \begin{array}{lll} x^2 + y^2 & = & 34 \\ -x^2 + y^2 & = & 16 \\ \end{array} \right. .
SOLUÇÃO:
| Livro referência deste artigo sobre a Eliminação Gaussiana (ou Escalonamento): “Álgebra linear e suas aplicações”, de Gilbert Strang. |
| Livro referência deste artigo sobre a Regra de Cramer: “Álgebra linear”, de Alfredo Steinbruch e Paulo Winterle. |
Leia Mais:
- Sistemas Lineares de Ordem 2: Métodos da Adição e da Substituição
- Sistemas Lineares mxn: Eliminação Gaussiana ou Escalonamento
- Sistemas Lineares: Forma Matricial e a Regra de Cramer
- Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió
- Inversão de Matrizes | Como calcular inversa de uma matriz?

