Retas no Plano: 7 Exercícios Resolvidos sobre Equações e Posições Relativas

Explore exercícios resolvidos que aprofundam seu entendimento sobre equações e posições relativas de retas no plano. Aprenda a abordar desafios matemáticos envolvendo a interseção e a disposição das retas, aprimorando suas habilidades analíticas.

Os elementos fundamentais na geometria plana são os pontos e as retas. O plano é composto por pontos, e as retas são conjuntos distintos desses pontos no plano. Pontos e retas obedecem a cinco conjuntos de axiomas que formam a base da geometria euclidiana plana.

Em essência, duas retas no plano devem ser necessariamente paralelas ou concorrentes. Assim, ao definirmos uma reta como paralela, automaticamente estamos estabelecendo que as retas são concorrentes. Consequentemente, a medida da distância entre duas retas no plano só é significativa se as retas forem paralelas. Caso contrário, se forem concorrentes, a distância é zero, uma vez que possuem um ponto de interseção.

Esta compilação de exercícios resolvidos é ideal para aqueles que desejam aprofundar sua compreensão sobre retas, incluindo equações e posições relativas, no plano cartesiano. Ao abordar esses problemas, você terá a oportunidade de aprimorar seu raciocínio lógico na área da geometria analítica, proporcionando uma abordagem prática para consolidar seus conhecimentos sobre esse aspecto específico da matemática.

7 Exercícios Resolvidos sobre Equações e Posições Relativas de Retas no Plano

1) Encontre as equações paramétricas e vetoriais para a reta no plano que passa pelo ponto P(2,3) na direção do vetor \vec{v} = (1, -2) .

Solução: Como a reta que temos passa pelo ponto P(2,3) na direção do vetor \vec{v} = (1, -2) , então, sua equação vetorial será $$ (x,y) = (2,3)+t (1,-2), \qquad t \in \mathbb{R}.$$ Daí, as equações paramétricas desta reta serão $$ r:\; \left\{ \begin{array}{lll} x  & = & 2 + t \\ & \\ y &= & 3-2t \\ \end{array} \right. ; \qquad t \in \mathbb{R} .$$

2) Encontre as equações paramétricas da reta que passem pelos pontos P(-1,-3) e Q(4,2) .

Solução: Se a reta passa pelos pontos P(-1,-3) e Q(4,2) , então o vetor $$ \vec{v} = \vec{PQ} = Q\; – \; P = (4,2) – (-1, -3) = (5,5)$$ é seu vetor diretor. Portanto, as equações paramétricas da reta que passa pelos pontos P e Q são dadas por $$ r:\; \left\{ \begin{array}{lll} x  & = & -1+5t \\ & \\ y &= & -3 +5t\\ \end{array} \right. ; \qquad t \in \mathbb{R} $$ se usarmos o ponto P . Da mesma maneira, se usarmos o ponto Q temos como equações paramétricas $$ r:\; \left\{ \begin{array}{lll} x  & = & 4+5 \lambda \\ & \\ y &= & 2 +5 \lambda \\ \end{array} \right. ; \qquad \lambda \in \mathbb{R}. $$ As duas formas de escrever as equações paramétricas determinam a mesma reta.

3) Encontre a reta s que é perpendicular à reta r de equação vetorial $$ r: (x,y) = (2,0) + t (0,1).$$

Solução: A reta  r está escrita em sua equação vetorial, logo, seu vetor diretor é dado por \vec{v} = (0,1) = \vec{j} , ou seja, esta reta é paralela ao eixo Oy. Logo, a reta perpendicular a r , é paralela ao eixo Ox e tem como vetor normal, o vetor \vec{u} , que é paralelo ao vetor diretor de   r . Assim, o vetor \vec{v} = (0,1) = \vec{j} é normal à reta s e,  portanto, sua equação geral é dada por $$ 0 \cdot x + 1 \cdot y + c = 0 \Leftrightarrow y = -c .$$ Logo, todas as retas na forma $$ s: y = -c, \qquad c \in \mathbb{R} $$ é perpendicular à reta r: (x,y) = (2,0) + t (0,1) .

4) Estude a posição relativa entre as retas r: 3x+y = 4 e s: x -y = 5 . Se elas forem concorrentes, encontre o ponto de interseção e o àngulo entre as retas. Se forem paralelas, determine a distância entre elas.

Solução: As duas equações estão escritas em sua forma geral, logo, os vetores $$ \vec{n}_{r} = (3,1) \qquad \text{e} \qquad \vec{n}_{s} = (1,-1) $$ são, respectivamente, os vetores normais a r e a s . Como $$ \frac{3}{1} \neq \frac{1}{-1} $$ então estes vetores normais não são paralelos e, assim, as retas também não são paralelas. Desta forma, existe um ponto de interseção entre estas duas retas que será a solução do sistema linear dado por $$ \left\{ \begin{array}{lll} 3x+y & = & 4 \\ & \\ x-y &= & 5 \\ \end{array} \right.$$ donde encontramos $$4x = 9 \Rightarrow x = \frac{9}{4} \Rightarrow \frac{9}{4} – y = 5 \Rightarrow y = \frac{9}{4} – 5 = – \frac{11}{4}.$$ Portanto, o ponto de interseção entre as retas r e s é A \left( \dfrac{9}{4} , - \dfrac{11}{4} \right)  . Já o ângulo \theta entre as duas retas será dado pelo ângulo entre os vetores \vec{n}_{r} e \vec{n}_{s} : $$ \text{cos}( \theta ) =  \frac{| \vec{n}_{r} \cdot \vec{n}_{s} |}{\| \vec{n}_{r} \| \| \vec{n}_{s}\|} = \frac{| 3-1|}{\sqrt{10} \sqrt{2} } = \frac{2}{2 \sqrt{5}} = \frac{\sqrt{5}}{5}.$$ Portanto, o ângulo \theta entre as retas r e s é $$ \theta = \text{arc cos}\left( \frac{\sqrt{5}}{5} \right) \approx 63º = \frac{7}{20} \pi \text{rad}.$$

5) Num triângulo ABC , A(1,-2) , B(2,3) , C pertence à reta r: 2x+y-2 = 0 e a área é igual a 8. Determine o ponto C .

Solução: Como o ponto C pertence à reta r: 2x+y-2 = 0 , então, observando que 2x+y-2 = 0 \Rightarrow y = -2x +2 , obtemos $$ C (x, -2x +2).$$ Isso está ilustrado na figura abaixo:

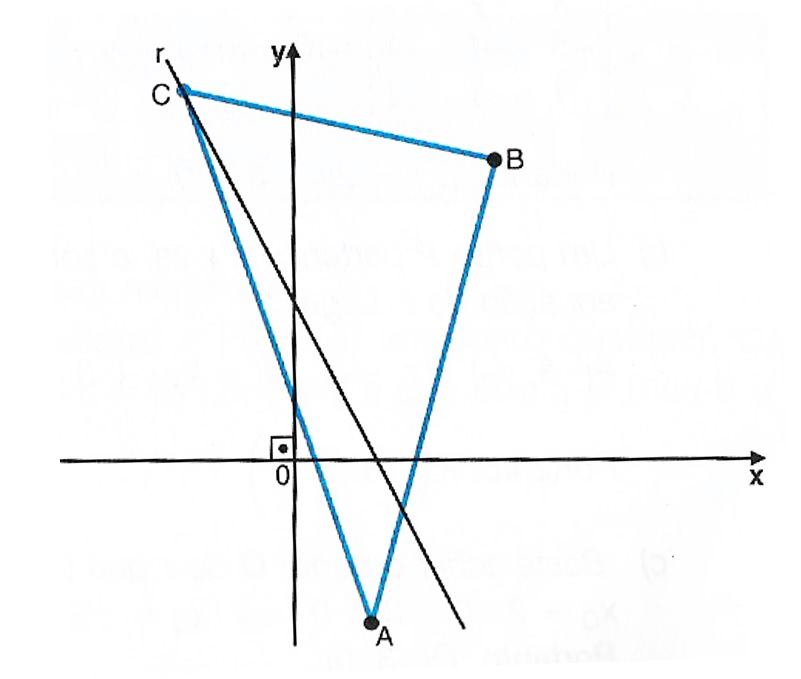
Agora, como a área do triângulo ABC é igual a 8, então $$| 8 | = \frac{1}{2} \left| \begin{array}{ccc} 1 & -2 & 1 \\ 2 & 3 & 1 \\ x & -2x +2 & 1 \end{array} \right| \Rightarrow  | 16 | =  \left| \begin{array}{ccc}1 & -2 & 1 \\ 2 & 3 & 1 \\ x & -2x +2 & 1 \end{array} \right|$$ Assim, $$ 9 \; – \; 7x = \pm 16 $$ o que nos leva a $$ -7x + 9 =  16  \Leftrightarrow x = -1 $$ e $$ -7x + 9 =  – 16  \Leftrightarrow x = – \frac{25}{7} $$Portanto, a coordenada x é igual a -1 ou - \dfrac{25}{7} . Substituindo nas coordenadas C (x, -2x +2) , obtemos, enfim, $$ C (-1, 4) \qquad \text{ou} \qquad C \left( \frac{25}{7}, -\frac{36}{7} \right) .$$

Abaixo temos uma ilustração destes dois pontos que encontramos:

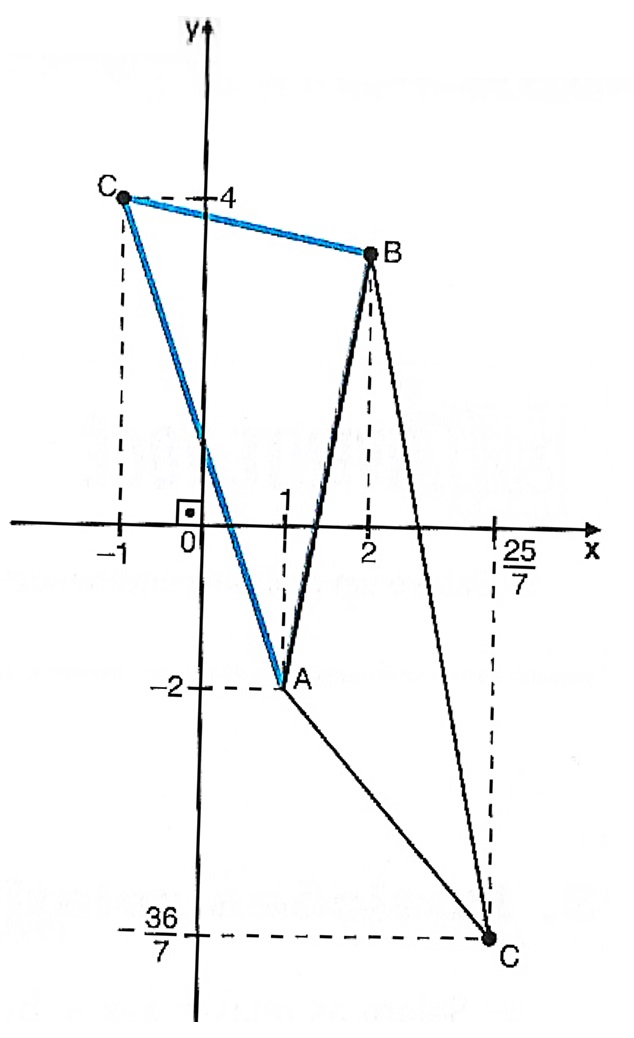
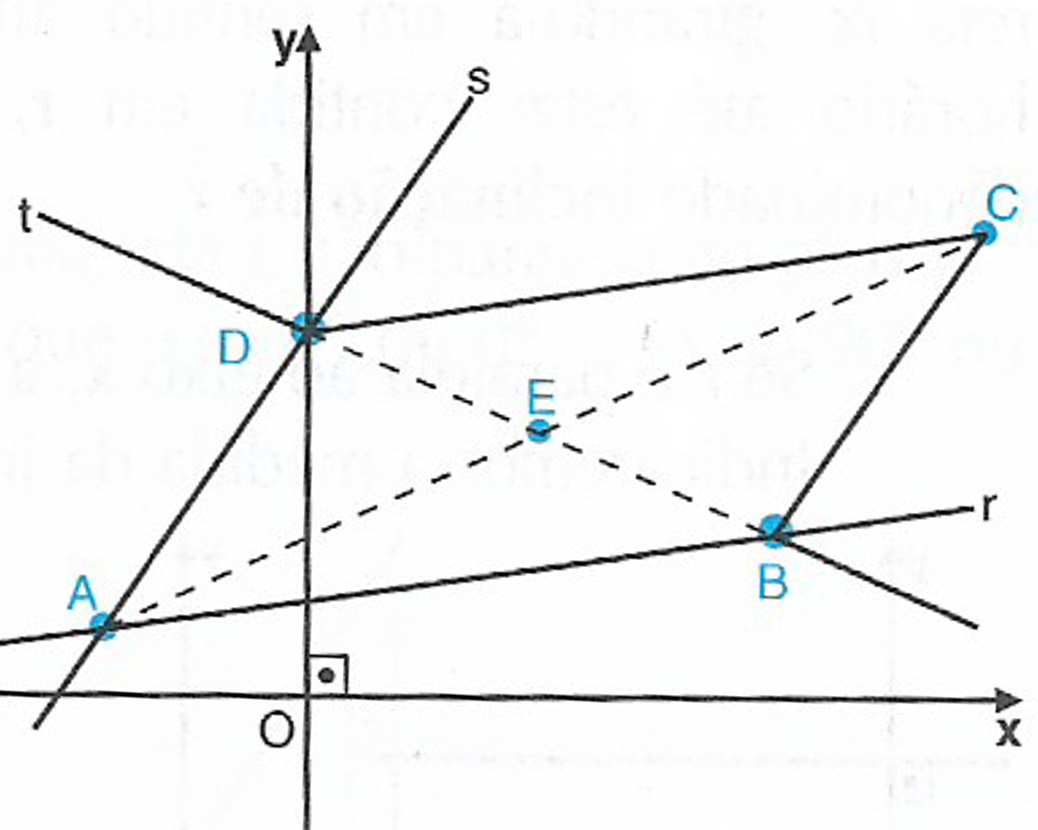
6) Dois lados de um paralelogramo estão contidos nas retas r: x-6y+8  = 0 e s: 3x-2y+8 = 0 e uma das diagonais está contida na reta t: x+2y-8 = 0. Quais são os vértices desse paralelogramo.

Solução: Um dos vértices é o ponto de intersecção de r e de s ; resolvendo o sistema: $$ \left\{ \begin{array}{lll}x-6y+8 & = &0 \\ & \\ 3x -2y+8 &= & 0 \\ \end{array} \right.$$ obtemos x = -2 e y = 1 . Logo, um dos vértices é A(-2,1).

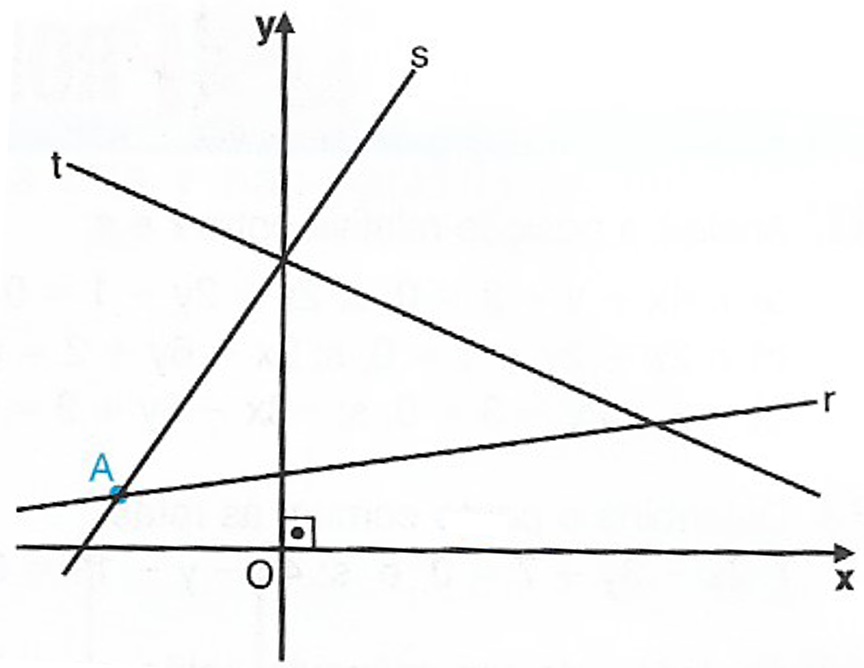
Note que A \notin t , pois -2+2 \cdot 1-8 \neq 0 . Observe que se A pertencesse a t , não seria possível determinar os vértices do paralelogramo e haveria infinitas soluções para o problema. Então a interseção de t com r e a interseção de t com s são dois outros vértices do paralelogramo. Resolvendo $$ \left\{ \begin{array}{lll}x + 2y -8 & = &0 \\ & \\ x – 6y +8 &= & 0 \\ \end{array} \right.$$ obtemos x = 4 e y = 2 . Agora, resolvendo $$ \left\{ \begin{array}{lll}x + 2y -8 & = &0 \\ & \\ 3x – 2y +8 &= & 0 \\ \end{array} \right.$$ obtemos x = 0 e y = 4 . Logo, teremos os vértices B(4,2) e D(0,4).

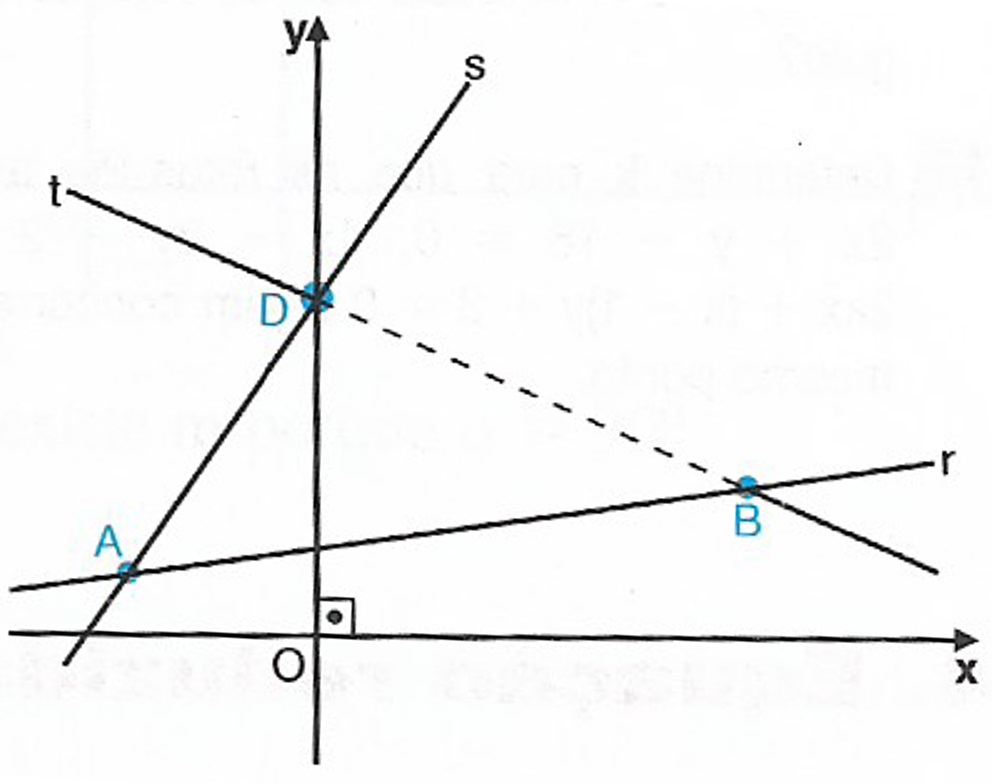
Sendo E o ponto médio do segmento BD , temos que E(2,3) usando a fórmula do ponto médio. Por propriedade do paralelogramo temos que E é o ponto médio também da outra diagonal, AC , então $$ \frac{x_{A} + x_{C} }{2} = x_{E} \Rightarrow  \frac{-2 + x_{C} }{2} = 2 \Rightarrow x_{C} = 6 $$ $$ \frac{y_{A} + y_{C} }{2} = y_{E} \Rightarrow  \frac{1 + y_{C} }{2} = 3 \Rightarrow y_{C} = 5 $$ Portanto, C(6,5) .

7) Obtenha uma equação da reta s que passa por P(3,5) e forma ângulo de \pi / 4 com r: x - 2 y -4 = 0 .

Solução: A reta s tem equação y - y_{P} = m_{s} \left( x - x_{P} \right) e r e s   formam um ângulo agudo \beta = \frac{ \pi }{4} ; e pela equação da reta r temos que m_{r} = \dfrac{1}{2}. Para calcular m_{s} , temos: $$ \text{tg} \beta = \left| \frac{m_r – m_s}{1 + m_r m_s} \right| \Rightarrow \text{tg} \frac{\pi}{4} = \left| \frac{\frac{1}{2} – m_s}{1 + \frac{1}{2} m_s} \right| \Rightarrow 1 = \left| \frac{1 – 2m_s}{2 + m_s} \right| \Rightarrow \frac{1 – 2m_s}{2 + m_s} = \pm 1 $$ O que nos leva a $$ \frac{1 – 2m_s}{2 + m_s} = 1 \Rightarrow m_s = – \frac{1}{3} $$ ou $$ \frac{1 – 2m_s}{2 + m_s} = -1 \Rightarrow m_s = 3 .$$ Em y - y_{P} = m_{s} \left( x - x_{P} \right) , sabendo que s passa por P(3,5) , vem:

1. Se m_s = - \dfrac{1}{3} temos a equação geral de s dada por $$ x + 3y -18 = 0 ;$$
2. Se m_s = 3 temos a equação geral de s dada por $$ 3x – y – 4 = 0 .$$

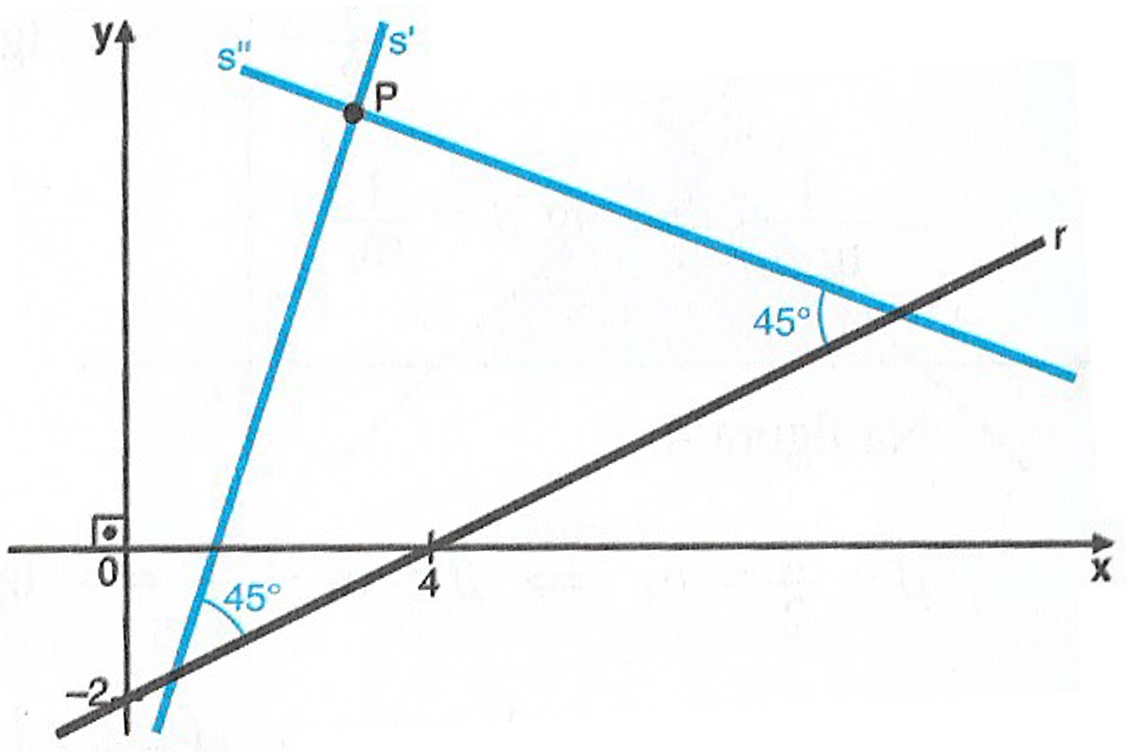
Logo, a reta que passa por P(3,5) e forma um ângulo de \pi / 4 com r tem equação dada por x + 3y -18 = 0 ou 3x - y - 4 = 0 . Abaixo, temos uma representação do porque temos estas duas possibilidades.

Leia Mais:

• Retas no Plano Cartesiano: Equações Reduzida, Geral, Vetorial e Paramétrica
• Retas No Plano Cartesiano: Posições Relativas Entre Retas
• Retas no Plano Cartesiano: 1ª Lista de Exercícios Resolvidos
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• Vetores no Plano R²: Norma e Produto Escalar