Vetores no R³: O Produto Vetorial e suas Interpretações Geométricas

O produto vetorial é uma operação binária entre dois vetores tridimensionais que produz um terceiro vetor que é ortogonal ao plano formado pelos vetores de entrada.

A Geometria Analítica é uma das disciplinas matemáticas fundamentais que desempenha um papel essencial em várias áreas da ciência e engenharia. No cerne dessa disciplina, encontramos operações que descrevem as relações entre vetores. Entre essas operações, o “produto vetorial” se destaca como uma ferramenta poderosa para compreender e resolver problemas geométricos, físicos e computacionais em três dimensões.

O produto vetorial é uma operação binária entre dois vetores tridimensionais que produz um terceiro vetor que é ortogonal ao plano formado pelos vetores de entrada. Esse conceito é de suma importância na geometria tridimensional e é amplamente aplicado em áreas como física, engenharia e computação gráfica. Ao compreender as propriedades fundamentais e as aplicações do produto vetorial, é possível desbloquear um conjunto diversificado de ferramentas matemáticas que tornam possível descrever e analisar fenômenos complexos do mundo real.

O Espaço  \mathbb{R}^3

O \mathbb{R} ^3 é o produto cartesiano   \mathbb{R} \times \mathbb{R} \times \mathbb{R} e pode ser representado pelo conjunto $$ \{ (x,y,z); x,y,z \in \mathbb{R} \}$$ e sua representação geométrica é o espaço cartesiano determinando pelos três eixos cartesianos dois a dois ortogonais Ox, Oy \text{ e } Oz .

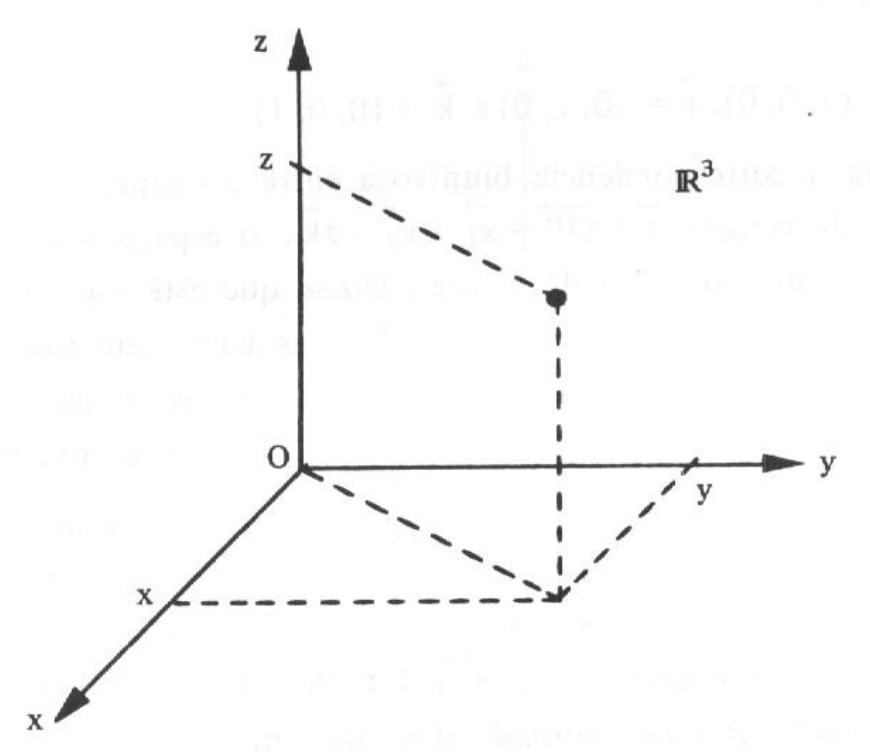
A cada ponto P do espaço vai corresponder uma terna (a,b,c) de números reais chamadas coordenadas de P e denominada abscissa, ordernada e cota, respectivamente. Cada uma destas coordenadas é obtida traçando planos paralelos aos planos coordenados,

A distância entre dois pontos do espaço \mathbb{R}^3, P(x_1 ,y_1 ,z_1) e Q(x_2 ,y_2 ,z_2) é dada por $$ d(x,y)  = \sqrt{(x_1-x_2)^2 +(y_1-y_2)^2+ (z_1-z_2)^2 } .$$ Como consequência desta definição podemos garantir que:

• A distância entre dois pontos distintos no \mathbb{R}^3 é sempre maior que zero;
• A distância entre dois pontos no \mathbb{R}^3 será nula se, e somente se, os dois pontos forem iguais;
• d(P,Q) = d(Q,P) ;
• d(P,Q) \leq d(P,R) + d(R,Q) ;

consideremos um vetor \vec{v} = x \vec{i} + y \vec{j} + z \vec{k} , onde os números reais a,b e c são números reais denominados componentes do vetor \vec{v} , na base canônica \{ \vec{i} , \vec{j} , \vec{k} \} .Analogamente como desenvolvemos no plano, este vetor \vec{v} é igual ao vetor \vec{OP} com O(0,0,0) e P(x,y,z) .

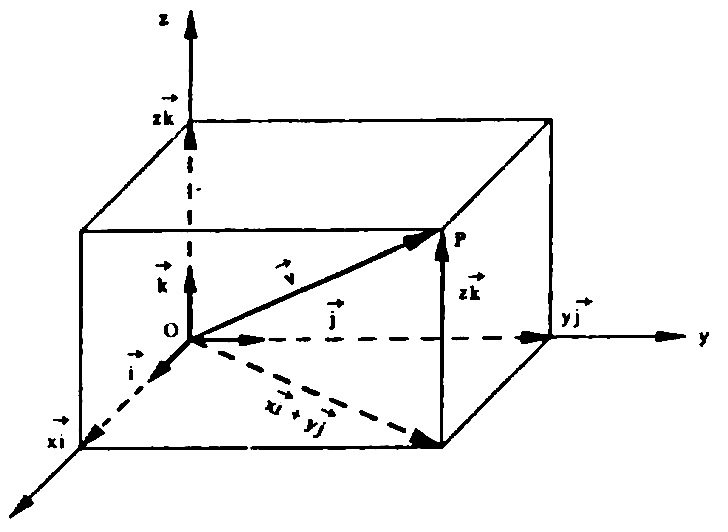
Este vetor, geometricamente, como vemos na figura anterior, irá corresponder à diagonal do paralellepípedom cujos lados são determinados pelos vetores x \vec{i} , y \vec{j} \text{ e } z \vec{k} . Para simplificar escrevemos $$ \vec{v} = (x,y,z)$$ que é a expressão analítica do vetor \vec{v} . Em particular $$ \vec{i} = (1,0,0); \\ \vec{j} = (0,1,0); \\ \vec{k} = (0,0,1) .$$

A reta com a direção do vetor \vec{i} é o eixo dos x (das abscissas), a reta com a direção do vetor \vec{j} é o eixo dos y (das ordenadas) e a reta com a direção do vetor \vec{k} é o eixo dos z (das cotas). As setas indicam o sentido de cada eixo.

O Produto Vetorial dentre Vetores no Espaço Tridimensional

Ao contrário do produto escalar, que dá como resultado um número e tem sentido tano no plano como no espaço, o produto vetorial é um modo de combinar vetores do espaço dando como resultado um outro vetor. Essa operação tem um significado geométrico interessante mas será definida algebricamente, a fim de facilitar a dedução de suas propriedades formais.

Chama-se produto vetorial de dois vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} + z_1 \vec{k} \qquad \text{e} \qquad \vec{v} = x_2 \vec{i} + y_2 \vec{j} + z_2 \vec{k} $$, tomado nesta ordem, se representa por \vec{u} \wedge \vec{v} (e lê-se “ \vec{u} vetorial \vec{v} “), ao vetor: $$ \vec{u} \wedge \vec{v} = (y_1 z_2 – z_1 y_2) \vec{i} – (x_1 z_2 – z_1x_2) \vec{j} + (x_1 y_2 – y_1 x_2) \vec{k}$$

Cada componente deste vetor pode ainda ser expresso na forma de uma determinante de 2ª ordem: $$ \vec{u} \wedge \vec{v} = \left| \begin{array}{cc} y_1 &  z_1 \\ y_2 & z_2 \end{array} \right| \vec{i} – \left| \begin{array}{cc} x_1 &  z_1 \\ x_2 & z_2 \end{array} \right| \vec{j}+ \left| \begin{array}{cc} x_1 &  y_1 \\ x_2 & y_2 \end{array} \right| \vec{k}$$

Partindo daí e usando o Teorema de Laplace podemos encontrar a fórmula para o produto vetorial como o determinante simbólico $$ \vec{u} \wedge \vec{v} = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ x_1 & y_1 &  z_1 \\ x_2 & y_2 & z_2 \end{array} \right| $$ onde \vec{i} =(1,0,0), \vec{j}=(0,1,0) e \vec{k}=(0,0,1)

Observações Importantes:

1. Se \theta é o ângulo entre os vetores \vec{u} e \vec{v}, então \left| \vec{u} \wedge \vec{v} \right| = \left| \vec{u} \right| \left|\vec{v}\right| \text{sen}(\theta);
2. O produto vetorial \vec{u} \wedge \vec{v} é perpendicular a \vec{u} e a \vec{v} simultaneamente.
3. Os vetores  \vec{u} \wedge \vec{v} e \vec{v} \wedge \vec{u} são opostos, isto é,  \vec{u} \wedge \vec{v} = - \vec{v} \wedge \vec{u} , o que significa que o produto vetorial não é comutativo.

EXEMPLO: Calcule o produto vetorial entre os vetores \vec{u} = (1,2,-1) e \vec{v} = (2,1,3): $$\left| \begin{array}{lcr} \vec{i}  & \vec{j} & \vec{k} \\ 1 & 2 & -1\\ 2 & 1 & 3 \end{array} \right|=7\vec{i}-5\vec{j}-3\vec{k}=(7, -5, -3)$$

Propriedades do Produto Vetorial

1. \vec{u} \wedge \vec{u} = \vec{0}, para todo vetor \vec{u} ;
2. \vec{u} \wedge \vec{v} = - \vec{v} \wedge \vec{u} ;
3. \vec{u} \wedge ( \vec{v} + \vec{w} ) = \vec{u} \wedge \vec{v} + \vec{u} \wedge \vec{w} ;
4. (m \vec{u}) \wedge \vec{v} = m ( \vec{u} \wedge \vec{v} ) ;
5. \vec{u} \wedge \vec{v} = 0 se, e somente se, um dos vetores é nulo, ou se \vec{u} e  \vec{v} são colineares;
6. \vec{u} \wedge \vec{v} é perpendicular a \vec{u} e a \vec{v} simultaneamente;
7. Os vetores \vec{u} e \vec{v} e \vec{u} \wedge \vec{v} têm as direções das arestas de um triedro.
8. O produto vetorial não é associativo.

Interpretação Geométrica do Módulo do produto Vetorial de Dois Vetores

Geometricamente, o módulo do produto vetorial dos vetores \vec{u} e \vec{v} mede a área do paralelogramo ABCD determinado pelos vetores \vec{u} = \vec{AB} e \vec{v} = \vec{AC} , como ilustrado na figura abaixo:

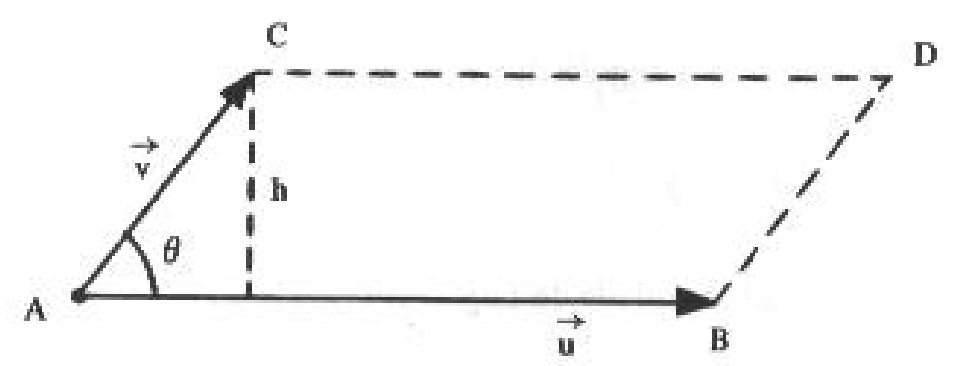
De fato: Da geometria clássica, sabemos que $$ \text{ Área ABCD} = | \vec{u} | h,$$ mas como $$ h = | \vec{v} | \text{sen}( \theta ) $$ então $$ \text{ Área ABCD} = | \vec{u} | | \vec{v} | \text{sen}( \theta ).$$ Logo, como \left| \vec{u} \wedge \vec{v} \right| = \left| \vec{u} \right| \left|\vec{v}\right| \text{sen}(\theta), concluímos que $$ \text{ Área ABCD} = \left| \vec{u} \wedge \vec{v} \right| .$$

Observação: Obviamente, a área do triângulo ABC determinado pelos vetores \vec{u} = \vec{AB} e \vec{v} = \vec{AC} é metade da área do paralelogramo, logo $$ \text{ Área ABC} = \frac{\left| \vec{u} \wedge \vec{v} \right|}{2}.$$

Exemplos:

1) Determinar um vetor unitário simultaneamente ortogonal aos vetores \vec{u} = (2,-6,3) e \vec{v} = (4,3,1). 

Solução: Como o produto vetorial \vec{u} \wedge \vec{v} é ortogonal a \vec{u} e a \vec{v} simultaneamente, então, $$ \vec{w} = \vec{u} \wedge \vec{v} = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 2 & -6 &  3 \\ 4 & 3 & 1 \end{array} \right| = (-6 -9) \vec{i} – (2 -12) \vec{j} + (6 + 24) \vec{k} = (-15,10,30). $$ Obviamente, o vetor - \vec{w} = (15,-10,-30) também é ortogonal aos dois vetores simultaneamente. Como ambos possuem a mesma norma dada por 35, então, os vetores $$ \frac{\vec{w}}{| \vec{w} |} =  \left( -\frac{3}{7} , \frac{2}{7} , \frac{6}{7} \right) \qquad \text{e} \qquad \frac{-\vec{w}}{| \vec{w} |} =  \left( \frac{3}{7} , -\frac{2}{7} , -\frac{6}{7} \right).$$

2) Dados os vetores \vec{u} = (1,2,-1) e \vec{v} = (0,-1,3), calcular a área do paralelogramo determinado pelos vetores 3 \vec{u} e \vec{v} - \vec{u} .

Solução: Primeiramente, note que $$ 3 \vec{u} = (3,6,-1) $$ $$ \vec{v} – \vec{u} = (-1, -3 , 4 ).$$ Agora, podemos determinar a área do paralelogramo como $$ A = | 3 \vec{u} \wedge (\vec{v} – \vec{u}) | = \text{a norma do vetor} \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 3 & 6 &  -1 \\ 0 & -1 & 3 \end{array} \right| = | (15,-9,-3)| = 3 \sqrt{35}.$$ Portanto, A área deste paralelogramo é dada por 3 \sqrt{35} unidades de área.

3) Calcular a área do triângulo de vértices A (1,-2,1) , B (2,-1,4) e C (-1,-3,3) . 

Solução: Considerando o paralelogramo determinado pelos vetores \vec{AB} = (1, 1, 3) e \vec{AC} = (-2, -1, 2) , temos que $$ \text{ Área ABC} = \frac{| \vec{AB} \wedge \vec{AC} |}{2} = \frac{| (1, 1, 3) \wedge (-2, -1, 2) |}{2}.$$ Como $$ \vec{AB} \wedge \vec{AC} =  \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 1 & 1 & 3 \\ -2 & -1 & 2 \end{array} \right| = (5,-8,1)$$ então $$ | \vec{AB} \wedge \vec{AC} | = |(5,-8,1)| = 3 \sqrt{10}.$$ Portanto $$ \text{ Área ABC} = \frac{| \vec{AB} \wedge \vec{AC} |}{2} = \frac{3 \sqrt{10}}{2} \text{u. a.}$$

Leia Mais:

• Vetores no R³: O Produto Escalar e suas Interpretações Geométricas
• Vetores No R³: Um guia ilustrado dos vetores no espaço euclidiano
• Vetores no Plano R²: Norma e Produto Escalar
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano