PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Você está tendo dificuldade para entender a lógica dos vetores no espaço tridimensional? Este guia ilustrado detalha tudo o que você precisa saber sobre matemática vetorial em três dimensões.

No mundo da matemática e da física, os vetores desempenham um papel fundamental na representação e análise de fenômenos tridimensionais. O espaço tridimensional, representado por \mathbb{R} ^3 , é um ambiente rico e complexo que oferece um vasto campo de estudo para os vetores. Este artigo é uma exploração aprofundada da teoria e aplicação de vetores em \mathbb{R} ^3 , abrangendo conceitos essenciais como decomposição, base canônica, soma e multiplicação por escalar.
Este artigo representa uma exploração abrangente dos vetores no espaço tridimensional \mathbb{R} ^3 , cobrindo tópicos essenciais como decomposição, base canônica, soma e suas aplicações em diversas disciplinas. A compreensão desses conceitos é fundamental para resolver problemas complexos e modelar fenômenos tridimensionais, tornando os vetores em \mathbb{R} ^3 uma ferramenta valiosa em matemática, física, engenharia e muito mais. Através deste estudo, esperamos que os leitores adquiram um conhecimento sólido que possa ser aplicado em uma ampla variedade de situações do mundo real.
Introdução às noções geométricas dos vetores
Neste artigo, vamos mostrar uma forma de representar os segmentos orientados relacionados com os sistemas de eixos cartesianos no plano. Geometricamente, um vetor determinado por um segmento orientado AB é o conjunto de todos os segmentos orientados equipolentes a AB , como representado na figura abaixo.
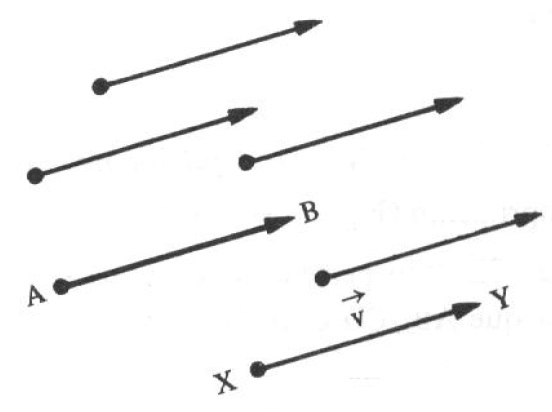
Se indicarmos como \vec{v} este conjunto, simbolicamente poderemos escrever: $$ \vec{v} = \left\{ XY; XY \sim AB \right\}$$ onde XY é um segmento qualquer do conjunto. O vetor determinado por AB é indicado por \vec{AB} ou B - A ou \vec{v} .
Portanto, um mesmo vetor \vec{AB} é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, e todos equipolentes entre si. Ou seja, todos com mesma direção, sentido e comprimento. O módulo de \vec{v} se indica por | \vec{v} | .
OBSERVAÇÃO:
- Dois vetores \vec{u} e \vec{v} são colineares se tiverem a mesma direção, ou seja, se tiverem representantes pertencentes a uma mesma reta ou a retas paralelas.

Vetores Colineares - Se os vetores não nulos \vec{u} , \vec{v} e \vec{w} possuem representantes pertencentes a um mesmo plano são ditos complanares. Dois vetores são sempre coplanares, mas três vetores poderão ou não ser coplanares.

Vetores coplanares e não-coplanares
| Os livros usados como referência deste artigo sobre Vetores no Plano são dados abaixo: | ||
O \mathbb{R} ^3 como um Espaço Vetorial
No espaço \mathbb{R} ^3 , qualquer conjunto \{ \vec{v_1} , \vec{v_2} , \vec{v_3} \} de três vetores não coplanares é uma base deste espaço e, de forma análoga, demonstra-se que todo vetor \vec{v} do espaço é combinação linear dos vetores da base, isto é, sempre existem números reais a_1 , a_2 e a_3 , tais que $$ \vec{v} = a_1 \vec{v_1} + a_2 \vec{v_2} + a_3 \vec{v_3} $$ onde a_1 , a_2 e a_3 são as componentes de \vec{v} em relação à base considerada.
A Base Ortonormal do Espaço \mathbb{R} ^3
Uma base no espaço é ortonormal se os três vetores forem unitários e dois a dois, ortogonais. Por analogia ao que fizemos no plano, neste artigo, das infinitas bases ortonormais existentes, escolheremos para nosso estudo a base canônica representada por \{ \vec{i} , \vec{j} , \vec{k} \} , todos considerados na origem do sistema tridimensional como mostrado na imagem abaixo.
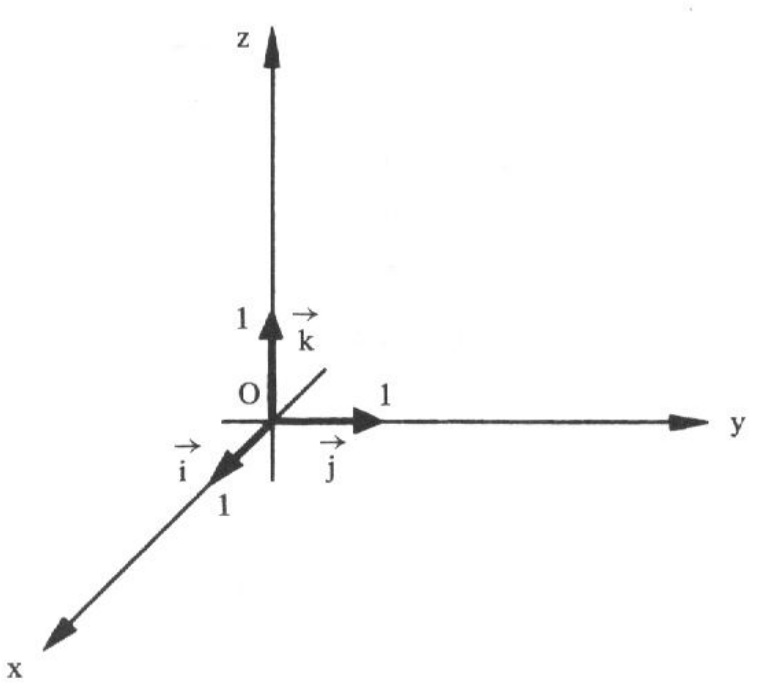
A reta com a direção do vetor \vec{i} é o eixo dos x (das abscissas), a reta com a direção do vetor \vec{j} é o eixo dos y (das ordenadas) e a reta com a direção do vetor \vec{k} é o eixo dos z (das cotas). As setas indicam o sentido de cada eixo.
Cada dupla de eixos determina um plano coordenado. Portanto, temos três planos coordenados: o plano xOy , o plano xOz e o plano yOz , que são representados na figura abaixo:
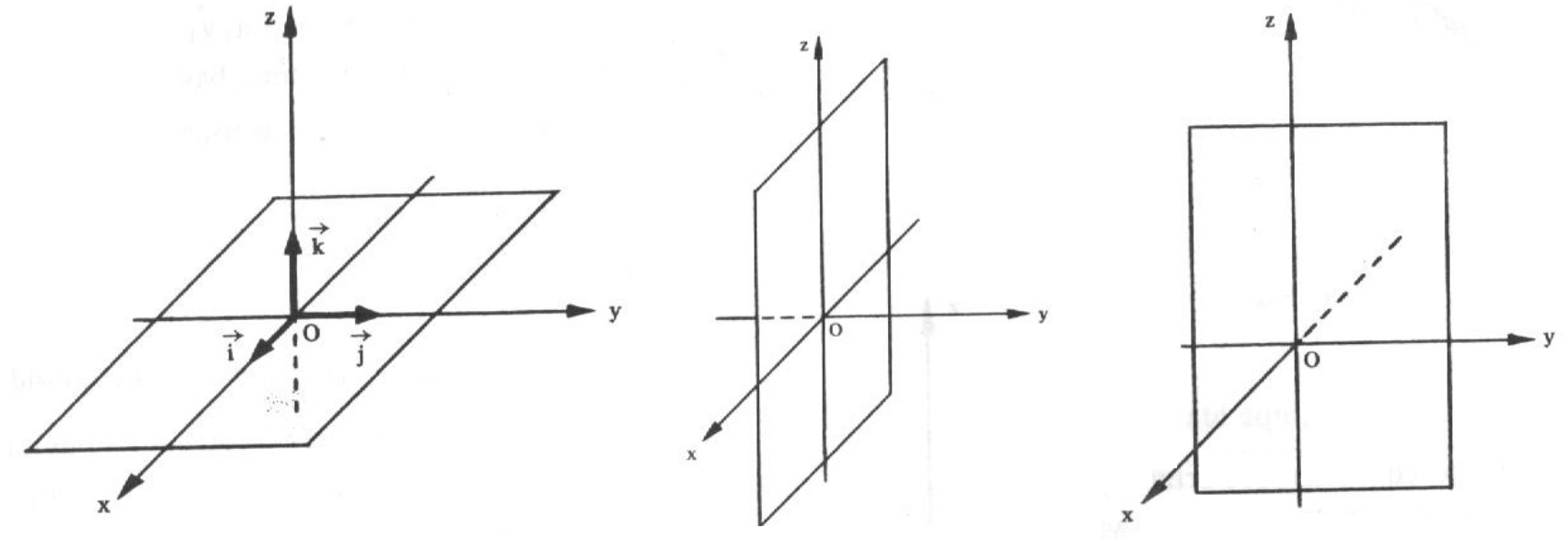
Estes três planos se interceptam segundo os três eixos dividindo o espaço em oito regiões, cada uma delas chamada octante. as figuras abaixo dão uma ideia gráfica do primeiro, segundo e terceiro octantes:
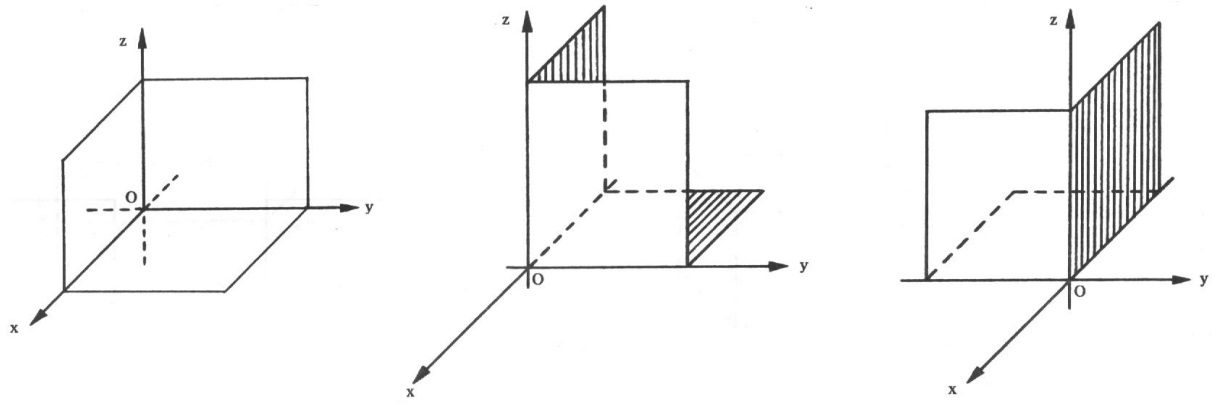
A cada ponto P do espaço vai corresponder uma terna (a,b,c) de números reais chamadas coordenadas de P e denominada abscissa, ordernada e cota, respectivamente. Cada uma destas coordenadas é obtida traçando planos paralelos aos planos coordenados, como ilustrado abaixo:
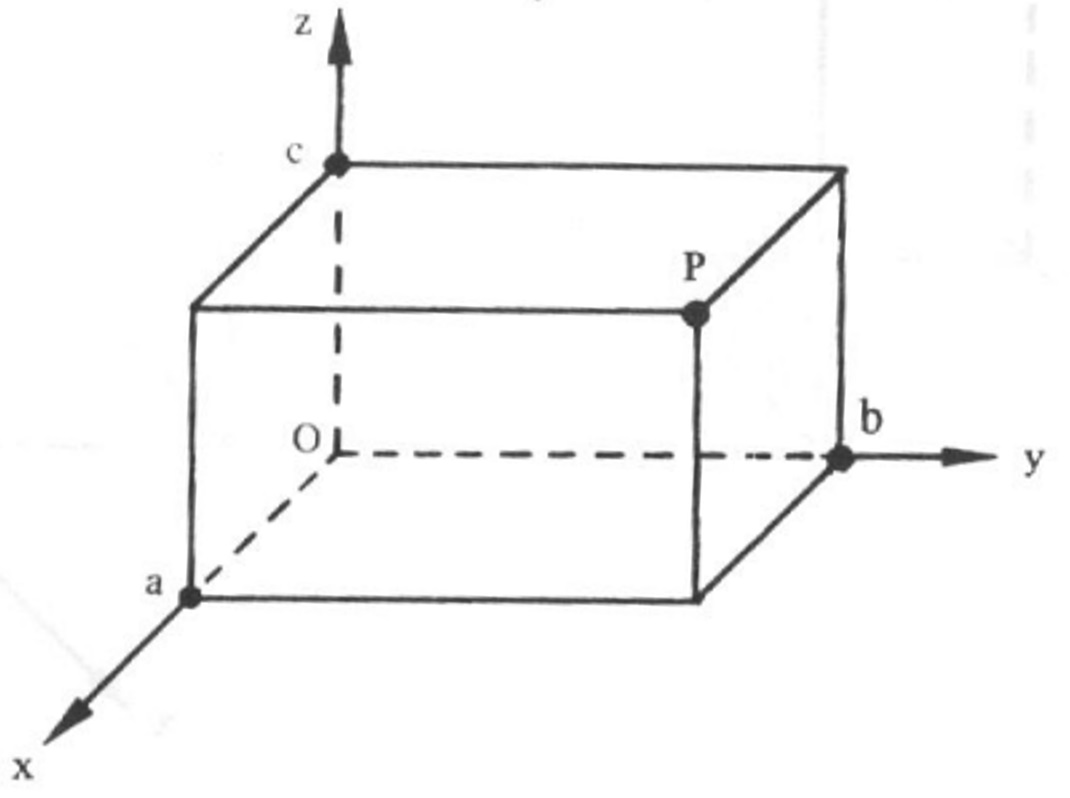
Com este procedimento de traçar três planos pelo ponto P , fica determinando um paralelepípedo retângulo.
A Decomposição Vetorial no \mathbb{R} ^3
Para completar nosso estudo, consideremos um vetor \vec{v} = x \vec{i} + y \vec{j} + z \vec{k} , onde os números reais a,b e c são números reais denominados componentes do vetor \vec{v} , na base canônica \{ \vec{i} , \vec{j} , \vec{k} \} .Analogamente como desenvolvemos no plano, este vetor \vec{v} é igual ao vetor \vec{OP} com O(0,0,0) e P(x,y,z) .
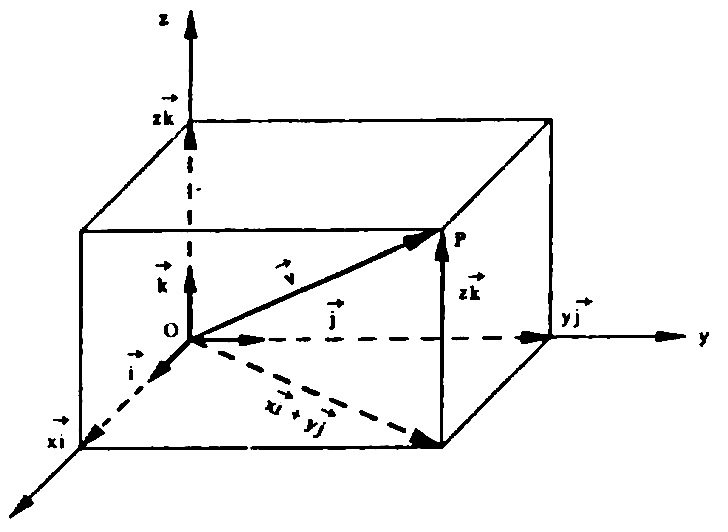
Este vetor, geometricamente, como vemos na figura anterior, irá corresponder à diagonal do paralellepípedom cujos lados são determinados pelos vetores x \vec{i} , y \vec{j} \text{ e } z \vec{k} . Para simplificar escrevemos $$ \vec{v} = (x,y,z)$$ que é a expressão analítica do vetor \vec{v} . Em particular $$ \vec{i} = (1,0,0); \\ \vec{j} = (0,1,0); \\ \vec{k} = (0,0,1) .$$
Observações:
1) Tendo em vista a correspondência biunívoca entre o conjunto de pontos P(x,y,z) do espaço e o conjunto de vetores \vec{v} = (x,y,z) , o espaço pode ser visto como um conjunto de pontos ou um conjunto de vetores. De certa forma um vetor no espaço é a mesma coisa de um ponto no mesmo espaço. O que nos leva a distinguir entre pontos e vetores é o fato de definirmos soma de vetores, multiplicação por escalar, produto escalar e produto vetorial.
2) Diz-se que este espaço é tridimensional, ou que tem três dimensões, porque qualquer uma de suas bases tem exatamente três vetores.
3) O sistema referencial formado pelo ponto O(0,0,0) e a base \{ \vec{i} , \vec{j} , \vec{k} \} é chamado de referencial ortonormal de origem O , ou ainda sistema cartesiano ortonormal Oxyz.
4) O \mathbb{R} ^3 é o produto cartesiano \mathbb{R} \times \mathbb{R} \times \mathbb{R} e pode ser representado pelo conjunto $$ \{ (x,y,z); x,y,z \in \mathbb{R} \}$$ e sua representação geométrica é o espaço cartesiano determinando pelos três eixos cartesianos dois a dois ortogonais Ox, Oy \text{ e } Oz .
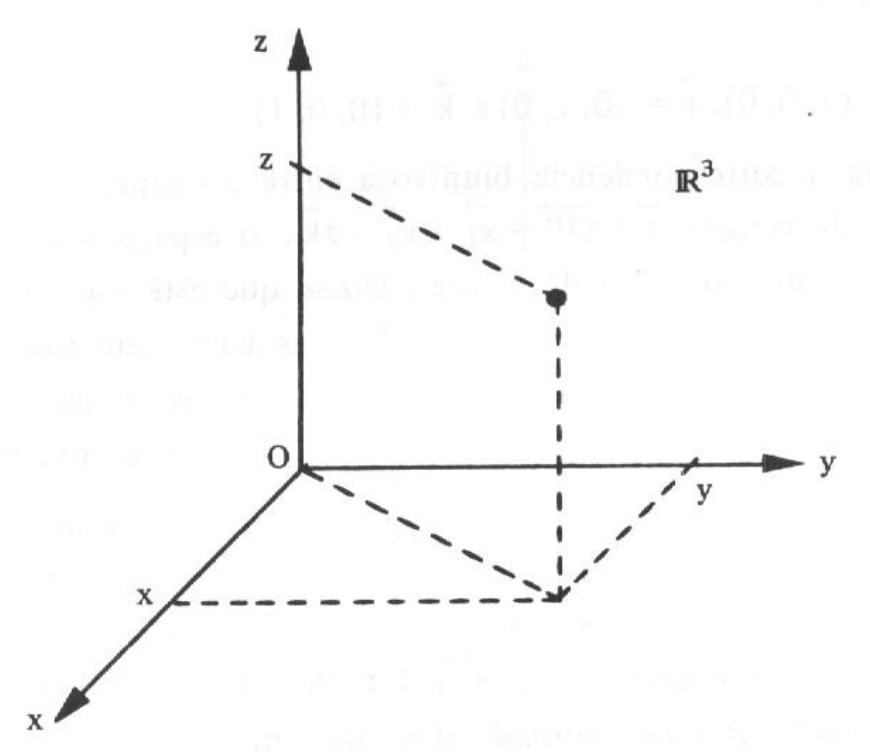
5) A distância entre dois pontos do espaço \mathbb{R}^3, P(x_1 ,y_1 ,z_1) e Q(x_2 ,y_2 ,z_2) é dada por $$ d(x,y) = \sqrt{(x_1-x_2)^2 +(y_1-y_2)^2+ (z_1-z_2)^2 } .$$ Como consequência desta definição podemos garantir que:
- A distância entre dois pontos distintos no \mathbb{R}^3 é sempre maior que zero;
- A distância entre dois pontos no \mathbb{R}^3 será nula se, e somente se, os dois pontos forem iguais;
- d(P,Q) = d(Q,P) ;
- d(P,Q) \leq d(P,R) + d(R,Q) ;
Exemplo: A equação $$ x^2 + y^2 + z^2 = 25 $$ representa o lugar dos pontos P(x,y,z) tais que a distância de P à origem é igual a 5, isto é, trata-se de uma superfície esférica de centro na origem e raio r = 5.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Igualdade – Operações – Vetor Definido por Dois Pontos
Da mesma forma como tivemos no plano, teremos no Espaço:
1) Dois vetores \vec{u} = (x_1 , y_1 , z_1 ) e \vec{v} = (x_2 , y_2 , z_2 ) são iguais se, e somente se, x_1 = x_2 , y_1 = y_2 e z_1 = z_2 ;
2) Operações Elementares no \mathbb{R} ^3 : Sejam \vec{u} = (x_1 , y_1 , z_1 ) e \vec{v} = (x_2 , y_2 , z_2 ) dois vetores do espaço \mathbb{R}^2 e \lambda um escalar qualquer. Definimos:
- \vec{u} \pm \vec{v} é um elemento do espaço \mathbb{R}^3 e $$\vec{u} \pm \vec{v} = (x_1\pm x_2, y_1\pm y_2, z_1 \pm z_2).$$ Para esta operação de adição entre vetores, podemos garantir as seguintes propriedades $$ \vec{u} + \vec{v} = \vec{v} + \vec{u} ;$$ $$ \left( \vec{u} + \vec{v} \right) + \vec{w} = \vec{u} + \left( \vec{v} + \vec{w} \right) ;$$ $$ \vec{v} + \vec{0} = \vec{v} ;$$ $$ \vec{v} + (- \vec{v} ) = \vec{0} .$$.
- o produto do escalar de \lambda com o vetor \vec{u}, denotado por \lambda \vec{u}, é um elemento do espaço \mathbb{R}^3 dado por $$\lambda \vec{u} = (\lambda x_1, \lambda y_1, \lambda z_1 )$$ Para esta operação de multiplicação por escalar, podemos garantir as seguintes propriedades $$ a ( b \vec{v} ) = (ab) \vec{v}; $$ $$ (a + b) \vec{v} ) = a \vec{v} + b \vec{v};$$ $$ a ( \vec{u} + \vec{v} ) = a \vec{u} + a \vec{v}; $$ $$ 1 \vec{v} = \vec{v} .$$
3) Se A(x_1 , y_1 , z_1) e B(x_2 , y_2 , z_2) são dois pontos quaisquer no espaço, então $$ \vec{AB} = (x_1 – x_2 , y_1 – y_2 , z_1 – z_2 ) .$$
4) Dado o vetor \vec{u} = (x , y , z ) , seu oposto é o vetor - \vec{u} = (-x , -y , -z ) que pode ser escrito como - \vec{u} = -1 \times \vec{u} = (-x , -y , -z ) .
Condição de Paralelismo de Dois Vetores
Dois vetores \vec{u} = (x_1 , y_1 , z_1 ) e \vec{v} = (x_2 , y_2 , z_2 ) são colineares (ou paralelos), existe um número k tal que \vec{u} = k \vec{v}, ou seja, $$ (x_1 , y_1 , z_1 ) = k (x_2 , y_2 , z_2 ) .$$ Logo $$ (x_1 , y_1 , z_1 ) = (k x_2 , k y_2 , k z_2 )$$ mas, pela definição de igualdade de vetores $$ x_1 = k x_2 \\ y_1 = k y_2 \\ z_1 = k z_2 $$ ou $$ \frac{x_1}{x_2} = \frac{y_1}{y_2} = \frac{z_1}{z_2} = k .$$ Esta é a condição de paralelismo de dois vetores, isto é, dois vetores são paralelos quando suas coordenadas são proporcionais. Representa-se por \vec{u} // \vec{v} .
Observação: É claro que se uma componente de um vetor é nula, a componente correspondente de um vetor paralelo também é nula.
Exemplos:
1) O vetor nulo é múltiplo de todos os outros, pois basta tomar o escalar zero. Além disso, nenhum vetor diferente do vetor nulo é seu múltiplo.
2) O vetor \vec{v} = (2,3,4) é múltiplo do vetor \vec{u} = (1,3/2,2) , pois \vec{v} = 2 \vec{u}, mas não é múltiplo do vetor \vec{w} = (1,3,2) . Logo, \vec{v} é paralelo ao vetor \vec{u} , mas não é paralelo ao vetor \vec{w}


