Vetores no R³: O Produto Misto e Duplo Produto Vetorial

Exploraremos o Produto Misto e o Duplo Produto Vetorial em Geometria Analítica tridimensional.

A Geometria Analítica no espaço tridimensional desempenha um papel fundamental na compreensão das relações geométricas entre objetos e vetores nesse contexto. Um conceito central é o Produto Misto de vetores, uma operação que permite calcular o volume de paralelepípedos formados pelos vetores em questão. Este artigo visa apresentar uma análise aprofundada do Produto Misto e sua relevância na resolução de problemas geométricos complexos.

Exploraremos as propriedades do Produto Misto, sua definição matemática e sua interpretação geométrica. Discutiremos sua utilidade na determinação de áreas e volumes de figuras geométricas tridimensionais, bem como na resolução de sistemas de equações lineares e na determinação de planos e retas. Além disso, abordaremos aplicações práticas em áreas como física, engenharia e computação gráfica.

Ao compreendermos o Produto Misto de vetores, expandimos nossas capacidades na análise do espaço tridimensional e na resolução de problemas complexos. Esta investigação visa fornecer uma visão abrangente desse conceito essencial na Geometria Analítica, destacando suas aplicações e importância na matemática e nas ciências afins.

O Espaço  \mathbb{R}^3

O \mathbb{R} ^3 é o produto cartesiano   \mathbb{R} \times \mathbb{R} \times \mathbb{R} e pode ser representado pelo conjunto $$ \{ (x,y,z); x,y,z \in \mathbb{R} \}$$ e sua representação geométrica é o espaço cartesiano determinando pelos três eixos cartesianos dois a dois ortogonais Ox, Oy \text{ e } Oz .

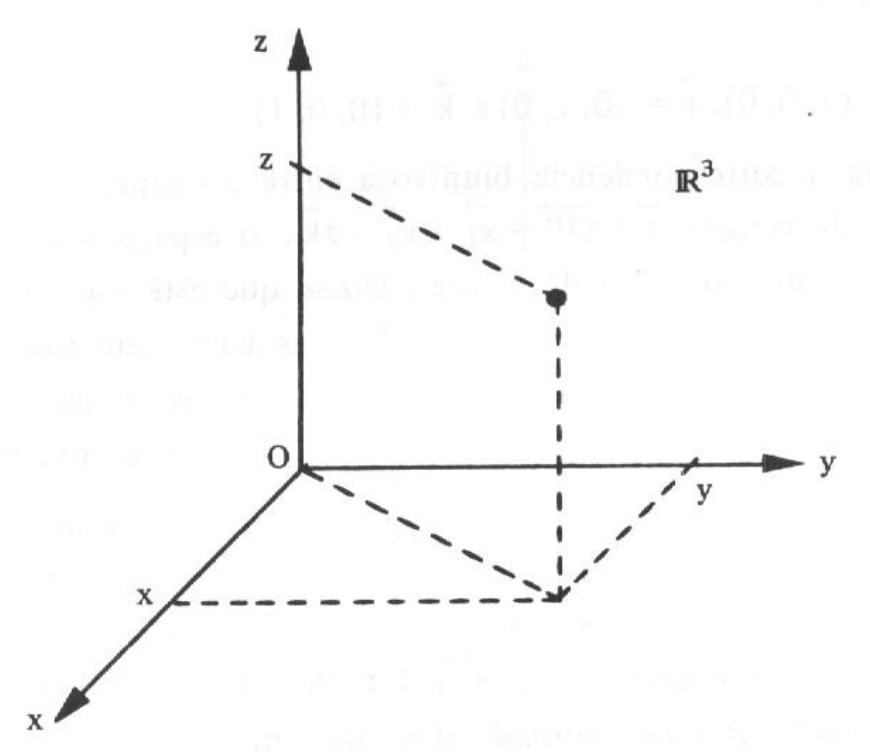
A cada ponto P do espaço vai corresponder uma terna (a,b,c) de números reais chamadas coordenadas de P e denominada abscissa, ordernada e cota, respectivamente. Cada uma destas coordenadas é obtida traçando planos paralelos aos planos coordenados,

A distância entre dois pontos do espaço \mathbb{R}^3, P(x_1 ,y_1 ,z_1) e Q(x_2 ,y_2 ,z_2) é dada por $$ d(x,y)  = \sqrt{(x_1-x_2)^2 +(y_1-y_2)^2+ (z_1-z_2)^2 } .$$ Como consequência desta definição podemos garantir que:

• A distância entre dois pontos distintos no \mathbb{R}^3 é sempre maior que zero;
• A distância entre dois pontos no \mathbb{R}^3 será nula se, e somente se, os dois pontos forem iguais;
• d(P,Q) = d(Q,P) ;
• d(P,Q) \leq d(P,R) + d(R,Q) ;

consideremos um vetor \vec{v} = x \vec{i} + y \vec{j} + z \vec{k} , onde os números reais a,b e c são números reais denominados componentes do vetor \vec{v} , na base canônica \{ \vec{i} , \vec{j} , \vec{k} \} .Analogamente como desenvolvemos no plano, este vetor \vec{v} é igual ao vetor \vec{OP} com O(0,0,0) e P(x,y,z) .

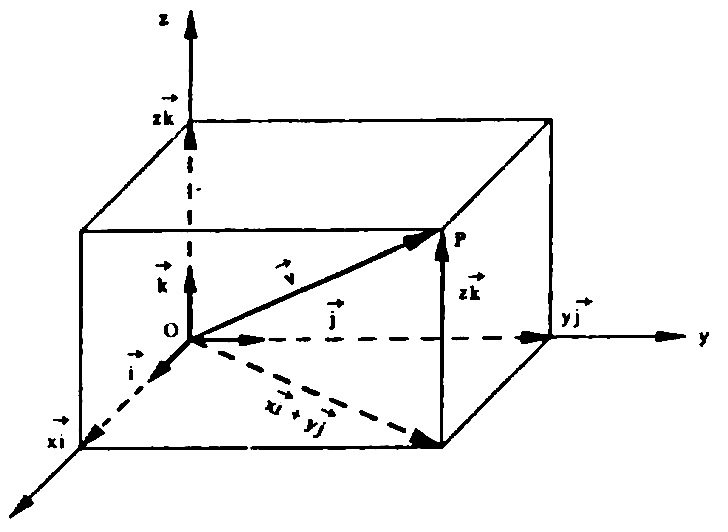
Este vetor, geometricamente, como vemos na figura anterior, irá corresponder à diagonal do paralellepípedom cujos lados são determinados pelos vetores x \vec{i} , y \vec{j} \text{ e } z \vec{k} . Para simplificar escrevemos $$ \vec{v} = (x,y,z)$$ que é a expressão analítica do vetor \vec{v} . Em particular $$ \vec{i} = (1,0,0); \\ \vec{j} = (0,1,0); \\ \vec{k} = (0,0,1) .$$

A reta com a direção do vetor \vec{i} é o eixo dos x (das abscissas), a reta com a direção do vetor \vec{j} é o eixo dos y (das ordenadas) e a reta com a direção do vetor \vec{k} é o eixo dos z (das cotas). As setas indicam o sentido de cada eixo.

O Produto Misto

O produto misto dos vetores \vec{u} , \vec{v} e \vec{w} , nesta ordem, é, por definição, o produto \vec{u} \cdot ( \vec{v} \wedge \vec{w} ) . Note-se que podemos remover os parênteses e escrever simplesmente \vec{u} \cdot \vec{v} \wedge \vec{w} , já que \vec{u} \cdot ( \vec{v} \wedge \vec{w} ) é a única interpretação possível; (\vec{u} \cdot \vec{v}) \wedge \vec{w} ) não faria sentido: seria o produto vetorial de um esclar por um vetor!

Chama-se produto misto dos vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} + z_1 \vec{k}, \qquad \vec{v} = x_2 \vec{i} + y_2 \vec{j} + z_2 \vec{k} \qquad \text{e} \qquad \vec{w} = x_3 \vec{i} + y_3 \vec{j} + z_3 \vec{k} ,$$ tomado nesta ordem, ao número real dado por \vec{u} \cdot ( \vec{v} \wedge \vec{w} ) . Indica-se o produto misto por ( \vec{u} , \vec{v} , \vec{w} ) .

Do produto vetorial temos que $$ \vec{v} \wedge \vec{w} = \left| \begin{array}{cc} y_2 &  z_2 \\ y_3 & z_3 \end{array} \right| \vec{i} – \left| \begin{array}{cc} x_2 &  z_2 \\ x_3 & z_3 \end{array} \right| \vec{j}+ \left| \begin{array}{cc} x_2 &  y_2 \\ x_3 & y_3 \end{array} \right| \vec{k}$$ e levando em consideração a definição do produto escalar de dois vetores, o valor de \vec{u} \cdot ( \vec{v} \wedge \vec{w} ) é dado por: $$ ( \vec{u} , \vec{v} , \vec{w} ) = \left| \begin{array}{cc} y_2 &  z_2 \\ y_3 & z_3 \end{array} \right| x_1 – \left| \begin{array}{cc} x_2 &  z_2 \\ x_3 & z_3 \end{array} \right| y_1 + \left| \begin{array}{cc} x_2 &  y_2 \\ x_3 & y_3 \end{array} \right| z_1 $$ e usando o Teorema de Laplace podemos encontrar a fórmula para o produto misto como o determinante $$ ( \vec{u} , \vec{v} , \vec{w} ) = \left| \begin{array}{ccc} x_1 & y_1 & z_1 \\ x_2 & y_2 &  z_2 \\ x_3 & y_3 & z_3 \end{array} \right| .$$

Exemplo: Vamos calcular o produto misto dos vetores \vec{u} = (2,3,5) , \vec{v} = (-1,3,3) e \vec{w} = (4,-3,2) . Usando a fórmula do determinante, temos que $$ ( \vec{u} , \vec{v} , \vec{w} ) = \left| \begin{array}{ccc} 2 & 3 & 5 \\-1 & 3 &  3 \\ 4 & -3 & 2 \end{array} \right| = 27.$$

As Propriedades do produto Misto

1. Condição de Coplanaridade: ( \vec{u} , \vec{v} , \vec{w} ) = 0 se um dos vetores é nulo, se dois deles são colineares, ou se três deles são coplanares.
2. Propriedade Cíclica: O produto misto independe da ordem circular dos vetores, isto é: $$ ( \vec{u} , \vec{v} , \vec{w} ) = ( \vec{w} , \vec{u} , \vec{v} ) = ( \vec{v} , \vec{w} , \vec{u} )$$Entretanto, o produto muda o sinal quando se trocam as posições de dois vetores consecutivos.
3. ( \vec{u} , \vec{v} , \vec{w} + \vec{r} ) = ( \vec{u} , \vec{v} , \vec{w}) + ( \vec{u} , \vec{v} , \vec{r} ) ;
4. ( \vec{u} , \vec{v} , m \vec{w} ) = ( \vec{u} , m \vec{v} , \vec{w} ) = ( m \vec{u} , \vec{v} ,\vec{w} ) = m ( \vec{u} , \vec{v} , \vec{w} )

Exemplos:

1) Vamos verificar se os vetores \vec{u} = (3,-1,4) , \vec{v} = (1,0,-1) e \vec{w} = (2,-1,0) são coplanares.

Os três vetores não são nunhum deles nulo, ou dois colineares, portanto, eles serão coplanares se ( \vec{u} , \vec{v} , \vec{w} ) = 0 , mas $$ ( \vec{u} , \vec{v} , \vec{w} ) = \left| \begin{array}{ccc} 3 & -1 & 4 \\1 & 0 &  -1 \\ 2 & -1 & 0 \end{array} \right| = -5 \neq 0 .$$ Portanto, estes vetores não são coplanares.

2) Vamos verificar se os pontos A(1,2,4) , B(-1,0,-2) , C(0,2,2) e  D(-2,1,-3) estão no mesmo plano.

Os quatro pontos dados são coplanares se forem coplanares os vetores \vec{AB} = (-2,-2,-6) , \vec{AC} = (-1,0,-2) e \vec{AD} = (-3,-1,-7) , ou seja, se ( \vec{AB} , \vec{AC} , \vec{AD} ) = 0 . Como $$ ( \vec{AB} , \vec{AC} , \vec{AD} ) = \left| \begin{array}{ccc} -2 & -2 & -6 \\ -1 & 0 &  -2 \\ -3 & -1 & -7 \end{array} \right| = 0 $$ então podemos afiramr que estes quatro pontos são coplanares.

Interpretação Geométrica do Módulo do Produto Misto

Geometricamente, o produto misto ( \vec{u} , \vec{v} , \vec{w} ) é igual, em módulo, ao volume do paralelepípedo de arestas determinadas pelos vetores \vec{u} = \vec{AD} , \vec{v} = \vec{AB} e \vec{w} = \vec{AC} , conforme a figura abaixo:

Todo paralelepípedo é equivalente a dois prismas triangulares igual. Como todo prisma triângular equivale a três pirâmides (que no caso são tetraedros) de base e altura equivalentes à base e altura do prisma, o volume de cada uma destas pirâmides é 1/6 do volume do paralelepípedo. Sendo A , B , C e D quatro pontos do espaço não coplanares, e três a três não colineares como na figura abaixo, as arestas so paralelepípedo são determinadas pelos vetores \vec{u} = \vec{AD} , \vec{v} = \vec{AB} e \vec{w} = \vec{AC} e, portanto, o volume do tetraedro ABCD é $$ V = \frac{1}{6} | ( \vec{AB} , \vec{AC} , \vec{AD} ) | .$$

Exemplo: Calcular o volume do tetraedro cujos vértices são A (1,2,1) , B (7,4,3) , C (4,6,2) e D (3,3,3) .

Solução: O volume do tetraedro é dado por $$ V = \frac{1}{6} | ( \vec{AB} , \vec{AC} , \vec{AD} ) | $$ sendo $$ \vec{AB} = (6,2,2) $$ $$ \vec{AC} = (3,4,1) $$ $$ \vec{AD} = (2,1,2) $$ e $$( \vec{AB} , \vec{AC} , \vec{AD} ) = \left| \begin{array}{ccc} 6 & 2 & 2 \\ 3 & 4 &  1 \\ 2 & 1 & 2 \end{array} \right| = 24 . $$ Portanto, o volume do tetraedro é: $$ V = \frac{1}{6} 24 = 4 \text{ u. v.} $$

O Duplo Produto Vetorial

Dados os vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} + z_1 \vec{k}, \qquad \vec{v} = x_2 \vec{i} + y_2 \vec{j} + z_2 \vec{k} \qquad \text{e} \qquad \vec{w} = x_3 \vec{i} + y_3 \vec{j} + z_3 \vec{k} ,$$ tomado nesta ordem, a vetor dado por \vec{u} \wedge ( \vec{v} \wedge \vec{w} ) chama-se duplo produto vetorial dos vetores \vec{u} , \vec{v} e \vec{w}

Observação: Tendo em vista que o produto vetorial não é associativo, em geral, \vec{u} \wedge ( \vec{v} \wedge \vec{w} ) \neq (\vec{u} \wedge  \vec{v} ) \wedge \vec{w}  .

Uma Fórmula para o cálculo do Duplo Produto Vetorial:

Uma fórmula para o cálculo do duplo produto vetorial pode ser dada como $$ \vec{u} \wedge ( \vec{v} \wedge \vec{w} ) = \left| \begin{array}{cc} \vec{v} & \vec{w} \\ \vec{u} \cdot \vec{v} & \vec{u} \cdot \vec{w} \end{array} \right| $$

Exemplo: Considerando $$ \vec{u} = (3,-2,6) \qquad \vec{v} = (2,-1,0) \qquad \text{e} \qquad \vec{w} = (1,3,4) ,$$ temos que $$ \vec{u} \cdot \vec{v} = 8 $$ $$ \vec{u} \cdot \vec{w} = -27 ,$$ logo,  $$ \vec{u} \wedge ( \vec{v} \wedge \vec{w} ) = \left| \begin{array}{cc} \vec{v} & \vec{w} \\ 8 & -21 \end{array} \right| =  -21 (2,-1,0) – 8 (1,3,4) = (-50,-3,-32). $$

Leia Mais:

• Vetores No R³: Um guia ilustrado dos vetores no espaço euclidiano
• Vetores no R³: O Produto Escalar e suas Interpretações Geométricas
• Vetores no R³: O Produto Vetorial e suas Interpretações Geométricas