Vetores no R³: O Produto Escalar e suas Interpretações Geométricas

Este artigo aborda o produto escalar de vetores no espaço tridimensional ( \mathbb{R}^3 ) um objeto de aplicações práticas e importância em várias disciplinas científicas e engenharias.

A matemática desempenha um papel fundamental em várias disciplinas científicas e engenharias, e os vetores no espaço tridimensional, \mathbb{R}^3 , são uma ferramenta essencial nesse contexto. Neste artigo, exploraremos de forma abrangente o produto escalar de vetores em \mathbb{R}^3 , suas propriedades e interpretações geométricas.

Compreender o produto escalar é crucial para a resolução de uma ampla gama de problemas do mundo real, desde análises de forças em sistemas mecânicos até cálculos de ângulos e projeções em geometria espacial. Ao longo deste artigo, vamos desvendar as nuances do produto escalar e mostrar como ele é aplicado em diferentes contextos. Prepare-se para uma jornada matemática que ampliará seus horizontes e aprofundará seu entendimento sobre vetores em \mathbb{R}^3 .

O Espaço  \mathbb{R}^3

O \mathbb{R} ^3 é o produto cartesiano   \mathbb{R} \times \mathbb{R} \times \mathbb{R} e pode ser representado pelo conjunto $$ \{ (x,y,z); x,y,z \in \mathbb{R} \}$$ e sua representação geométrica é o espaço cartesiano determinando pelos três eixos cartesianos dois a dois ortogonais Ox, Oy \text{ e } Oz .

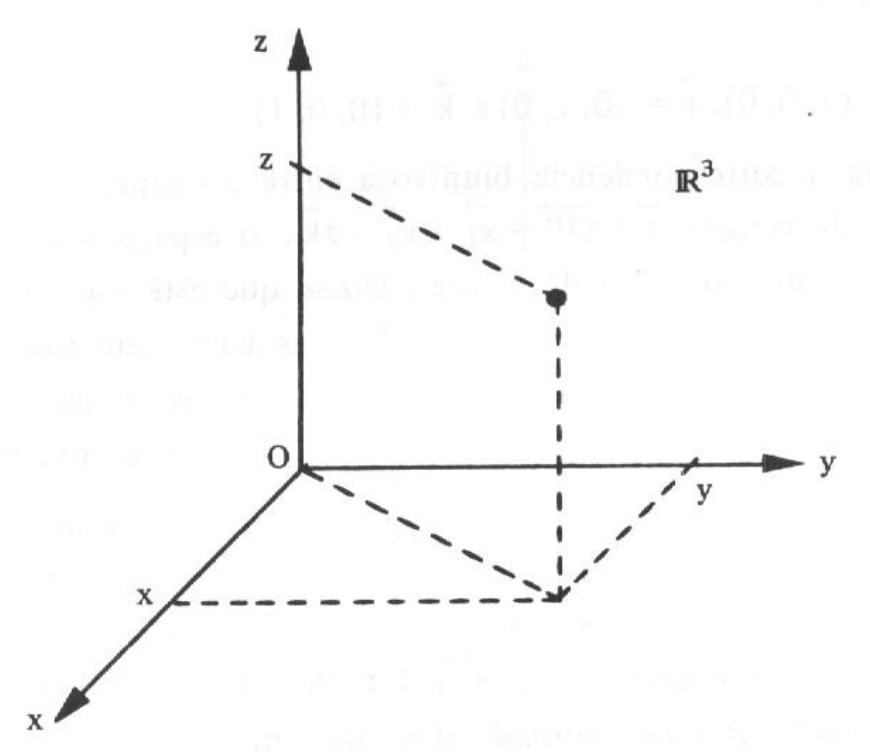
A cada ponto P do espaço vai corresponder uma terna (a,b,c) de números reais chamadas coordenadas de P e denominada abscissa, ordernada e cota, respectivamente. Cada uma destas coordenadas é obtida traçando planos paralelos aos planos coordenados,

A distância entre dois pontos do espaço \mathbb{R}^3, P(x_1 ,y_1 ,z_1) e Q(x_2 ,y_2 ,z_2) é dada por $$ d(x,y)  = \sqrt{(x_1-x_2)^2 +(y_1-y_2)^2+ (z_1-z_2)^2 } .$$ Como consequência desta definição podemos garantir que:

• A distância entre dois pontos distintos no \mathbb{R}^3 é sempre maior que zero;
• A distância entre dois pontos no \mathbb{R}^3 será nula se, e somente se, os dois pontos forem iguais;
• d(P,Q) = d(Q,P) ;
• d(P,Q) \leq d(P,R) + d(R,Q) ;

consideremos um vetor \vec{v} = x \vec{i} + y \vec{j} + z \vec{k} , onde os números reais a,b e c são números reais denominados componentes do vetor \vec{v} , na base canônica \{ \vec{i} , \vec{j} , \vec{k} \} .Analogamente como desenvolvemos no plano, este vetor \vec{v} é igual ao vetor \vec{OP} com O(0,0,0) e P(x,y,z) .

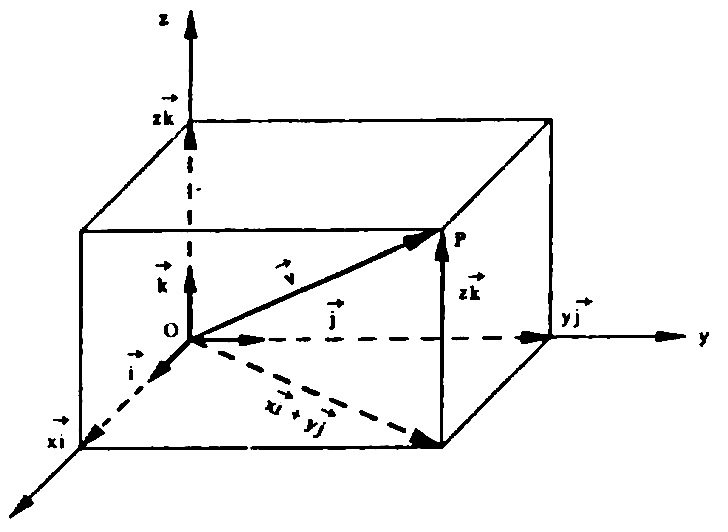
Este vetor, geometricamente, como vemos na figura anterior, irá corresponder à diagonal do paralellepípedom cujos lados são determinados pelos vetores x \vec{i} , y \vec{j} \text{ e } z \vec{k} . Para simplificar escrevemos $$ \vec{v} = (x,y,z)$$ que é a expressão analítica do vetor \vec{v} . Em particular $$ \vec{i} = (1,0,0); \\ \vec{j} = (0,1,0); \\ \vec{k} = (0,0,1) .$$

A reta com a direção do vetor \vec{i} é o eixo dos x (das abscissas), a reta com a direção do vetor \vec{j} é o eixo dos y (das ordenadas) e a reta com a direção do vetor \vec{k} é o eixo dos z (das cotas). As setas indicam o sentido de cada eixo.

A Norma de um Vetor no Espaço

Dado um ponto P( x, y,z) , o comprimento do segmento de reta \overline{OP} é igual a $$ \sqrt{x^2 + y^2+z^2} .$$ Diremos também que este é o comprimento do vetor \vec{OP} = \vec{v} e escrevemos $$ | \vec{v} | = | \vec{OP} | = | (x,y,z)| = \sqrt{x^2 + y^2+z^2} .$$ Se | \vec{v} | = 1 então diremos que \vec{v} é um vetor unitário.

EXEMPLO: Se \vec{v} = (2,1,0) então $$ | \vec{v} |= \sqrt{2^2 + 2^2+0^2} = \sqrt{5} $$.

EXEMPLO (versor de um vetor \vec{u} ): O versor do vetor \vec{u} = (a,b,c) é o vetor \vec{v} , dado por $$ \vec{v} = \frac{1}{| \vec{u} |} \vec{u} = \frac{1}{\sqrt{a^2 +b^2+c^2}} (a,b,c) = \left( \frac{a}{\sqrt{a^2 +b^2+c^2}} , \frac{b}{\sqrt{a^2 +b^2+c^2}}, \frac{c}{\sqrt{a^2 +b^2+c^2}} \right).$$ O versor do vetor \vec{u} é um vetor unitário, com mesma direção e sentido de \vec{u} . De fato, podemos mostrar facilmente que o versor de \vec{u} é unitário: $$ |  \vec{v} | = \left| \frac{a}{\sqrt{a^2 +b^2+c^2}} , \frac{b}{\sqrt{a^2 +b^2+c^2}}, \frac{c}{\sqrt{a^2 +b^2+c^2}} \right| = \\ =  \sqrt{ \left( \frac{a}{\sqrt{a^2 +b^2+c^2}} \right)^2 + \left( \frac{b}{\sqrt{a^2 +b^2+c^2}} \right)^2 + \left( \frac{c}{\sqrt{a^2 +b^2+c^2}} \right)^2} = \\ = \sqrt{\frac{a^2}{a^2 +b^2+c^2} + \frac{b^2}{a^2 +b^2 +c^2}  + \frac{c^2}{a^2 +b^2 +c^2} } = \\ = \sqrt{\frac{a^2 + b^2+c^2}{a^2 +b^2+c^2}} = \sqrt{1} = 1.$$

OBSERVAÇÕES:

1. O Versor de um vetor: O versos de um vetor \vec{v} é um vetor \vec{u} , unitário, com a mesma direção e o mesmo sentido de \vec{v} . Portanto o versor de um vetor \vec{v} é dado pela fórmula $$ \vec{u} = \frac{1}{| \vec{v} |} \vec{v}.$$
2. A Distância entre dois pontos: a distância d entre dois pontos A \left( x_1 , y_1 , z_1 \right) e B \left( x_2 , y_2 , z_2 \right)   é definida como a norma, ou o módulo, do vetor \vec{AB} , ou seja $$ d(A,B) = | \vec{AB}| = |B-A| = \sqrt{ \left( x_2 – x_1 \right)^2+ \left( y_2 – y_1 \right)^2 + \left(z_2 – z_1 \right)^2}.$$

O Produto Escalar (ou Produto Interno Usual) no \mathbb{R}^3 :

O produto escalar de dois vetores é um número, à partir do qual se pode exprimir a distância entre dois pontos, o ângulo entre duas retas orientadas e, em particular, seu perpendicularismo. A dedução do produto escalar e de suas propriedades básicas se torna mais fácil quando ele é expresso em coordenadas

Chama-se produto escalar (ou produto interno usual) de dois vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} + z_1 \vec{k} \qquad \text{e} \qquad \vec{v} = x_2 \vec{i} + y_2 \vec{j} + z_2 \vec{k} $$ e se representa por \vec{u} \cdot \vec{v} , ao número real $$  \vec{u} \cdot \vec{v} = x_1 x_2 + y_1 y_2 + z_1 z_2.$$ O produto escalar de \vec{u} por \vec{v} também é indicado por \langle \vec{u} , \vec{v} \rangle e se lê ” \vec{u} escalar \vec{v} “. Observando que se \vec{v} = (x,y,z) e $$ \vec{v} \cdot \vec{v} = x^2 + y^2 + z^2$$ então podemos escrever que $$ | \vec{v} |= \sqrt{ \vec{v} \cdot \vec{v} }.$$

EXEMPLO: Se \vec{u} = (3,-5,8) e \vec{v} =(4,-2,-1) tem-se \vec{u} \cdot \vec{v} = 3 \times 4 + -5 \times (-2) + 8 \times (-1) = 12 + 10 -8= 14 .

Propriedades do Produto Escalar

Para quaisquer que sejam os vetores $$ \vec{u} = x_1 \vec{i} + y_1 \vec{j} + z_1 \vec{k} \qquad  \vec{v} = x_2 \vec{i} + y_2 \vec{j} + z_2 \vec{k} \qquad \text{e} \qquad \vec{w} = x_3 \vec{i} + y_3 \vec{j} + z_3 \vec{k}, \qquad \alpha \in \mathbb{R} $$ temos que:

1. \vec{u} \cdot \vec{u} \geq 0 e \vec{u} \cdot \vec{u} = 0 se, e somente se, \vec{u} = \vec{0} ;
2. \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u} ;
3. \vec{u} \cdot \left( \vec{v} + \vec{w} \right)= \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w};
4. \left( \alpha \vec{u} \right) \cdot \vec{v} = \alpha \left( \vec{u} \cdot \vec{v}  \right) = \vec{u} \cdot \left( \alpha \vec{v} \right) ;
5. \vec{u} \cdot \vec{u} = | \vec{u} | ^2 .

OBSERVAÇÃO 1: Ao definirmos o produto escalar de dois vetores por meio de suas coordenadas, devemos nos perguntar se o produto escalar se alteraria caso tomássemos outra base ortonormal para o espaço euclidiano \mathbb{R} ^3 . O teorema que enunciaremos abaixo, que nos dá a fórmula para calcular o ângulo entre dois vetores no espaço nos autoriza a dizer que o produto interno se mantem inalterado por ser o produto dos tamanhos dos vetores com o cosseno do ângulo entre os dois vetores. Um exemplo interessante deste fato se encontra no livro “Coordenadas no Espaço”, de Elon Lages Lima (confira o livro neste link).

OBSERVAÇÃO 2: Diz-se que $$| \vec{u} – \vec{v} |^2 = (\vec{u} – \vec{v}) \cdot (\vec{u} – \vec{v}) = d(P,Q)^2 ,$$ onde P é a extremidade de \vec{u} e onde Q é a extremidade de \vec{v} , ambos tomados com origem  na origem do sistema, é a distância do vetor \vec{u} ao vetor \vec{v} .

A Interpretação Geométrica do Produto Escalar de Dois Vetores

Vamos dar o significado geométrico do produto escalar entre dois vetores.

1) FÓRMULA PARA O ÂNGULO ENTRE DOIS VETORES:

Teorema: Se \theta é o ângulo entre os vetores \vec{u} e \vec{v} , então \vec{u} \cdot \vec{v} =| \vec{u} | | \vec{v} | \text{cos} ( \theta ) .

Portanto, por este Teorema podemos concluir que o ângulo entre os vetores \vec{u} e \vec{v} é dado por $$ \theta = \text{arc cos}\left( \frac{\vec{u} \cdot \vec{v}}{| \vec{u} | | \vec{v} |} \right).$$

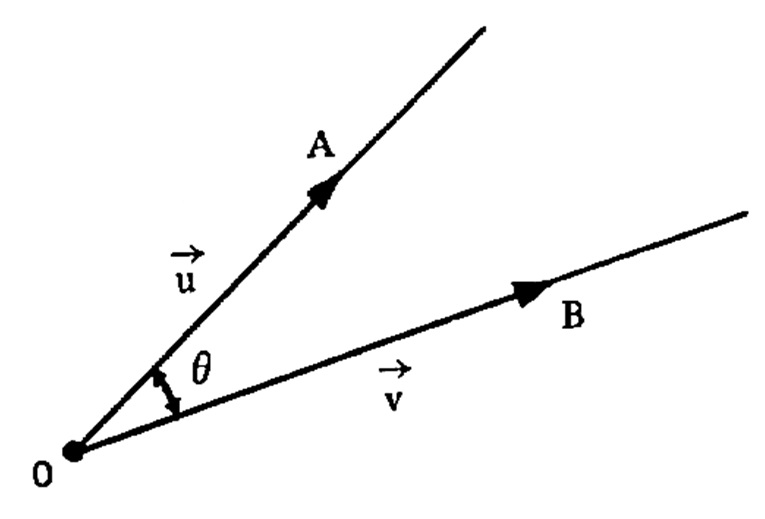
O ângulo de dois vetores   \vec{u} e   \vec{v} não nulos é o ângulo \theta formado pelas semi-retas OA e OB , tal que 0 \leq \theta \leq \pi , como na figura abaixo:

OBSERVAÇÕES:

1. Se \theta = \pi , então   \vec{u} e   \vec{v} têm a mesma direção e sentidos opostos;
2. Se \theta = 0 , então   \vec{u} e   \vec{v} têm a mesma direção e o mesmo sentido;
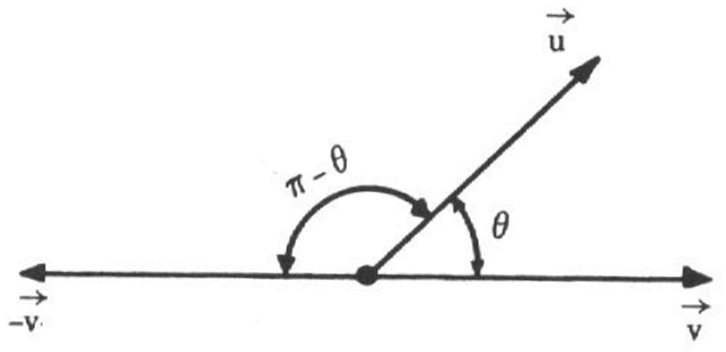
3. O ângulo formado pelos vetores   \vec{u} e - \vec{v} é o suplemento do ângulo de   \vec{u} e   \vec{v} , como na figura abaixo:
   

   

4. Se \theta = \dfrac{\pi}{2} , então   \vec{u} e   \vec{v} são ortogonais e indica-se \vec{u} \bot \vec{v} ; Neste caso, o triângulo retângulo OBC permite escrever $$ | \vec{u} + \vec{v} | ^2 = | \vec{u} | ^2 + | \vec{v} |^2 .$$
5. O vetor nulo é ortogonal a qualquer vetor;
6. Se   \vec{u} é ortogonal a   \vec{v} e m é um número real qualquer,   \vec{u} é ortogonal a   m \vec{v} .

EXEMPLO: Vamos calcular o ângulo entre os vetores   \vec{u} = (1,1,4) e   \vec{v} = (-1,2,2). Usando a fórmula para o ângulo entre vetores obtemos: $$ \vec{u} \cdot \vec{v} =| \vec{u} | | \vec{v} | \text{cos} ( \theta ) \Leftrightarrow (1,1,4) \cdot (-1,2,2) = \sqrt{1^2 + 1^2 + 4^2} \sqrt{(-1)^2 + 2^2 + 2^2} \text{cos} ( \theta )  \Leftrightarrow \\ \Leftrightarrow -1 +2 +8 = \sqrt{18} \sqrt{9} \text{cos} ( \theta )  \Leftrightarrow \\ \Leftrightarrow\text{cos} ( \theta ) = \frac{9}{3 \sqrt{2} \times 3} = \frac{\sqrt{2}}{2}.$$ Portanto, $$ \theta = \frac{\pi}{4}.$$

2) CONDIÇÃO DE PERPENDICULARISMO ENTRE DOIS VETORES:

Teorema: Os vetores \vec{u} e \vec{v} são perpendiculares se, e somente se, \vec{u} \cdot \vec{v} = 0 .

Uma demonstração deste teorema pode ser feita rapidamente da seguinte maneira:

( \Rightarrow ) Como \vec{u} e \vec{v} são perpendiculares, então, pelo Teorema de Pitágoras nos dá $$ | \vec{u} + \vec{v} |^2 = | \vec{u} |^2 + | \vec{v} |^2.$$ Mas, $$ | \vec{u} + \vec{v} |^2 = \left( \vec{u} + \vec{v} \right) \cdot \left( \vec{u} + \vec{v} \right) = | \vec{u} |^2 + |\vec{v}|^2 + 2 \vec{u} \cdot \vec{v}.$$ Desta forma, $$  | \vec{u} |^2 + | \vec{v} |^2 = | \vec{u} |^2 + |\vec{v}|^2 + 2 \vec{u} \cdot \vec{v}.$$ Logo, $$ 2 \vec{u} \cdot \vec{v} = 0 \Rightarrow  \vec{u} \cdot \vec{v} = 0.$$ Portanto, se  \vec{u} e \vec{v} são perpendiculares então \vec{u} \cdot \vec{v} = 0 .

( \Leftarrow ) Por outro lado, se \vec{u} \cdot \vec{v} = 0 . então o ângulo entre estes dois vetores satifaz a condição $$ \vec{u} \cdot \vec{v} =| \vec{u} | | \vec{v} | \text{cos} ( \theta ) \Rightarrow 0 = | \vec{u} | | \vec{v} | \text{cos} ( \theta ).$$ Se | \vec{u} | = 0 ou  | \vec{v} | = 0 então um deles, ou ambos, é o vetor nulo, portanto são perpendiculares. Supondo agora que | \vec{u} | \neq 0 ou  | \vec{v} | \neq 0 , então nenhum deles pode ser o vetor nulo e ainda teremos que $$ \text{cos} ( \theta ) = 0 \Rightarrow \theta = \frac{ \pi }{2} .$$ Portanto, o ângulo entre os vetores é reto, garantindo a perpendicularidade entre \vec{u} e \vec{v} .

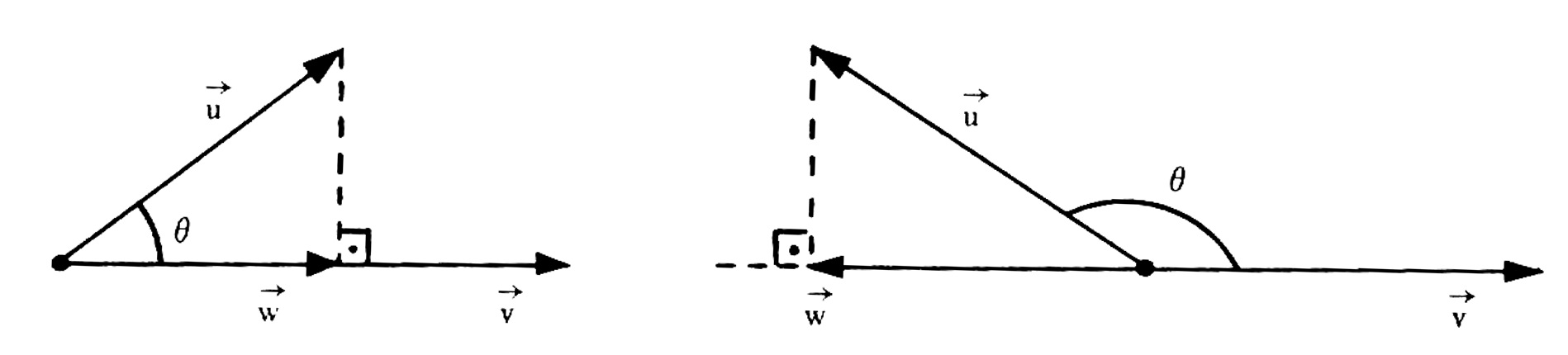
3) PROJEÇÃO ORTOGONAL DE VETORES NO ESPAÇO:

Sejam \vec{u} e \vec{v} , ambos vetores não-nulos, e \theta o ângulo formado entre eles. Então o vetor $$ \vec{w} = \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} $$ é a projeção de \vec{u} sobre \vec{v} .

A notação usual da a projeção de \vec{u} sobre \vec{v} é dada por $$ \text{proj}_{\vec{v}} \vec{u} =  \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} = \left( \frac{\vec{u} \cdot \vec{v}}{\vec{v} \cdot \vec{v}} \right) \vec{v}$$  e esta projeção de vetores é representada nas figuras abaixo.

EXEMPLO: Determine o vetor projeção de \vec{u} = (2,3,4) sobre \vec{v} = (1, -1, 0) . Utilizando a fórmula: $$ \vec{w} = \left( \frac{\vec{u} \cdot \vec{v}}{| \vec{v} | ^2} \right) \vec{v} = \left( \frac{(2,3,4) \cdot (1, -1, 0)}{(1,-1,0) \cdot (1, -1, 0)} \right) (1,-1,0) = \\ = \left( \frac{2-3+0}{1+1+0} \right) (1,-1,0) = \left( – \frac{1}{2} , \frac{1}{2} , 0  \right).$$

4) ÂNGULOS DIRETORES E COSSENOS DIRETORES:

Sejam \vec{v}=(x,y,z) um vetor não-nulo. Os ângulos diretores de \vec{v} são os ângulos \alpha, \beta e \gamma que este vetor foma com os vetores \vec{i} ,  \vec{j} e \vec{k} . Os cossenos diretores de \vec{v} são os cossenos de seus ângulos diretores, ou seja \text{cos} (\alpha), \text{cos} ( \beta ) e \text{cos} ( \gamma )

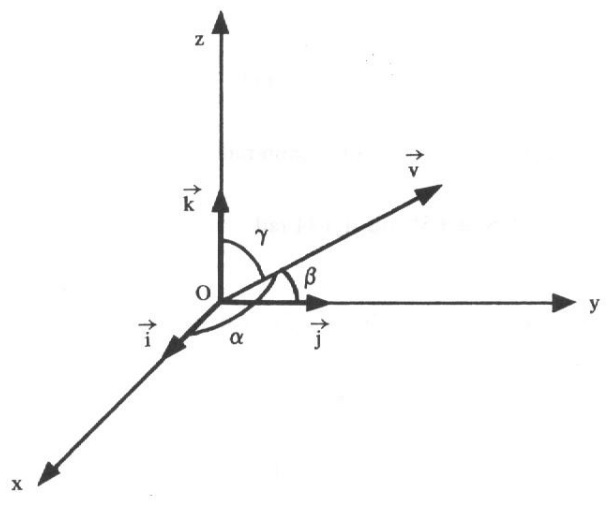
Para o cálculo dos cossenos diretores deduzimos, à partir da fórmula do ângulo entre vetores, que: $$ \text{cos} (\alpha) = \frac{x}{| \vec{v} | }, \qquad \text{cos} (\beta) = \frac{y}{| \vec{v} | }, \qquad \text{cos} (\gamma) = \frac{z}{| \vec{v} | }$$

Observe que as componentes do versor do vetor \vec{v} são os cossenos diretores deste vetor. De fato, basta observar que o versor de \vec{v} é dado por $$ \text{versor de } \vec{v} = \frac{\vec{v} }{|\vec{v}|} = \left( \frac{\vec{x} }{|\vec{v}|} ,  \frac{\vec{y} }{|\vec{v}|} , \frac{\vec{z} }{|\vec{v}|}\right).$$ Ou seja, $$ \text{versor de } \vec{v} = ( \text{cos} (\alpha), \text{cos} (\beta), \text{cos} (\gamma) ).$$

Além disso, como o versor de \vec{v} é unitário então $$ | \text{versor de } \vec{v} | = \sqrt{ \text{cos} (\alpha) ^2 + \text{cos} (\beta) ^2 + \text{cos} (\gamma) ^2}=1$$ Portanto, a soma dos quadrados dos cossenos diretores de um vetor é sempre igual a 1.

EXEMPLO: Calcule os cossenos diretores e os ângulos diretores do vetor \vec{v} = (6,-2,3) . Observe que a norma deste vetor é $$| \vec{v}| = \sqrt{6^2 + (-2)^2+ 3^2} = \sqrt{36+4+9}= 7$$ logo, o versor de \vec{v} é o vetor $$ \text{versor de } \vec{v} = \left( \frac{6}{7} , \frac{-2}{7}, \frac{3}{7} \right),$$ portanto, os cossenos diretores são dados por $$ \text{cos} (\alpha) =\frac{6}{7}, \qquad   \text{cos} (\beta) = \frac{-2}{7}, \qquad e \text{cos} (\gamma) = \frac{3}{7} .$$ Desta forma, encontramos como ângulos diretores $$ \alpha = \text{arc cos} \left( \frac{6}{7} \right) \approx 31º $$ $$ \beta = \text{arc cos} \left( \frac{-2}{7} \right) \approx 107º $$ $$ \gamma = \text{arc cos} \left( \frac{36}{7} \right) \approx 65º $$

Leia Mais:

• Vetores No R³: Um guia ilustrado dos vetores no espaço euclidiano
• Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano
• Vetores no Plano R²: Norma e Produto Escalar
• O que é um Vetor? Um guia ilustrado dos vetores no espaço.