Vetor Gradiente | Definição, Campo Gradiente e Exercícios Resolvidos

Campos Escalares, ou Funções de Várias Variáveis a Valores Vetoriais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar.

Nesse artigo queremos estabelecer o conceito de Vetor Gradiente para esse tipo de função.

Vamos apresentar esse conceito através de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.

O Vetor Gradiente

Seja z=f(x,y) uma função que admite derivadas parcias em (x_0, y_0). O vetor $$\nabla f(x_0, y_0) = \left(\frac{\partial f}{\partial x}(x_0, y_0), \frac{\partial f}{\partial y}(x_0, y_0) \right)$$ denomina-se vetor gradiente de f em (x_0, y_0). Geometricamente, interpretamos o gradiente como um vetor aplicado no ponto (x_0, y_0).

Se estamos trabalhando com um ponto genérico (x,y), usualmente representamos o vetor gradiente de f por $$\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$$

EXEMPLO

Seja f(x,y) = x^2 + y^2. Calcule \nabla f (1,1) e represente-o geometricamente.

Temos que

• \nabla f (1,1) = \left(\frac{\partial f}{\partial x}(1, 1), \frac{\partial f}{\partial y}(1, 1) \right).
• \nabla f (1,1) = \left(2.1, 2.1 \right)=(2,2)

De maneira análoga, podemos definir o vetor gradiente para uma função com três variáveis. Seja w=f(x,y,z) uma função que admite derivadas parcias em (x_0, y_0,z_0). O vetor gradiente de f no ponto (x_0, y_0,z_0) é dado por $$\nabla f(x_0, y_0,z_0) = \left(\frac{\partial f}{\partial x}(x_0, y_0,z_0), \frac{\partial f}{\partial y}(x_0, y_0,z_0), \frac{\partial f}{\partial z}(x_0, y_0,z_0)\right)$$

EXEMPLO Determinar o vetor gradiente da função w=xyz^2.

Calculando as derivadas parciais obtemos:

$$\nabla f(x, y,z) = \left(yz^2 ,xz^2 ,2xyz \right)$$

Observações sobre o Vetor Gradiente

O gradiente armazena todas as informações da derivada parcial de uma função multivariável.

Porém, ele é mais do que um simples dispositivo de armazenamento: ele tem diversas interpretações maravilhosas e muitos usos:

• O vetor \nabla f te diz em qual direção a função f cresce mais rapidamente partindo do ponto em que está aplicado;
• \nabla f é uma função vetorial de várias variáveis, ou seja, é um campo vetorial;
• O vetores \nabla f são perpendiculares às curvas de nível da função f;
• Esse símbolo, \nabla , é chamado de nabla ou del. Tipicamente, nabla se refere ao próprio símbolo enquanto del se refere à operação que ele representa. Isso pode ser confuso, porque del também pode se referir ao símbolo \partial.
• o operador \nabla pode ser considerado, livremente, como um vetor dos operadores parciais da derivada: $$ \nabla = \left(\frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2},…, \frac{\partial }{\partial x_n}\right)$$

Interpretação Geométrica do Gradiente de Uma Função de Duas Variáveis

Geometricamente, \nabla f (x_0, y_0) é um vetor normal à curva de nível f (x, y) = c, em (x_0, y_0) . A reta passando por (x_0, y_0) e perpendicular a \nabla f (x_0, y_0) denomina-se reta tangente, em (x_0, y_0) , à curva de nível f (x, y) = c,. A equação desta reta é $$\nabla f (x_0, y_0) . [(x,y) – (x_0, y_0)] = 0,$$ ou seja, $$ \frac{\partial f}{\partial x}(x_0, y_0)  [x – x_0] + \frac{\partial f}{\partial y}(x_0, y_0)  [y – y_0] = 0.$$

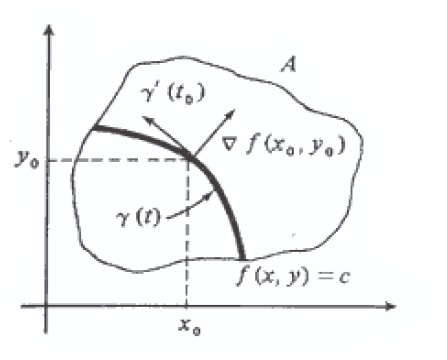
OBSERVAÇÃO: Se y = g(x) é uma função diferenciável que é dada implicitamente pela equação f(x,y) = 0 , onde f é suposta diferenciável e \nabla f (x_0, y_0) \neq \vec{0} , com y_0 = g(x_0) . Segue que, para todo x no domínio de g , f(x,g(x)) = 0 , isto é, a imagem da curva \gamma (x) = (x, g(x)) está contida na curva de nível f(x,g(x)) = 0 . Assim, \nabla f (x_0, y_0) é normal ao gráfico de g(x) no ponto (x_0, y_0) . Além disso, se $$ \frac{\partial f}{\partial x}(x_0, y_0) \neq 0 \;\;\;e\;\;\; \frac{\partial f}{\partial y}(x_0, y_0) \neq 0,$$ podemos estabelecer que $$ g’ (x_0) = – \frac{ \frac{\partial f}{\partial x}(x_0, y_0)}{ \frac{\partial f}{\partial y}(x_0, y_0)}$$ é o coeficiente angular da reta tangente ao gráfico de g(x) no ponto (x_0 , y_0) .

EXEMPLO: Considere y = g(x) é uma função diferenciável definida implicitamente pela equação y^3 + xy + x^3 = 3x . Queremos determinar as equações das retas tangentes e normal ao gráfico de g no ponto (1,1).

Observe que y^3 + xy + x^3 = 3x \Leftrightarrow y^3 + xy + x^3 - 3x = 0. Desta forma, f(x,y) = y^3 + xy + x^3 = 3x e \nabla f(1,1) é perpendicular ao gráfico de f no ponto (1,1) . Temos: $$ \nabla f(x,y) = (y + 3x^2 – 3, 3y^2 + x) $$ assim \nabla f(1,1) = (1,4) .

Logo, a reta tangente ao gráfico de g no ponto (1,1) e dá pela equação $$\nabla f (1, 1) . [(x,y) – (1, 1)] = 0 \Leftrightarrow (1,4).(x-1, y-1) = 0 \Leftrightarrow y = – \frac{1}{4}x + \frac{5}{4}.$$

Já a reta normal é dada pela equação vetorial $$ (x,y) = (1,1) + t (1,4),$$ pois esta é uma reta que passa por (1,1) na direção do vetor \nabla f(1,1) = (1,4) , que é normal ao gráfico de g(x),, o que nos leva a $$x = 1 + t$$ $$y = 1 + 4t,$$ logo y = 1 + 4(x-1)\Leftrightarrow y = 4x -3 .

Interpretação Geométrica do Gradiente de Uma Função de Três Variáveis

Seja f(x,y,z) de classe C^1 num aberto A \subset \mathbb{R} ^3 e seja (x_0 , y_0 , z_0 ) um ponto da superfície de nível f(x,y,z) = c . Suponha que \nabla f (x_0, y_0 , z_0) \neq \vec{0} .

Pode-se provar que \nabla f (x_0, y_0 , z_0) é normal em (x_0, y_0 , z_0) a toda curva diferenciável \gamma passando por este ponto e com imagem contida na superfície f(x,y,z) = c .

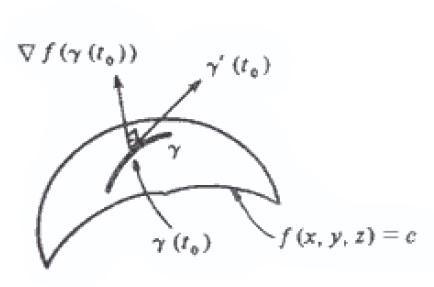
O plano que passa pelo ponto (x_0, y_0 , z_0) e tem o vetor \nabla f (x_0, y_0 , z_0) como normal é exatamente o plano tangente em (x_0, y_0 , z_0) à superfície f(x,y,z) = c .

A equação deste plano tangente pode ser escrito pela equação $$\nabla f (x_0, y_0 , z_0) . [(x,y,z) – (x_0, y_0 , z_0)] = 0.$$

E a reta $$(x,y,z) = (x_0 , y_0 , z_0 )+ \lambda \nabla f (x_0 , y_0 , z_0 ), \;\;\; \lambda \in \mathbb{R}$$ denomina-se reta normal, em  (x_0, y_0 , z_0) à superfície f(x,y,z) = c .

Mais sobre teoria e exemplos de plano tangente e reta normal ao gráfico de uma função de várias variáveis você lê neste nosso artigo.

O Campo Gradiente

Seja z=f(x_1, x_2,..., x_n) uma função definida num conjunto aberto A \in \mathbb{R} ^n tal que as derivadas parciais existam. Definimos o vetor gradiente de f por $$\nabla f (x_1, x_2,…, x_n) = \left(\frac{\partial f}{\partial x_1} (x_1, x_2,…, x_n) , \frac{\partial f}{\partial x_2} (x_1, x_2,…, x_n) , … , \frac{\partial f}{\partial x_n} (x_1, x_2,…, x_n) \right).$$

Observe que \nabla f é uma função vetorial de várias variáveis, ou seja, é um campo vetorial.

Neste caso, o operador \nabla pode ser considerado, livremente, como um vetor dos operadores parciais da derivada: $$ \nabla = \left(\frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2},…, \frac{\partial }{\partial x_n}\right)$$

Nos espaços \mathbb{R} ^2 e \mathbb{R} ^3 o vetor gradiente pode ser escrito como $$\nabla f = \left(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} \right) = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} $$ $$\nabla f = \left(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} \right) = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z} \vec{k}$$ onde \{ \vec{i}, \vec{j} \} e \{ \vec{i}, \vec{j} , \vec{k} \} são, respectivamente, os vetores das bases canônicas de \mathbb{R} ^2 e \mathbb{R} ^3 .

EXEMPLO

Considere a função f(x,y) = x^2 + y^2 .

As curvas de nível desta função são circunferências centradas na origem cujos raios crescem à partir da origem.

Como vimos no artigo sobre o Vetor Gradiente, o vetor \nabla f são perpendiculares às curvas de nível da função f.

Desta forma, como $$ \nabla f = \left( 2x , 2y \right) = 2 (x,y)$$ o campo vetorial gradiente neste caso é formado por vetores com tamanho dado pelo dobro da distância do ponto (x,y), onde o vetor está aplicado, à origem, ou seja, à medida que o ponto se afasta da origem o comprimento do gradiente cresce e fica igual a duas vezes a distância do ponto à origem.

Isso pode ser visto na representação gráfica abaixo:

EXEMPLO

Considere a função f(x,y) = x^2 - y^2 .

As curvas de nível desta função são hipérboles e como $$ \nabla f = \left( 2x , – 2y \right) = 2 (x,y),$$ então o campo vetorial gradiente neste caso é formado por vetores que crescem, ficando igual a duas vezes a distância do ponto à origem, à medida que o ponto se afasta da origem.

Isso pode ser visto na representação gráfica abaixo:

Exercícios Resolvidos:

1) Encontre a equação da reta perpendicular à curva x^2 + y^2 = 4 , no ponto P(1, \sqrt{3}) .

SOLUÇÃO: Ou seja, queremos encontrar a equação da reta normal à curva x^2 + y^2 = 4 , que é uma circunferência com centro na origem e raio igual a 2, no ponto P(1, \sqrt{3}) .

Esta reta é aquela que passa por P(1, \sqrt{3}) (facilmente verificado como um ponto da curva) na direção do vetor \nabla f(1, \sqrt{3}) , onde $$f(x,y) = x^2 + y^2 – 4,$$ afinal, \nabla f(x,y) é perpendicular ao gráfico de y = g(x) dada implicitamente por f(x,y) = 0 .

Assim, a reta procurada é dada por $$ (x,y) = (1, \sqrt{3}) + \lambda \nabla f(1, \sqrt{3}) = (x,y) = (1, \sqrt{3}) + \lambda (2, 2/ \sqrt{3}).$$

Leia Mais:

• Plano Tangente e Reta Normal | Funções de Várias Variáveis
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Várias Variáveis Reais a Valores Reais ou Campos Escalares
• EFEITO BORBOLETA | Edward Lorenz e a Teoria do Caos
• GRÁFICOS | Da Análise Estatística ao Mercado de Ações