Plano Tangente e Reta Normal | Funções de Várias Variáveis

Nesse artigo queremos estabelecer o conceito de Plano Tangente e Reta Normal para funções de várias variáveis a valore reais. O plano tangente ao gráfico de uma função num ponto é o plano que contem todas as retas tangentes ao gráfico de f que passam pelo ponto. Se todas as retas tangente a esse ponto não são co-planares, então dizemos que o plano tangente não existe.

Em suma, um plano tangente a uma função de duas variáveis é um plano que é tangente ao seu gráfico, definido por uma equação de várias variáveis, linear, que dá a equação de um plano em cada ponto específico do domínio da função, se ela for diferenciável nestes pontos.

Campos Escalares, ou Funções de Várias Variáveis a Valores Reais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar.

Vamos apresentar esse conceito através de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.

Plano Tangente

Seja f diferenciável no ponto (x_0, y_0). O plano $$z-f(x_0, y_0) = \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0) $$ denomina-se plano tangente ao gráfico de f no ponto \left( x_0, y_0, f(x_0, y_0) \right).

OBSERVAÇÃO

• Só definimos o plano tangente em \left( x_0, y_0, f(x_0, y_0) \right) se a função f é diferenciável no ponto (x_0, y_0). Se a função não for diferenciável, mas adimitir derivadas parciais no ponto, o plano existirá, mas não será o plano tangente.
• O plano tangente contem todas as retas tangentes ao gráfico de f no ponto (x_0, y_0, f(x_0, y_0)).

EXEMPLO

Seja f(x,y) = 3x^2y-x. Determine a equação do plano tangente ao gráfico de f no ponto \left( 1, 2, f(1,2) \right).

Temos que

\begin{eqnarray*}
\frac{\partial f}{\partial x}(x, y) & = & 6xy-1\\
\frac{\partial f}{\partial x}(1, 2) & = & 6(1)(2)-1 = 11\\
\\
\\
\frac{\partial f}{\partial y}(x, y) & = & 3x^2-x\\
\frac{\partial f}{\partial y}(1, 2) & = & 3(1)^2-1 = 3\\
\\
\\
f(1,2) & = & 3(1)^2(2)-1 = 5
\end{eqnarray*}

Podemos, facilmente notar que as derivadas parciais de f(x,y) existem e são contínuas em qualquer ponto do plano \mathbb{R} ^2.

Assim, f é diferenciável no ponto (1,2) e o plano tangente ao gráfico de f neste ponto é dado por $$z-f(1,2) = 11(x-1)+3(y-2) \Rightarrow z-5 = 11(x-1)+3(y-2). $$

EXEMPLO

Considere a função $$f(x,y) = \left\{ \begin{array}{lll}
\frac{xy^2}{x^2+y^2} ; (x,y) & \neq & (0,0)\\
\\
0; (x,y) & = & (0,0) \end{array} \right.$$ O gráfico de f admite plano tangente em (0,0,f(0,0))?

Temos que

$$\frac{\partial f}{\partial x}(0, 0) = \lim_{h \rightarrow 0}{\frac{f(0+h,0)-f(0,0)}{h}} = \lim_{h \rightarrow 0}{\frac{0 – 0}{h}} =0$$

$$\frac{\partial f}{\partial y}(0, 0)= \lim_{h \rightarrow 0}{\frac{f(0,0+h)-f(0,0)}{h}} = \lim_{h \rightarrow 0}{\frac{0 – 0}{h}} =0$$
e
$$ L = \lim_{(x,y) \rightarrow (0, 0)}{ \frac{f(x,y) – \left( f(x_0, y_0) + \frac{\partial f}{\partial x} (x_0 , y_0) (x-x_0) + \frac{\partial f}{\partial y} (x_0 , y_0) (y-y_0) \right)}{\| (x,y) – (x_0, y_0) \|}} =$$

$$ = \lim_{(x,y) \rightarrow (0, 0)}{ \frac{\frac{xy^2}{x^2+y^2} – (0 +0(x-0)+0(y-0)}{\sqrt{x^2+y^2}}} =$$

$$ = \lim_{(x,y) \rightarrow (0, 0)}{\frac{xy^2}{(x^2+y^2)^{\frac{3}{2}}} }$$

Considere a curva passando pela origem dada por G(t)=(t,t). Daí

\begin{eqnarray*}
L & = & \lim_{(x,y) \rightarrow (0, 0)}{\frac{xy^2}{(x^2+y^2)^{\frac{3}{2}}} }\\
& = & \lim_{(x,y) \rightarrow (0, 0)}{\frac{t^3}{(2t^2)^{\frac{3}{2}}}}\\
& = & \lim_{(x,y) \rightarrow (0, 0)}{\frac{t^3}{\sqrt{8t^6}}}\\
& = & \lim_{(x,y) \rightarrow (0, 0)}{\frac{t^3}{t^3 . 2\sqrt{2}}}\\
& = & \frac{1}{2\sqrt{2}} \neq 0\\
\end{eqnarray*}

E ainda, para a curva F(t)=(0,y) temos que L = \lim_{(x,y) \rightarrow (0, 0)}{\frac{0}{(y^2)^{\frac{3}{2}}} } = 0.

Portanto, o limite $$\lim_{(x,y) \rightarrow (0, 0)}{ \frac{f(x,y) – \left( f(x_0, y_0) + \frac{\partial f}{\partial x} (x_0 , y_0) (x-x_0) + \frac{\partial f}{\partial y} (x_0 , y_0) (y-y_0) \right)}{\| (x,y) – (x_0, y_0) \|}}$$ não existe e, por consequência, a função f(x,y) não é diferenciável no ponto (0,0) e assim não possui plano tangente neste ponto.

Reta Normal

A reta que passa pelo ponto (x_0,y_0, f(x_0,y_0)) e é paralela ao vetor $$\left( \frac{\partial f}{\partial x}(x_0 , y_0), \frac{\partial f}{\partial y}(x_0 , y_0 ), -1 \right)$$ denomina-se reta normal ao gráfico de f no ponto (x_0, y_0,f(x_0, y_0,)).

Assim, a equação de tal reta é dada por $$(x,y,z) = (x_0, y_0,f(x_0, y_0,)) + \lambda \left( \frac{\partial f}{\partial x}(x_0 , y_0), \frac{\partial f}{\partial y}(x_0 , y_0 ), -1 \right). $$

O vetor $$\left( \frac{\partial f}{\partial x}(x_0 , y_0), \frac{\partial f}{\partial y}(x_0 , y_0 ), -1 \right)$$ é o vetor normal ao plano tangente do gráfico de f no ponto (x_0, y_0,f(x_0, y_0,)).

EXEMPLO

Seja f(x,y) = 3x^2y-x. Determine a equação da reta normal ao gráfico de f no ponto \left( 1, 2, f(1,2) \right).

Temos que

\begin{eqnarray*}
\frac{\partial f}{\partial x}(x, y) & = & 6xy-1\\
\frac{\partial f}{\partial x}(1, 2) & = & 6(1)(2)-1 = 11\\
\\
\\
\frac{\partial f}{\partial y}(x, y) & = & 3x^2-x\\
\frac{\partial f}{\partial y}(1, 2) & = & 3(1)^2-1 = 3\\
\\
\\
f(1,2) & = & 3(1)^2(2)-1 = 5
\end{eqnarray*}

Daí, a equação da reta normal ao gráfico de f no ponto \left( 1, 2, f(1,2) \right) é $$(x,y,z) = (1, 2, 5) + \lambda \left( 11, 3, -1 \right). $$

Gradiente, Plano Tangente e Reta Normal

Seja f(x,y,z) de classe C^1 num aberto A \subset \mathbb{R} ^3 e seja (x_0 , y_0 , z_0 ) um ponto da superfície de nível f(x,y,z) = c . Suponha que \nabla f (x_0, y_0 , z_0) \neq \vec{0} .

Pode-se provar que \nabla f (x_0, y_0 , z_0) é normal em (x_0, y_0 , z_0) a toda curva diferenciável \gamma passando por este ponto e com imagem contida na superfície f(x,y,z) = c .

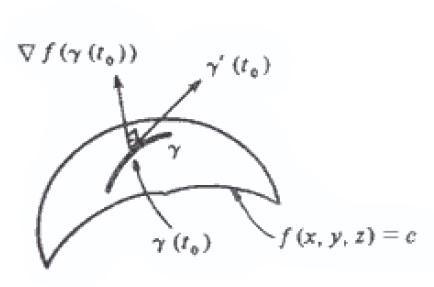
O plano que passa pelo ponto (x_0, y_0 , z_0) e tem o vetor \nabla f (x_0, y_0 , z_0) como normal é exatamente o plano tangente em (x_0, y_0 , z_0) à superfície f(x,y,z) = c .

A equação deste plano tangente pode ser escrito pela equação $$\nabla f (x_0, y_0 , z_0) . [(x,y,z) – (x_0, y_0 , z_0)] = 0.$$

E a reta $$(x,y,z) = (x_0 , y_0 , z_0 )+ \lambda \nabla f (x_0 , y_0 , z_0 ), \;\;\; \lambda \in \mathbb{R}$$ denomina-se reta normal, em  (x_0, y_0 , z_0) à superfície f(x,y,z) = c .

Exercícios Resolvidos

• Plano Tangente e Reta Normal | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• A Regra da Cadeia Para Funções de Várias Variáveis
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Várias Variáveis Reais a Valores Reais ou Campos Escalares

Assista Nossa Vídeo-Aula Sobre Plano Tangente e Reta Normal: