Um campo vetorial é uma função vetorial de várias variáveis onde o domínio e a imagem estão no mesmo espaço espaço euclidiano. Sejam m e n dois naturais diferentes de zero. Uma função de n variáveis reais a valores vetoriais em \mathbb{R}^m é uma função f:A\rightarrow \mathbb{R}^m, onde A é um subconjunto não vazio de \mathbb{R}^n, denominado domínio de f. Ou seja, para os campos vetoriais, temos uma função deste tipo, onde m = n.
Os termos aplicação e transformação são sinônimos de função e várias vezes são utilizadas para diferenciar as funções vetoriais de várias variáveis das demais.
| Mais abaixo, neste artigo, temos uma vídeo-aula e uma lista com vários exercícios resolvidos sobre Campos Vetoriais. |
O QUE É UM CAMPO VETORIAL?
Seja A um subconjunto do \mathbb{R}^n e \vec{F} uma transformação de A em \mathbb{R}^n. Se para cada ponto de A o associarmos ao vetor \vec{F} iremos nos referir a \vec{F} como um campo vetorial.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
No espaço \mathbb{R}^3, considere P(x,y,z) um ponto de um conjunto de pontos do espaço. Se para cada ponto P deste conjunto associarmos um vetor \vec{F}(P) = \vec{F}(x,y,z), então obtemos um campo vetorial para estes pontos e \vec{F}(x,y,z) é denominada função vetorial.
Em coordenadas cartesianas, $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ onde i = (1,0,0), j = (0,1,0) e k = (0,0,1) e F_i : \mathbb{R}^3 \rightarrow \mathbb{R}
Exemplos Gráficos de Campos Vetoriais
O nome campo vetorial se justifica se expressarmos graficamente \vec{F} do seguinte modo: em cada ponto u \in A desenhamos um vetor de tamanho e direção de \vec{F} (u) com a origem em u
Campo vetorial gerado pelos vetores tangentes à curva em um ponto
Campo de vetores normais a uma superfície
Campo Vetorial gerado pela equação diferencial ordinária que modela o pêndulo Plano
Campo Vetorial sobre a esfera
Seja um fluido percorrendo um encanamento com fluxo constante. Se associamos a cada ponto a velocidade do fluido nesse ponto, obtemos um campo de vetores de velocidades do fluido.
Uma superfície metálica é aquecida por um lado de tal modo que perde calor pelo outro; a forma que flui o calor na placa define um campo de vetores que vai das regiões mais quentes para as mais frias.
A corrente elétrica fluindo através de um fio induz um campo de vetores ao redor do fio, chamado campo magnético.
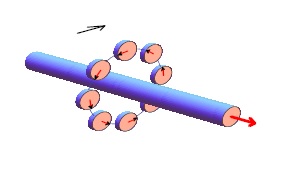
Mais Exemplos Sobre Campos Vetoriais
EXEMPLO 1
Vamos representar geometricamente o campo vetorial \vec{F}(x,y) = j
Este campo vetorial é constante e associa a cada ponto do plano o vetor j=(0,1) aplicado em (x,y).
EXEMPLO 2 (Campo Vetorial Tangente ao Círculo de Raio r>0 e Centrado na Origem)
Considere o campo vetorial $$\vec{F}(x,y) = \left( -\frac{y}{x^2+y^2} ,\frac{x}{x^2+y^2} \right).$$
Em coordenadas polares o campo vetorial é dado por $$\vec{F}(r,\theta) = \frac{1}{r}\left( -\sin{\theta} ,\cos{\theta}\right); \qquad r>0$$ e é representado por
Este campo vetorial tem direção igual à do vetor tangente ao círculo de raio r>0 centrado na origem.
Observe que \| \vec{F}(r,\theta) \| \rightarrow + \infty se r \rightarrow 0 e \| \vec{F}(r,\theta) \| \rightarrow 0 se r \rightarrow + \infty .
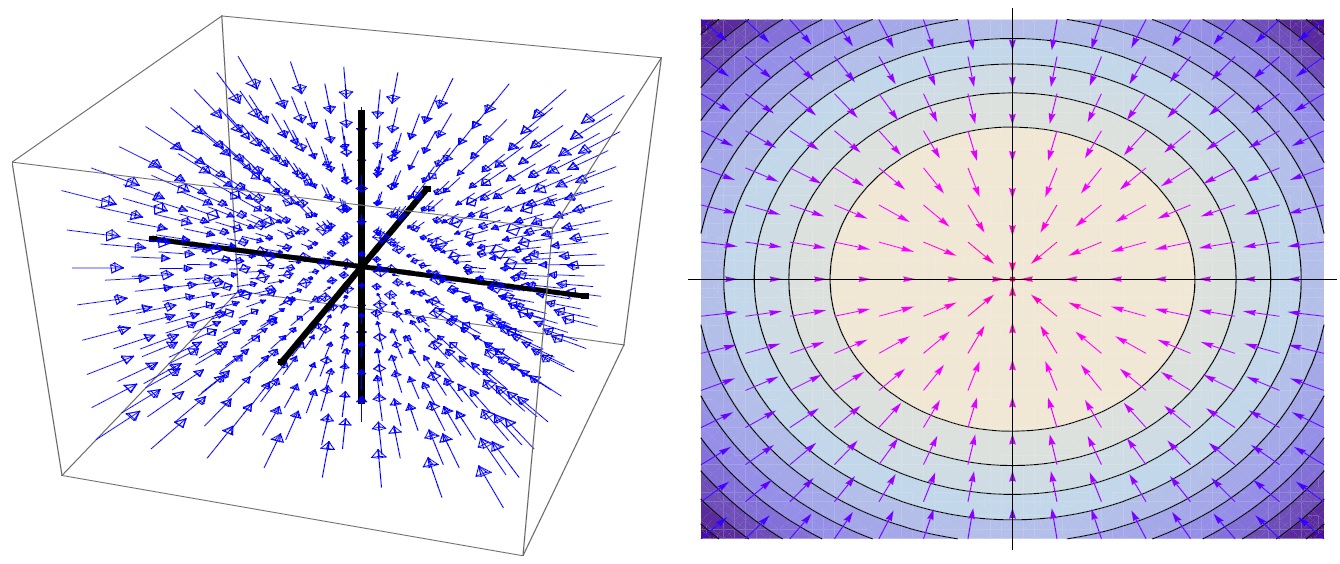
EXEMPLO 3 (Campo Radial de Quadrado Inverso)
Seja o campo de posição P(x,y,z) . Definimos o seguinte campo: $$ \vec{F} (x,y,z) = \frac{k}{\| P(x,y,z) \| ^3 } P(x,y,z) ,$$ sendo k \in \mathbb{R} . Se k < 0 então este campo vetorial apontará para a origem do sistema de coordenadas.
Este campo é denominado campo radial de quadrado inverso e não está definido, obviamente, na origem do sistema de coordenadas.
Observe que quanto mais afastado da origem está P(x,y,z) menor é a norma do campo \vec{F} (x,y,z) .
Além disso, podemos observar por $$ \| \vec{F} (x,y,z) \|= \frac{|k|}{\| P(x,y,z) \| ^2 }$$ que a norma do campo \vec{F} (x,y,z) é inversamente proporcional ao quadrado da distância da origem ao ponto (x,y,z).
São exemplos de campos radiais de quadrado inverso: 1) a força exercida sobre una partícula de massa m descrita nas condições da lei da gravitação universal de Newton; e 2) o campo elétrico gerado por uma partícula carregada e regido pela lei de Coulomb.
Campo Radial de Quadrado Inverso com k = −1 e sua projeção no plano.
Continuidade e Diferenciabilidade de um Campo Vetorial
Como todo campo vetorial é um caso particular das funções vetoriais de várias variáveis, podemos definir a continuidade e a diferenciabilidade deste tipo de função de modo direto.
Seja A um subconjunto do \mathbb{R}^n. O campo vetorial \vec{F}A \rightarrow \mathbb{R}^n é dito contínuo, diferenciável ou de classe C^k em u \in A se todas as suas funções coordenadas $$ F_i : A \subset \mathbb{R}^n \rightarrow \mathbb{R} $$ são contínuas, diferenciáveis ou de classe C^k , respctivamente.
Se para cada ponto de A o associarmos ao vetor \vec{F} iremos nos referir a \vec{F} como um campo vetorial.
O Campo Gradiente
Seja z=f(x_1, x_2,..., x_n) uma função definida num conjunto aberto A \in \mathbb{R} ^n tal que as derivadas parciais existam. Definimos o vetor gradiente de f por $$\nabla f (x_1, x_2,…, x_n) = \left(\frac{\partial f}{\partial x_1} (x_1, x_2,…, x_n) , \frac{\partial f}{\partial x_2} (x_1, x_2,…, x_n) , … , \frac{\partial f}{\partial x_n} (x_1, x_2,…, x_n) \right).$$
Observe que \nabla f é uma função vetorial de várias variáveis, ou seja, é um campo vetorial.
Neste caso, o operador \nabla pode ser considerado, livremente, como um vetor dos operadores parciais da derivada: $$ \nabla = \left(\frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2},…, \frac{\partial }{\partial x_n}\right)$$
Nos espaços \mathbb{R} ^2 e \mathbb{R} ^3 o vetor gradiente pode ser escrito como $$\nabla f = \left(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} \right) = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} $$ $$\nabla f = \left(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} \right) = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z} \vec{k}$$ onde \{ \vec{i}, \vec{j} \} e \{ \vec{i}, \vec{j} , \vec{k} \} são, respectivamente, os vetores das bases canônicas de \mathbb{R} ^2 e \mathbb{R} ^3 .
EXEMPLO
Considere a função f(x,y) = x^2 + y^2 .
As curvas de nível desta função são circunferências centradas na origem cujos raios crescem à partir da origem.
Como vimos no artigo sobre o Vetor Gradiente, o vetor \nabla f são perpendiculares às curvas de nível da função f.
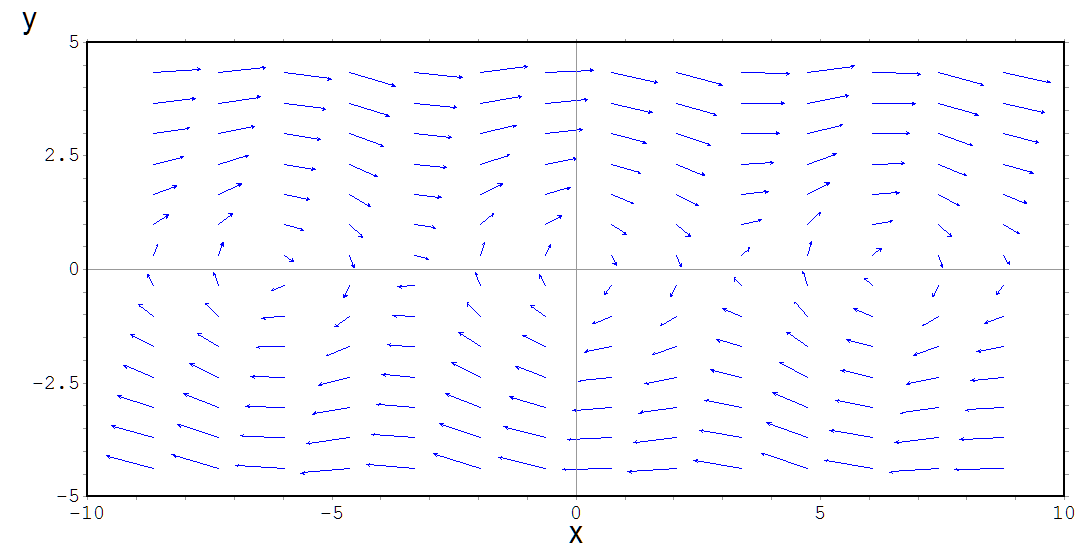
Desta forma, como $$ \nabla f = \left( 2x , 2y \right) = 2 (x,y)$$ o campo vetorial gradiente neste caso é formado por vetores com tamanho dado pelo dobro da distância do ponto (x,y), onde o vetor está aplicado, à origem, ou seja, à medida que o ponto se afasta da origem o comprimento do gradiente cresce e fica igual a duas vezes a distância do ponto à origem.
Isso pode ser visto na representação gráfica abaixo:
EXEMPLO
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Considere a função f(x,y) = x^2 - y^2 .
As curvas de nível desta função são hipérboles e como $$ \nabla f = \left( 2x , – 2y \right) = 2 (x,-y),$$ então o campo vetorial gradiente neste caso é formado por vetores que crescem, ficando igual a duas vezes a distância do ponto à origem, à medida que o ponto se afasta da origem.
Isso pode ser visto na representação gráfica abaixo:
Campos Conservativos:
Um campo vetorial \vec{F}(x,y): \Omega \subset \mathbb{R}^n \rightarrow \mathbb{R}^n denomina-se conservativo se existe um campo escalar diferenciável \varphi: \Omega \rightarrow \mathbb{R} tal que
\begin{equation}
\nabla \varphi = \vec{F}\;\;\;em\;\;\;\Omega. \label{conservativo}
\end{equation}
Portanto, um campo vetorial é conservativo se é um campo gradiente.
Uma função \varphi que satisfaz essa igualdade denomina-se função potencial de \vec{F}.
EXEMPLO
Considere \vec{F}(x,y) = \frac{x}{x^2+y^2} i + \frac{y}{x^2+y^2} j se (x,y)\neq(0,0) é conservativo?
Se este campo vetorial for conservativo, existirá uma função \varphi(x,y) de modo que $$\nabla \varphi (x,y) = \left( \frac{\partial \varphi}{\partial x}, \frac{\partial \varphi}{\partial y} \right) = \left( \frac{x}{x^2+y^2} , \frac{y}{x^2+y^2} \right) = \vec{F}(x,y).$$ Desta forma, $$\frac{x}{x^2+y^2} = \frac{\partial \varphi}{\partial x} \Rightarrow \varphi(x,y) = \frac{1}{2}\ln{(x^2+y^2)}+g(y).$$
Daí, $$\frac{\partial \varphi}{\partial y} = \frac{y}{x^2+y^2}+g'(y) \Rightarrow g'(y) = 0 \Rightarrow g(y) = c. $$
Portanto, tomando $$\varphi(x,y) = \frac{1}{2}\ln{(x^2+y^2)} +c$$ podemos mostrar que o campo vetorial é conservativo.
Listas de Exercícios Resolvidos
Leia Mais:
- Campos Vetoriais Conservativos e Potencial
- Campo Vetorial | O que são as Curvas de Fluxo ou Curvas Integrais?
- O Rotacional de um Campo Vetorial | Definição e Interpretação Geométrica
- O Divergente de um Campo Vetorial | Definição e Interpretação
- Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano
Video-Aula Sobre Campos Vetoriais:
