Limite de Funções de Várias Variáveis Reais

Campos Escalares, ou Funções de Várias Variáveis a Valores Vetoriais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar. Nesse artigo queremos estabelecer o conceito de Limite para esse tipo de função.

Quando consideramos funções de duas variáveis, seu domínios são conjuntos de pontos (x,y) do plano, que podem ser o plano todo ou conjuntos mais restritos, como retângulos, elipses, semiplanos, quadrantes, etc.

Com isso, é necessário, diversas vezes, distinguir entre os pontos internos e pontos de fronteira do conjunto, por isso precisaremos introduzir, à priori, alguns conceitos topológicos.

A Topologia dos Espaços R² e R³

Antes da definição de limites para funções de duas ou mais variáveis se faz necessária a definição de alguns conceitos básicos quanto a topologia dos espaços \mathbb{R} ^2 e \mathbb{R} ^3.

DEFINIÇÃO (Vizinhança ou Bola Aberta)

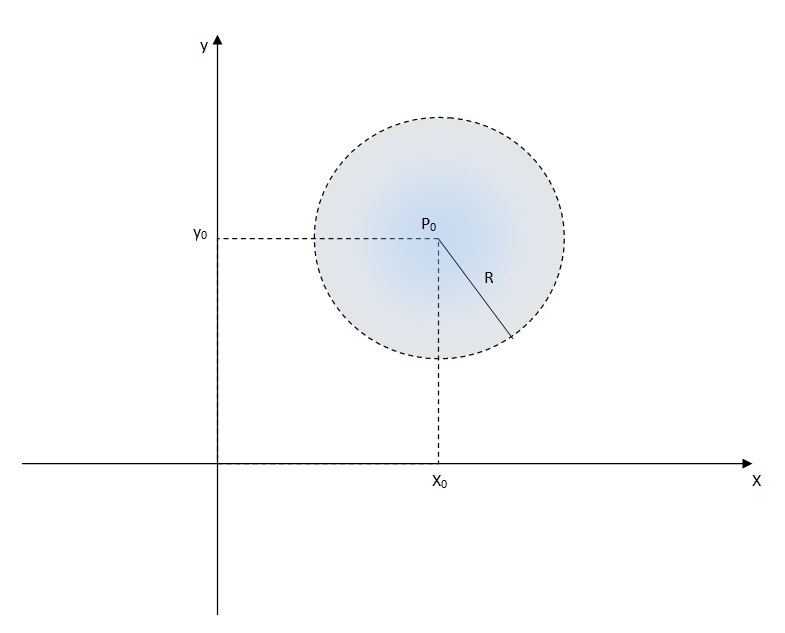
Dado um ponto P_0 \in \mathbb{R}^n e um número \delta >0, denominamos de vizinhança de P_0, que se indica por V_{\delta} (P_0 ), ou bola aberta B \left( P_0 , \delta \right) , ao conjunto de pontos P \in \mathbb{R}^n, cuja distância a P_0 seja menor do que \delta.

Ou seja, no \mathbb{R} ^2,

$$B \left( P_0 , \delta \right) = \left\{ (x,y) \in \mathbb{R}^2 ; \| (x,y) – (x_0, y_0) \| < \delta \right\}.$$

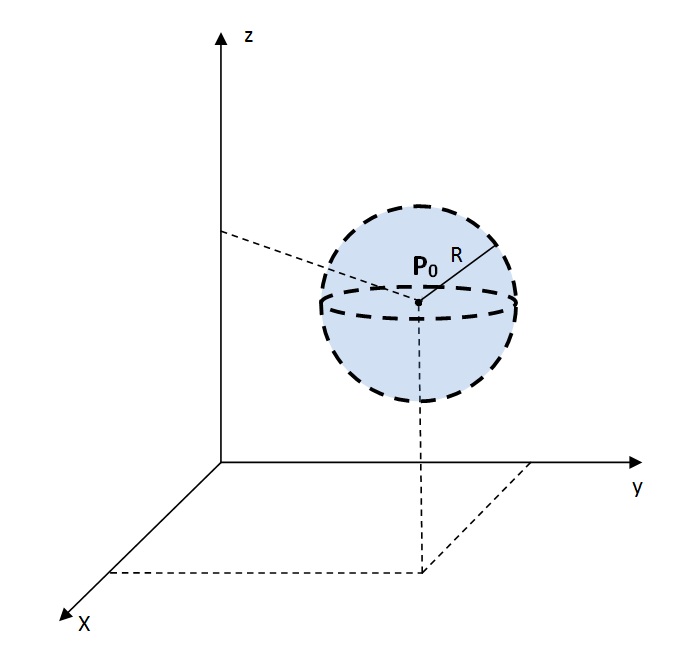
No caso do espaço \mathbb{R} ^3 a vizinhaça de V_{\delta} (P_0), ou a bola aberta B(P_0, \delta), para um ponto P_0 (x_0,y_0,z_0) é definida pela condição

$$B \left( P_0 , \delta \right) = \left\{ (x,y,z) \in \mathbb{R}^3 ; \| (x,y,z) – (x_0, y_0,z_0) \| < \delta \right\}.$$

EXEMPLO

O conjunto abaixo representa a vizinhança dos pontos do plano que distam menos de 1 da origem.

\begin{eqnarray*}
B \left( (0,0) , 1 \right) & = & \left\{ (x,y) \in \mathbb{R}^2 ; \| (x,y) – (0, 0) \| < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^2 ; \| (x,y) \| < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^2 ; \sqrt{x^2 +y^2} < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^2 ; x^2 +y^2 < 1 \right\}\\
\end{eqnarray*}

Já o conjunto de pontos que distam menos que 1 do ponto (1,0,1) está escrito abaixo:

\begin{eqnarray*}
B \left( (1,0,1) , 1 \right) & = & \left\{ (x,y,z) \in \mathbb{R}^3 ; \| (x,y,z) – (1,0, 1) \| < 1 \right\}\\
\\
& = & \left\{ (x,y,z) \in \mathbb{R}^3 ; \| (x-1,y,z-1) \| < 1 \right\}\\
\\
& = & \left\{ (x,y,z) \in \mathbb{R}^3 ; \sqrt{(x-1)^2 +y^2 + (z-1)^2} < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^3 ; (x-1)^2 +y^2+(z-1)^2 < 1 \right\}\\
\end{eqnarray*}

DEFINIÇÃO (Ponto de Acumulação)

Seja A \subset \mathbb{R} ^n. Um ponto P \in \mathbb{R} ^n é dito um ponto de acumulação de A se toda bola aberta com centro em P contiver uma infinidade de pontos de A.

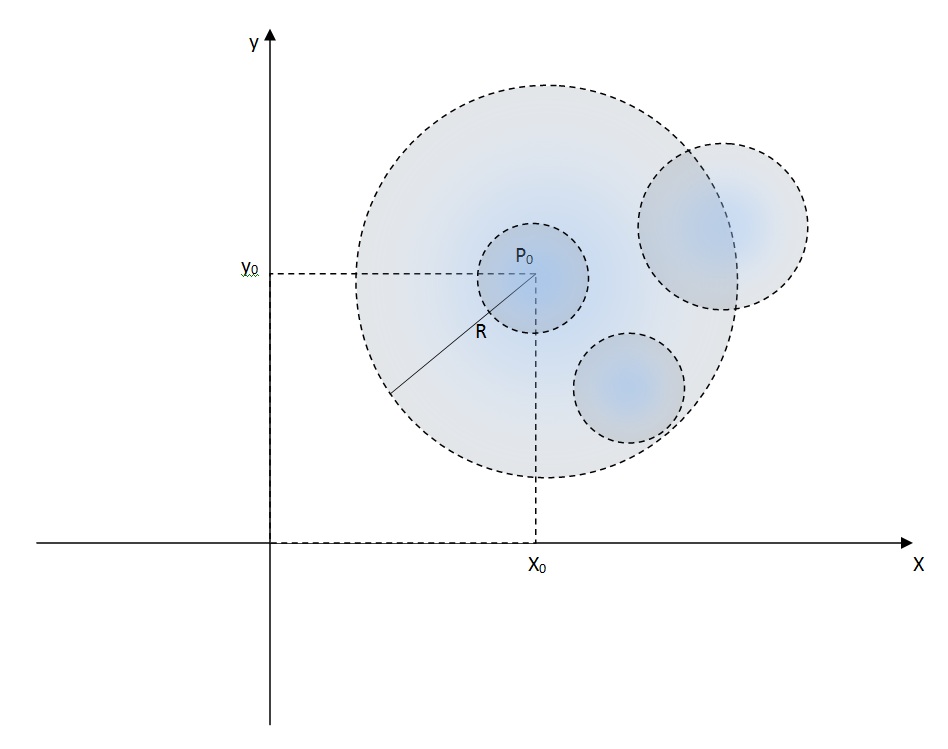
EXEMPLO

Seja A=\left\{ (x,y) \in \mathbb{R}^2; 0< \sqrt{(x-1)^2+(y-2)^2}\right\}<1.

Então,

• todos os pontos de A são pontos de acumulação de A.
• Os pontos da circunferência (x-1)^2+(y-2)^2 = 1 também não pertence a A, mas são pontos de acumulação de A.
• Qualquer ponto (x,y) do plano tal que (x-1)^2+(y-2)^2 > 1 não é ponto de acumulação de A.

A Definição de Limite

Abaixo vamos definir o limite de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.

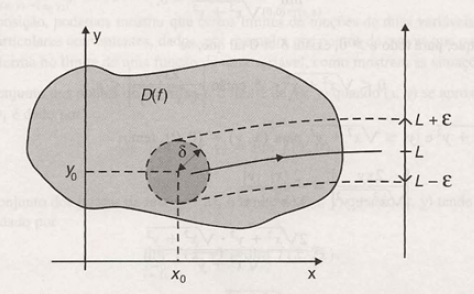
DEFINIÇÃO (Limite de Função de Várias Variáveis)

Sejam f:A \subset \mathbb{R} ^2 \rightarrow \mathbb{R} e (x_0, y_0) um ponto de acumulação de A. Dizemos que o limite de f(x,y), quando (x,y) se aproxima de (x_0, y_0) é um número real L se, para todo \varepsilon >0 existir um \delta >0 tal que | f(x,y) - L| < \varepsilon, sempre que \| (x,y) - (x_0,y_0) \| < \delta, para todo (x,y) \in A.

EXEMPLO

Considere f(x,y) = x.

Desta forma, $$\lim_{(x,y) \rightarrow (x_0,y_0)} f(x,y) = \lim_{(x,y) \rightarrow (x_0,y_0)} x = x_0.$$

Usando Curvas para Verificar a Existência do Limite

Em geral, para verificar a existência limites de funções de duas variáveis tomamos curvas particulares que passem em (x_0, y_0).

Nesse caso, o limite se transforma em um limite de uma função de uma variável.

Entretanto, precisamos tomar cuidado com curvas específicas, pois elas não preenchem todo o plano, sendo assim, consideramos a família de retas dadas por
\begin{eqnarray}
x(t) & = & \alpha t +x_0 \\
y(t) & = & \beta t +y_0.
\end{eqnarray}

Como veremos abaixo, em alguns casos, a parametrização desta família de retas deve ser ajustada para melhor se adequar ao problema.

Em geral, o mais indicado é usar as curvas de nível do gráfico da função.

Após substituir esta família de curvas no limite, se o resultado for um valor numérico, este será o valor do limite.

Se o resultado do limite depender dos parâmetros \alpha ou \beta, então o limite não existe.

Uma das grandes vantagens deste método é com ele transformamos um limite de uma função de várias variáveis num limite de uma função escalar.

Assim, todo o arsenal de técnicas do cálculo de limites para funções escalares está à nossa disposição, incluindo a Regra de L’Hospital.

EXEMPLO: 

Vamos calcular \lim_{(x,y) \rightarrow (0,0)}{\dfrac{2xy^2}{x^2 + y^4} } .

Este exemplo nos mostra que devemos ter cuidado ao usar curvas para calcular limites.

Note que se usarmos as retas como curvas genéricas chegaríamos à conclusão errada de que este limite existiria e seria zero.

Inspirado pelos expoentes das variáveis x e y no numerador e no denominador, e consequente pelas curvas de nível, iremos usar as parábolas como curvas genéricas para investigar este limite.

Parábolas genéricas que passem pela origem e tenham como eixo de simetria o eixo x são dadas por $$ x= \alpha t^2 $$ $$ y = \beta t. $$

Observe que $$\lim_{(x,y) \rightarrow (0,0)}{\frac{2xy^2}{x^2 + y^4} } = \lim_{t \rightarrow 0}{\frac{2 t^4 \alpha \beta ^2 }{\alpha ^2 t^4 + \beta ^4 t^4}}=$$ $$=\lim_{t \rightarrow 0}{\frac{2 \alpha \beta ^2 }{\alpha ^2 + \beta ^4 }} = \frac{2 \alpha \beta ^2 }{\alpha ^2 + \beta ^4 }.$$

Ou seja, este limite não existe!

EXEMPLO

A função f(x,y) = \dfrac{x^2 - y^2}{x^2 + y^2} tem limite em (0,0)? Justifique.

Neste caso, considere
\begin{eqnarray}
x(t) & = & \alpha t +0 \\
y(t) & = & \beta t +0.
\end{eqnarray}

e percebera que o limite não existe.

Propriedades do Limites

Se \lim_{(x,y) \rightarrow (x_0,y_0)}{f(x,y)} = L e \lim_{(x,y) \rightarrow (0,0)}{f(x,y)} = M, então

1. \lim_{(x,y) \rightarrow (x_0,y_0)}{\left( f(x,y) + g(x,y) \right)} = L+M;
2. \lim_{(x,y) \rightarrow (x_0,y_0)}{k. f(x,y)} =k L, (K constante);
3. \lim_{(x,y) \rightarrow (x_0,y_0)}{\left( f(x,y). g(x,y) \right)} = L.M;
4. \lim_{(x,y) \rightarrow (x_0,y_0)}{\left( \dfrac{f(x,y)}{g(x,y)} \right)} = \dfrac{L}{M}, se M \neq 0.
5. \lim_{(x,y) \rightarrow (x_0,y_0)}{[f(x,y)]^n} = L^n.
6. \lim_{(x,y) \rightarrow (x_0,y_0)}{\sqrt[n]{f(x,y)}} = \sqrt[n]{L}, se L \geq 0 e n é um inteiro, ou L \leq 0 e n é um inteiro ímpar.

EXEMPLO

Se (x,y) \rightarrow (x_0, y_0) e (x_0, y_0) é um ponto do domínio de f(x,y) , então o limite é igual à imagem da função neste ponto. Por exemplo, $$\lim_{(x,y) \rightarrow (0,2)}{ \sqrt{x+y}} = \sqrt{0+2} = \sqrt{2}.$$

EXEMPLO

$$\lim_{(x,y) \rightarrow (-1,1)}{ \dfrac{x^3y+4}{x+y-2}} = \dfrac{\lim_{(x,y) \rightarrow (-1,1)}{x^3y+4}}{\lim_{(x,y) \rightarrow (-1,1)}{x+y-2}} = – \dfrac{3}{2}$$

Teorema do Confronto

Se f(x,y) \leq g(x,y) \leq h(x,y) para 0 < \| (x,y) - (x_0,y_0) \| < \delta e se $$\lim_{(x,y) \rightarrow (0,0)}{f(x,y)} = L = \lim_{(x,y) \rightarrow (0,0)}{h(x,y)} $$ então $$\lim_{(x,y) \rightarrow (0,0)}{g(x,y)} = L.$$

Uma consequência direta do teorema do confronto acima enunciado é o resultado abaixo:

Se \lim_{(x,y) \rightarrow (0,0)}{f(x,y)}=0 e se |g(x,y)| \leq M, para 0 < \| (x,y) - (x_0,y_0) \| < \delta, onde \delta >0 e M>0 são reais fixos, então $$\lim_{(x,y) \rightarrow (0,0)}{f(x,y).g(x,y)} = 0$$

EXEMPLO

Calcule, caso exista \lim_{(x,y) \rightarrow (0,0)}{ \dfrac{x^3}{x^2+y^2}}.

Note que \dfrac{x^3}{x^2+y^2} = x.\underbrace{\dfrac{x^2}{x^2+y^2}}_{limitada}. Portanto, $$\lim_{(x,y) \rightarrow (0,0)}{ \dfrac{x^3}{x^2+y^2}} = \lim_{(x,y) \rightarrow (0,0)}{x \dfrac{x^2}{x^2+y^2}} = 0$$

Cálculo de Limites Envolvendo Indeterminações

Do limite de funções escalares temos as seguintes indeterminações:
$$ \frac{0}{0}, \quad +\infty-(+\infty), \quad -\infty-(-\infty), \quad \ 0\cdot\infty, \quad \frac{\infty}{\infty}, \quad \frac{0}{0}, \quad 1^{\infty}, \quad 0^0, \quad \infty^0. $$ Em geral, no limite de funções de várias variáveis nos concentramos na indeterminação \dfrac{0}{0}.

Além disso, as mesmas definições, resultados e estratégias usadas na solução dos limites, se estendem ao caso de três ou mais variáveis independentes, de maneira óbvia.

EXEMPLO

Calcule o limite abaixo: $$\lim_{(x,y) \rightarrow (2,1)}{ \dfrac{x^3+x^2y-2xy-2x^2 -2x +4}{xy+x-2y-2}}.$$

Temos que

\begin{eqnarray*}\lim_{(x,y) \rightarrow (2,1)}{ \dfrac{x^3+x^2y-2xy-2x^2 -2x +4}{xy+x-2y-2}} & = & \lim_{(x,y) \rightarrow (2,1)}{ \dfrac{x\left(x^2+xy-2 \right) -2 \left(x^2+xy-2 \right) }{(x-2)(y+1)}}\\
\\
& = & \lim_{(x,y) \rightarrow (2,1)}{ \dfrac{\left(x^2+xy-2 \right)(x-2) }{(x-2)(y+1)}}\\
\\
& = & \lim_{(x,y) \rightarrow (2,1)}{ \dfrac{x^2+xy-2}{y+1}}\\
\\
& = & \dfrac{4}{2}\\
\\
& = & 2
\end{eqnarray*}

EXEMPLO

\lim_{(x,y) \rightarrow (0^+,1^-)}{ \dfrac{x + y - 1}{\sqrt{x} -\sqrt{1-y}}}=?

Temos uma indeterminação \dfrac{0}{0}. Neste caso, costumamos fazer uma racionalização da seguinte forma.

$$\dfrac{x + y – 1}{\sqrt{x} -\sqrt{1-y}} = \dfrac{x + y – 1}{\sqrt{x} -\sqrt{1-y}}.1 =$$

$$= \dfrac{x + y – 1}{\sqrt{x} -\sqrt{1-y}}.\dfrac{\sqrt{x} + \sqrt{1-y}}{\sqrt{x} + \sqrt{1-y}}=$$

$$= \dfrac{(x + y – 1) (\sqrt{x} + \sqrt{1-y} )}{x + +y -1} = \sqrt{x} + \sqrt{1-y}$$

Daí,

\begin{eqnarray*}
\lim_{(x,y) \rightarrow (0^+,1^-)}{ \dfrac{x + y – 1}{\sqrt{x} -\sqrt{1-y}}}& = & \lim_{(x,y) \rightarrow (0^+,1^-)}{\sqrt{x} + \sqrt{1-y}}\\
& = & 0
\end{eqnarray*}

EXEMPLO

Queremos calcular o limite abaixo: $$\lim_{(x,y) \rightarrow (0, 0)}{\dfrac{2x}{(x^2+y^2)}\cos{\dfrac{1}{x^2+y^2}}}.$$

Observe que a função $$\cos{\dfrac{1}{x^2+y^2}}$$ é limitada entre -1 e 1.

Logo, se $$\lim_{(x,y) \rightarrow (0, 0)}{\dfrac{2x}{(x^2+y^2)}}$$ for igual a zero, podemos, pela consequência do Teorema do Confronto, dizer que

$$\lim_{(x,y) \rightarrow (0, 0)}{\dfrac{2x}{(x^2+y^2)}\cos{\dfrac{1}{x^2+y^2}}} = 0$$

Vamos então calcular $$\lim_{(x,y) \rightarrow (0, 0)}{\dfrac{2x}{(x^2+y^2)}}.$$

Usando a substituição as curvas C(t) = (t,0) e D(t) = (0,t), obtemos que dois valores diferentes para esse limite. Logo, o limite \lim_{(x,y) \rightarrow (0, 0)}{\dfrac{2x}{(x^2+y^2)}} não existe.

Por consequência, $$\lim_{(x,y) \rightarrow (0, 0)}{\dfrac{2x}{(x^2+y^2)}\cos{\dfrac{1}{x^2+y^2}}}$$ não existe!

EXEMPLO

Calcule o limite $$\lim_{(x,y) \rightarrow (0, 0)}{e^{x/y}}.$$

Neste caso, considere
\begin{eqnarray}
x(t) & = & \alpha t +0 \\
y(t) & = & \beta t +0.
\end{eqnarray}

Assim, quando t tende a zero, (x,y) tende a (0,0).

Desta forma,

$$\lim_{(x,y) \rightarrow (0, 0)}{e^{x/y}} = \lim_{t \rightarrow 0}{e^{\frac{\alpha t }{\beta t}}}=$$

$$=\lim_{t \rightarrow 0}{e^{\frac{\alpha}{\beta}}} = e^{\frac{\alpha}{\beta}}.$$

Logo, o limite não existe!

Limite de Funções de Várias Variáveis | Listas de Exercícios Resolvidos

• Limite de Funções de Várias Variáveis | 1ª Lista de Exercícios Resolvidos
• Limite de Funções de Várias Variáveis | 2ª Lista de Exercícios Resolvidos

Leia Mais:

• Continuidade de Funções de Várias Variáveis
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
• Funções de Várias Variáveis Reais a Valores Reais ou Campos Escalares
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula

Assista Nossa Vídeo-Aula Sobre Limites de Funções de Várias Variáveis