Modelo SIS de Propagação de Infecção | Matemática Aplicada à Epidemiologia

Um modelo em epidemiologia é uma forma simplificada de descrever a transmissão de doenças transmissíveis através de indivíduos. Neste artigo queremos falar sobre o Modelo SIS, par amodelar a propagação de infecções.

As infecções são situações bem cotidianas na vida de toda a população, elas são causadas por agentes externos podendo ser vírus, bactérias, parasitas e até mesmo fungos. Elas têm sido responsáveis por enorme sofrimento e morte ao longo da história, assim como foi a peste bubônica, infecção que matou pelo menos um terço da população europeia da época.

Atualmente, após termos passado por uma pandemia mundial muito se pergunta em como calcular a propagação de uma infecção, já que sabendo esse dado previamente os meios para se prevenir e combater se tornam viáveis e ajudam se preparar para o que pode vir.

E é isso que vamos estudar nesse trabalho, iremos falar matematicamente como ocorre uma propagação infecciosa através das E.D.O.’S (equações diferenciais ordinárias). Utilizamos essas equações pois “Os modelos de EDO são os mais utilizados para antecipar a propagação destas doenças e para explorar o efeito provável das contra medidas” [1].

O modelo que iremos utilizar para calcular essa propagação é o modelo SIS, onde defende que infecções como a covid-19 se espalha devido a combinação de características patogênicas e de relação humana. As características patogênicas determinam como uma pessoa contaminada pode infectar a outra, já o comportamento humano determina com que frequência essa contaminação pode acontecer.

Fundamentação teórica do problema de propagação de infecção

Nesse trabalho vamos considerar uma doença infecciosa para a qual ninguém tem, nem ganha imunidade. Assim, um indivíduo suscetível pode contrair a doença de um indivíduo infectado. O indivíduo suscetível, então, torna-se infectado, e mantém-se infectado até ficar curado. Uma vez curado, o infectado volta a ser suscetível, dado que não existe imunidade a esta doença.

Se S(t) é a fração da população que é suscetível o instante t e seja l(t) a fração da população que está infectada no instante t , assim temos que $$ S(t) \geq 1, \qquad l(t) \geq 0 \qquad e \qquad S(t)+l(t) = 1.$$

Um indivíduo suscetível se torna infeccioso após um contato com um indivíduo infeccioso, esse contato pode ser caracterizado como convívios, saliva, espirros etc.

Se multiplicarmos S(t) e l(t) por uma constante k e então multiplicamos também a taxa com que os contatos ocorrem por k significa que a taxa em que a doença é transmitida em t é proporcional ao produto S(t) \times l(t).

Deste modo podemos supor que o tempo t  em que a taxa dos infectados voltem a ser suscetíveis é proporcional a l(t) . Assim, chegamos as seguintes equações para as taxas $$ \frac{dS}{dt} = -\beta S(t)+\gamma l(t) \qquad (1.1)$$ $$ \frac{dl}{dt} = \beta S(t)-\gamma l(t) \qquad (1.2)$$ onde \beta e \gamma são constantes de proporciaonalidade positivas e daremos mais ênfase nelas abaixo.

Frequentemente iremos usar um ponto para representar a derivada em relação a t . Assim, as equações 1.1 e 1.2 podem ser reescritas como $$ \dot{S} = -\beta S(t)l(t)+ \gamma l(t) \qquad (1.3) $$ $$ \dot{l} = \beta S(t)l(t) – \gamma l(t) \qquad (1.4) $$ que simplificadas podemos usar ainda a equação mais simples dada por $$ \dot{S} = -\beta S l + \gamma l \qquad (1.5) $$ $$ \dot{l} = \beta S l – \gamma l \qquad (1.6)$$ que são, de fato, as equações que constituem o modelo SIS de propagação de infecção.

Somando as duas equações (1.5) e (1.6) temos que $$ \dot{S}+\dot{l} = 1,$$ então S + l permanece igual a 1 para sempre, afinal S e l são frações da população.

Contudo, as equações não nos dizem o que ocorre ao longo do tempo. Não sabemos se a doença irá desaparecer, ou espalhar-se até a população inteira ficar infectada, ou oscilar continuamente, ou tender para um valor intermédio ficando presente na população para sempre. As equações (1.5) e (1.6) constituem um sistema de equações diferenciais. As soluções do sistema irão nos dizer o que acontece.

Modelagem do problema de propagação de infecção

No sistema SIS, vimos que S(t)+l(t)=1 para qualquer tempo em t . Então, realmente não necessitamos das duas equações, dado que conseguimos encontrar S(t)=1-l(t) , podemos a partir da equação (1.5) temos $$ \dot{l} = \beta (1-l)l – \gamma l = ( \beta – \gamma )l – \beta l^2 . \qquad (1.7).$$

Podemos encontrar a solução geral usando separação de variáveis e integração de frações racionais. Iremos fazer isso para valores de \beta e \gamma . Uma forma de ver isso mais facilmente é desenhando uma linha de fase, eixo  com pontos onde se encontram equilíbrios e setas mostrando onde as soluções crescem e decrescem onde

1) \dot{l} > 0 , l(t) é crescente;

2) \dot{l} < 0 , l(t) é decrescente;

3) \dot{l} = 0 , existe um equilíbrio.

O que pode ajudar a visualizar essas situações é desenhando um gráfico através da função $$ \dot{l} = ( \beta – \gamma )l – \beta l^2  = l( \beta – \gamma – \beta l ) \qquad (1.8).$$

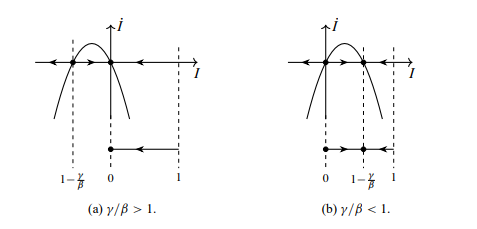
A parábola acima é usada para desenhar a linha de fase, onde as setas para a esquerda representam \dot{l} = l < 0 e setas para a direita representam \dot{l} = l > 0. Então nós restringimos ao intervalo L para obter o retrato de fase:

1) Se \dfrac{\gamma}{\beta} > 1 todas as soluções em L tendem a zero quando t \rightarrow \infty ;

2) Se \dfrac{\gamma}{\beta} < 1 todas as soluções em L com l(0) > 0 tendem a 1 - \dfrac{\gamma}{\beta} quando t \rightarrow \infty . Por outro lado, quando t \rightarrow \infty ; as soluções com 0 < l(0) < 1 - \dfrac{\gamma}{\beta}   tendem a zero.

Já as interpretações dos retratos de fase são as seguintes:

1) Para \dfrac{\gamma}{\beta} > 1 se a doença entra na população, ela desaparece;

2) Para \dfrac{\gamma}{\beta} < 1 , se a doença entra na população, a fração da população com a doença tende para o número positivo l = 1 - \dfrac{\gamma}{\beta} e, por fim, prevalece na população com esse valor (grosso modo).

Nesse segundo caso, a doença é dita endêmica e o equilíbrio l = 1 - \dfrac{\gamma}{\beta} é chamado equilíbrio endêmico. Em geral, não consideramos \gamma = 0 ; admitimos que \gamma > 0 . No caso \gamma = 0 corresponderia a uma doença para qual não há forma de se recuperar. Neste caso temos que l(t) \rightarrow 1.

No caso \dfrac{\gamma}{\beta} > 1 as soluções levam um tempo infinito a aproximarem-se de zero. Porém na realidade o tamanho da população é finito, então assim que a fração da população é suficientemente pequena, não existem mais infectados. Esta é a razão pelo qual podemos dizer que a doença desaparece.

Os epidemiologistas não distinguem o caso usando a fração \dfrac{\gamma}{\beta} como fizemos. Ao invés disso, eles usam a fração \dfrac{\beta}{\gamma} , dizendo que se for \dfrac{\gamma}{\beta} < 1 a doença desaparece e se for \dfrac{\gamma}{\beta} > 1 a doença é endêmica.

Solução do problema de propagação de infecção pelo modelo SIS

Para solucionarmos e contextualizarmos os problemas citamos anteriormente precisamos definir as constantes \beta e \gamma, e o porquê epidemiologistas as preferem.

A Constante Beta (O Coeficiente de Transmissão)

Vamos olhar para a dimensão real da população ao invés de frações populacionais. Lembrando que estamos considerando a população com tamanho constante, ignoramos mortes, nascimentos, imigração e emigração. Seja N o tamanho da população, s(t) o número de suscetíveis e i(t) o número de infectados. Deste modo s(t) + i(t) = N .

A doença se propaga devido aos contatos com características apropriadas para a transmissão da doença no qual chamamos apenas de contatos. Supomos que a taxa de contato por pessoa infectada é constante. Então, supondo uma população homogeneamente misturada e multiplicando por \dfrac{s(t)}{N} , obtemos a taxa de indivíduos suscetíveis contatados por pessoa contaminada.

Se o tempo for medido em dias, temos:  $$ \frac{ \text{pessoas contadas} }{ text{pessoa infectada} \times \text{dia} } \times \frac{s(t)}{N} = \frac{ \text{pessoas suscetíveis contadas} }{ \text{pessoa infectada} \times \text{dia} } \qquad (1.9) $$ Multiplicando a taxa anterior pela probabilidade de cada pessoa suscetível de contrair a doença devido ao contato, obtemos a taxa de novas pessoas infectadas por pessoa infectada $$ \frac{ \text{Novas pessoas infectadas} }{ \text{pessoa infectada} \times \text{dia} }  = \\ = \frac{ \text{pessoas contadas} }{ \text{pessoa infectada} \times \text{dia} } \times \frac{s(t)}{N} \times \text{probabilidade de transmissão} \qquad (1.10) $$ Assim, definimos $$ \beta = \frac{\text{pessoas contadas} }{ \text{pessoa infectada} \times \text{dia} } \times \text{probabilidade de transmissão} \qquad (1.11) .$$

Usamos o símbolo \beta pois tem o mesmo significado que o \beta que usamos no sistema (1.5) e (1.6). Na epidemiologia matemática, a constante \beta é chamada de coeficiente de transmissão, sendo a taxa de novas infecções quando todas as pessoas contatadas são suscetíveis (s(t) = N) como ocorre no início de uma epidemia. A constante \beta também pode ser chamada de taxa de contatos adequados por infectados.

Por definição \beta é a multiplicação de dois termos. O primeiro termo é em condições normais onde as pessoas não estão usando meios para se protegerem de uma doença, como máscaras etc.; o segundo termo é a probabilidade de transmissão que é uma característica da própria doença, ou seja, a quão contagiosa ela é. O primeiro, no entanto, depende do estilo de vida da população.

Uma vez que i(t) é o número de infectados no instante t , a taxa de novas infecções na população inteira, no momento t , é obtida multiplicando a equação (1.10) por i(t) $$ \frac{ \text{novas pessoas infectadas} }{ \text{dia} } = \beta \times \frac{s(t)}{N} \times i(t) \qquad (1.12).$$

A taxa que os infectados se recuperam é proporcional a i(t) , com a mesma constante de proporcionalidade \gamma utilizada anteriormente. Assim obtemos o sistema de equações diferenciais $$ \frac{dS}{dt} = – \frac{\beta}{N} s i +  +\gamma i \qquad (1.13)$$ $$ \frac{di}{dt} = \frac{\beta}{N} s i -\gamma i \qquad (1.14).$$

Se o tempo for medido em dias, então as unidades de ds/dt são pessoa/dia. Dado que N , s e i tem unidades de pessoas, então  deve ser 1/dia . Isso porque  representa o número de pessoas contatadas por pessoa infectada por dia, ou o número de novas infecções causadas por dia por cada infectado quando toda a população é suscetível. A unidade pessoa é cancelada.

A Constante Gama

Por simplicidade vamos supor que a população inteira está infectada no instante 0 e que não há reinfecções, assim o fenômeno de recuperação é isolado. Então a partir da equação (1.6) e simplificando para o valor do problema inicial temos que a solução é $$ I(t) = e^{- \gamma t } \qquad (1.15).$$

A taxa qual I varia é \dot{I}=-\gamma e^{- \gamma t}, sendo negativa dado que   I(t) decresce com a cura das pessoas. Por outro lado, a taxa a qual as pessoas se curam é - \dot{I}=\gamma e^{- \gamma t}, sendo positiva. Por fim, quando todos se curarem a equação será a seguinte $$ \int\limits_{0}^{\infty}{- \dot{I} dt} = \int\limits_{0}^{\infty}{\gamma e^{- \gamma t} dt} = 1. \qquad (1.16)$$

Como as pessoas que ficam curadas no instante t estiveram doentes durante um tempo t , o tempo médio para qual as pessoas estão doentes é o valor médio de t no intervalo 0 \leq t ˂ \infty . Este valor médio é $$\int\limits_{0}^{\infty}{- t\dot{I} dt} = \int\limits_{0}^{\infty}{\gamma t e^{- \gamma t} dt} = \frac{1}{\gamma} \qquad (1.17)$$

Assim temos que \dfrac{1}{\gamma} é o tempo médio para qual as pessoas ficam doentes com a doença que está sendo modelada. Note que as unidades para \dfrac{1}{\gamma}  são 1/dia, assim como na seção acima.

Conclusão

A suposição que a infecção se alastra a uma taxa proporcional ao produto entre as frações das populações de infectados e suscetíveis é chamada de lei de ação das massas, que vem da química, onde fala que em uma solução com que contém dois reagentes a taxa de de reação é proporcional ao produto das concentrações (quando bem agitados). Em epidemiologia, uma analogia a uma solução bem agitados é uma população bem misturada, se encontrando aleatoriamente.

Uma equação diferencial como o modelo SIS, pode enganar no início de uma pandemia. Já que o modelo SIS prevê que basta um individuo contrair a doença infecciosa para que esta se alastre até que atinja o equilíbrio endêmico. Porém, a um certo grau de aleatoriedade envolvido na possibilidade de um só individuo infectado efetivamente conseguir infectar alguém e, se sim, quantas pessoas.

Segundo o estatístico George Box “todos os modelos estão errados, porém alguns são úteis.” As extensões do modelo SIS estão seguramente errados, mas são definitivamente úteis já que, eles têm sido muito usados por governos durante a pandemia de Covid-19 para prever o progresso da epidemia no caso de serem aplicados políticas governamentais.

Referências Bibliográficas:

1. LÓPEZ-FLORES, Marlon M.; MARCHESIN, Dan; MATOS, Vitor; SCHECTER; Stephen. Equações diferenciais e modelos epidemiológicos. Rio de Janeiro, Brasil. Impa; julho de 2021.
2. SILVA, Daniel Neves. “Peste negra”; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/historiag/pandemia-de-peste-negra-seculo-xiv.htm

Leia Mais sobre Matemática Aplicada:

• Criptomoedas | Qual é a matemática da criptografia do Bitcoin?
• Equação do Jogador: Conheça a matemática da aposta esportiva
• Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
• Dinâmica populacional e função logística | Matemática aplicada à ecologia
• Efeito Borboleta | Edward Lorenz e a Teoria do Caos
• Mileva Maric | A Coautora da Teoria da Relatividade Especial?
• É impossível Pensar o Universo Sem A Matemática?