Dinâmica populacional e função logística | Matemática aplicada à ecologia

Neste artigo apresentamos um estudo introdutório da dinâmica populacional como aplicação das E.D.O.’s de 1ª ordem, apresentado o modelo de Malthus, a função logística de Verhulst e as curvas de Gompertz.

A dinâmica populacional foi a primeira investida dos ecologistas na tentativa de formular e resolver seu problemas por raciocínio matemático, e talvez tenha se tornado a aplicação matemática mais importante neste ramo: entender como populações crescem e decrescem. Para tal objetivo as equações diferenciais ordinárias de primeira ordem são uma ferramenta crucial.

Num primeiro momento pode parecer impossível modelar o crescimento de espécies usando equações diferenciais, pois a população de cada espécie se altera por quantidades dadas em números inteiros, ou seja, esta população não pode ser derivada em função do tempo. Por outro lado, se uma dada população é muito grande e repentinamente é acrescida de mais um elemento, então a alteração é muito pequena se comparada com toda a população. Assim, nós fazemos a aproximação de que grandes populações se alteram continuamente e, portanto, são diferenciáveis em relação ao tempo.

Neste sentido, os modelos mais utilizados são aqueles que interpretam o crescimento populacional partindo da suposição de que a taxa de crescimento da população depende do seu tamanho. Assim, se P representa a população num instante t , então todos os modelos possuem a forma $$ \frac{dP}{dt} = f(P),$$ em que f é alguma função da quantidade de habitantes de P .

Crescimento Populacional Exponencial e o Modelo de Malthus

O problema de valor inicial $$\frac{dx}{dt} = kx, \qquad x(t_0) = x_0 , $$ onde k é uma constante de proporcionalidade (que pode ser positiva ou negativa), ocorre em muitas teorias físicas envolvendo crescimento e decrescimento. Outras aplicações desta equação estão na física (decaimento radioativo) e na química (reações), mas serão exploradas em outros artigos. É interessante observar que o estudo de substâncias que se desintegram pela radioatividade levou à descoberta da cronologia do carbono, que é um meio de datar fósseis ou mesmo uma múmia.

A equação $$\frac{dx}{dt} = kx, \qquad x(t_0) = x_0 , $$ pode ser resolvida como um E.D.O. de primeira ordem separável. Desta forma, $$ \frac{dx}{x} = k dt \Leftrightarrow \ln{|x|} = kt + c \Leftrightarrow $$ $$ \Leftrightarrow x(t) = ce^{kt}.$$ Logo, usando a condição inicial encontramos como solução deste problema $$ x(t) = x_0 e^{k(t – t_0 )} .$$ Esta solução nos diz que se k > 0 então a função modela um crescimento sem assíntotas, ou seja, a população cresce indefinidamente. Por outro lado, se k < 0 , o decrescimento tenderá a zero.

Além disso, qualquer fenômeno que tenha como modelo a equação diferencial $$\frac{dx}{dt} = kx, \qquad x(t_0) = x_0 , $$ possui crescimento ( k > 0 ) ou decrescimento ( k < 0 ) exponencial.

O MODELO DE MALTHUS

A figura central no início da teoria matemática do crescimento populacional é o inglês Thomas Robert Malthus (1766 – 1834), um matemático graduado em Cambridge, que ordenou-se pastor da Igreja da Inglaterra e foi professor de história e economia política. Em seu famoso trabalho “An Essay on the Principle of Population”, ele argumentou que a população crescia em proporção constante do número inicial, num modelo similar àquele desenvolvido anteriormente, onde a constante de proporcionalidade era positiva.

Isto é, na visão de Malthus, o modelo populacional a ser utilizado para medir o população mundial obedecia à equação $$\frac{dP}{dt} = kP, \qquad P(t_0) = P_0 , $$ que, como já vimos possui crescimento ( k > 0 ) exponencial.

Uma característica do crescimento exponencial é o tempo de duplicação da constante: leva exatamente a mesma quantidade de tempo para a população se duplicar partindo da quantidade inicial, independente de qual seja a população inicial. Isso quer dizer que pelo modelo de Mathus, a população cresceria infinitamente numa progressão geométrica. No caso da população humana ele calculou que o tempo de duplicação seria de 25 anos.

Com isso Malthus tinha matematicamente um raciocínio perfeito para sua tese de que o controle de natalidade fosse adotado no mundo, pois em seu ensaio ele deixou evidente seu pessimismo quanto ao desenvolvimento humano. Ele acreditava que a pobreza fazia parte do destino da humanidade, baseado na premissa de que a população possuía potencial de crescimento ilimitado, ao contrário da produção de alimentos.

Para conter o ritmo acelerado do crescimento populacional, Malthus, pautado na sua formação religiosa, acreditava na necessidade de um controle de natalidade, que chamou de “controle moral”. Esse controle não deveria ser feito pelo uso de métodos contraceptivos, mas pela abstinência sexual ou adiamento de casamentos. Vale ressaltar que esse controle foi sugerido apenas para a população mais pobre. Segundo ele, era necessário forçar a população mais carente a diminuir o número de filhos.

Porém, logo os estudiosos perceberam que o modelo de Malthus não era realístico para modelar o crescimento populacional humano. Ele pode até funcionar para o inferir o crescimento populacional humano em um curto espaço de tempo, mas para décadas ele se torna falho por uma observação bem simples: Malthus não incorpora em sua equação efeitos inibidores do crescimento, como guerras e epidemias, por exemplo.

O modelo de Malthus quando confrontado com os dados reais dos censos de países desenvolvidos mostra uma discrepância crescente exponencialmente, com erros cada vez maiores. Na comparação com a população dos Estados Unidos, por exemplo, em um século, de 1790 a 1890, seu modelo tinha um erro de 20% na população aferida pelo censo. Isso se dá porque o modelo malthusiano não previa as mortes da Guerra Civil, por exemplo. Com isso, percebeu-se a necessidade de melhorar este modelo, algo que seria feito pelo belga Pierre-Francois Verhulst (1804 – 1849).

A Função Logística de Verhulst

A modelagem realizada anteriormente por Malthus, como vimos, funciona em espaços curtos de tempo. Entretanto, em muitas circunstâncias, esta equação diferencial não se aplica, pois os dados coletados diferem grosseiramente do que é previsto pela equação. Por volta de 1840, o matemático-biólogo P. F. Verhulst preocupou-se com as formulações matemáticas para previsão de populações humanas de vários países.

Uma das equações estudadas por ele foi $$ \frac{dP}{dt} = P(a-bP)$$ onde a e b são constantes positivas. Esta equação ficou conhecida como a equação logística e sua solução é chamada de função logística (seu gráfico é referenciado como curva logística).

Os coeficientes a e b são chamados de coeficientes vitais da população. Para aplicar os resultados da solução da equação logística ao crescimento populacional dos seres humanos, nós devemos estimar estes coeficientes que governam a equação. Alguns ecologistas calculam que o valor natural de a seria 0,029.

Com cálculos simples, e sabendo que a população crescia a uma taxa de 2% ao ano quando era de apenas (3,34) \times 10^{9} (este seria o valor inicial da equação), podemos inferir pelo método logístico que a população da Terra tenderia ao valor limite de 10,76 bilhões de pessoas. Obviamente, os desenvolvimentos tecnológicos, considerações sobre poluição, epidemias e atritos sociais têm significativa influência nos coeficientes vitais, portanto eles deve ser recalculados ano após ano.

A diferença da equação de Verhulst é que ela incorpora a subtração da taxa média de nascimento pela taxa média de óbito, além de considerar condições de deterioração inerentes ao crescimento populacional, como poluição, competição por alimento e energia, que são efeitos inibidores do crescimento: $$ \frac{dP}{dt} = \left[ \text{ taxa média de crescimento} \right] – \left[ \text{ taxa média de óbito} \right]  = P(a-bP).$$

Até por isso, as curvas logísticas são modelos bem acurados para a previsão de crescimento populacional, em um espaço limitado, de certos tipos de bactérias, protozoários, pulgas e moscas de frutas. Sociólogos e mesmo analistas financeiros têm usado o modelo de Verhulst para estudar a propagação de informações e o impacto de anúncios em centros populacionais.

Embora Verhulst tenha tentado testar seu modelo em populações reais, frustrou-se com as informações impressas dos censos disponíveis na década de 1840, quando empreendeu seus estudos. Como os dados populacionais existentes na época eram inadequados para formar um teste efetivo do modelo logístico, o trabalho de Verhulst ficou esquecido por aproximadamente 80 anos. Foi redescoberto independentemente por dois cientistas norte-americanos que trabalhavam na Universidade John Hopkin, Raymond Pearl e Lowell J. Reed.

Em 1920, Pearl e Reed examinaram a proximidade da curva de crescimento populacional dos Estados Unidos com a curva logística. Usando dados dos censos de 1790, 1850 e 1910 para encontrar valores dos parâmetros da solução da equação logística eles perceberam que o modelo logístico oferecia um excelente retrato das variações populacionais dos Estados Unidos de 1790 a 1950.

Mesmo assim, é importante lembrar que as previsões da função logística não funcionam muito bem para modelar populações do passado. Em seu livro “Equações Diferenciais e Suas Aplicações”, Martin Braun ofereceu uma interessante observação: “Um aluno meu sugeriu que usássemos esta equação para encontrar o valor de t em que p(t) =2 , e assim deduzir quanto tempo atrás a humanidade surgiu na Terra. Superficialmente, esta parece ser uma ideia fantástica. Porém, nós não podemos viajar tão longe no passado, uma vez que nosso modelo é não tão confiável quando as população é muito pequena”. 

A SOLUÇÃO DA EQUAÇÃO EQUAÇÃO LOGÍSTICA DE VERHULST

A solução da equação logística de Verhulst é encontrada através do método da separação das variáveis. Usando frações parciais podemos escrever: $$ \frac{dP}{P(a-bP)} = dt $$ $$\left[ \frac{1/a}{P} + \frac{b/a}{a-bP} \right]dP = dt $$ $$\frac{1}{a} \ln{|P|} – \frac{1}{a}\ln{|a-bP|} = t +C $$ $$ \ln{ \left| \frac{P}{a-bP} \right| } = at+aC$$ $$ \left| \frac{P}{a-bP} \right| = c_1 e^{at} $$ Isolando P(t) nesta solução implícita encontramos $$P(t) = \frac{a c_1 }{bc_1 + e^{-at} }$$

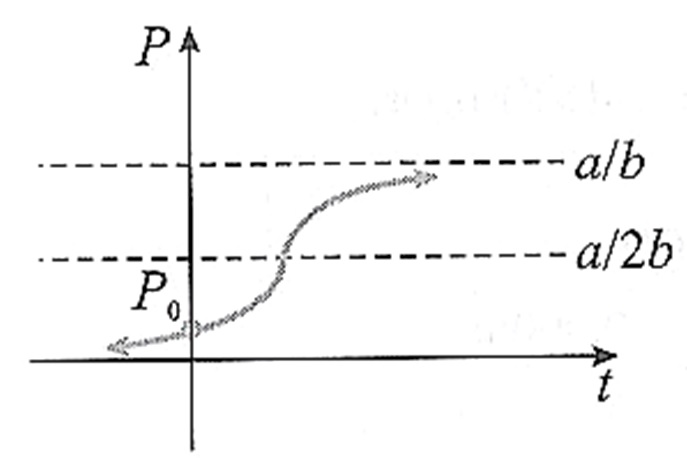
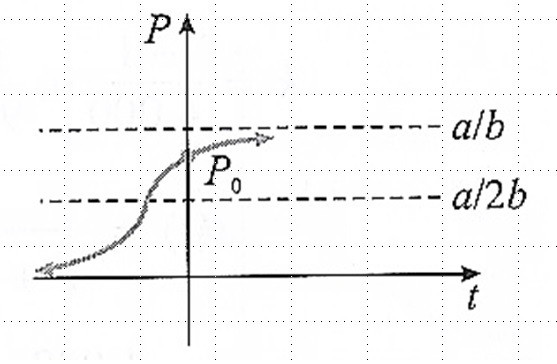
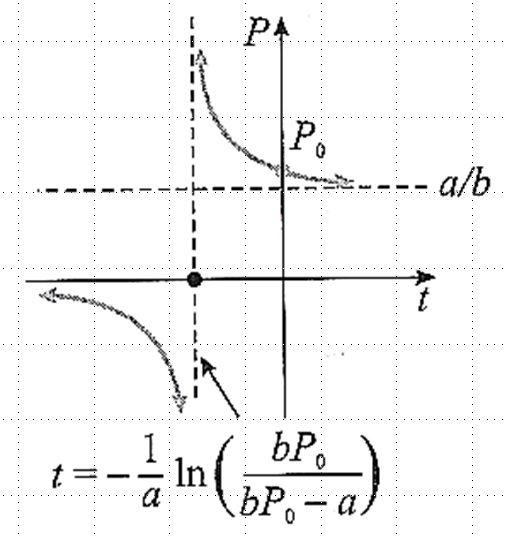
Se a condição inicial é dada por P(0) = P_0 , onde P_0 \neq a/b , podemos encontrar c_1 = \dfrac{P_0}{a-bP_0} . Assim,  como esta equação modela o crescimento populacional ao longo do tempo t , devemos investigar o que acontece com esta função quando o tempo cresce indefinidamente: $$P(t) = \frac{a P_0 }{bP_0 + (a-bP_0)e^{-at} }$$ Observe que $$ \lim\limits_{ t \rightarrow + \infty }{P(t) } = \frac{a}{b}.$$ Ou seja, o gráfico desta solução possuirá uma assíntota horizontal em P = a/b .

Abaixo temos três gráficos da função logística de Verhulst. Onde mostramos como os pontos de inflexão mudam de acordo com com os valores da condição inicial P(0) = P_0

As Curvas de Gompertz

Uma modificação da equação logística é $$ \frac{dP}{dt} = P(a-b\ln{(P)}),$$ em que a e b são constantes. Usando novamente a separação de variáveis podemos encontrar uma solução dada por $$P(t) = e^{a/b}e^{-ce^{-bt}},$$ em que c é uma constante arbitrária.

Observe que se b>0 , então $$\lim\limits_{t \rightarrow + \infty}{P(t)} = e^{a/b},$$ enquanto que, caso contrário, se b<0 e c>0 então $$\lim\limits_{t \rightarrow + \infty}{P(t)} = 0.$$ O gráfico desta função é chamado de curva de Gompertz e é muito semelhante ao gráfico da função logística. Estas funções são encontradas nos estudos de crescimento ou decrescimento de certas populações, no crescimento de tumores, em previsões atuariais (estudo dos riscos, expectativas e previsões financeiras) e no estudo de crescimento de renda na venda de um produto comercial.

Abaixo, temos duas possibilidades para o gráfico de P(t) .

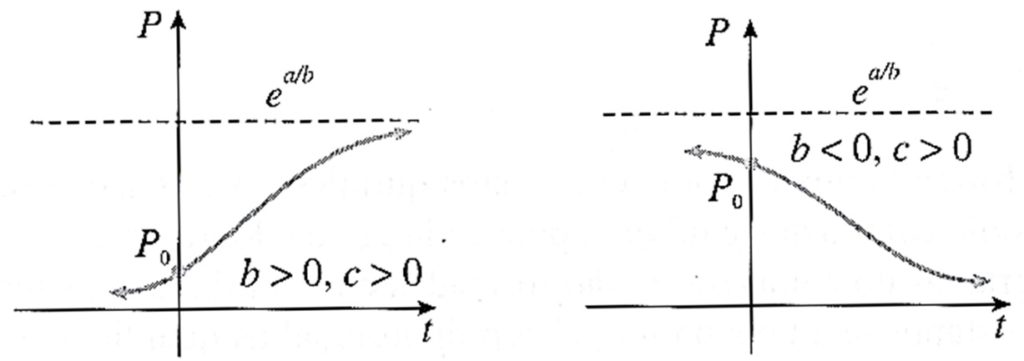
Devemos observar que o modelo de Gompertz pode ser também visto como uma generalização do modelo exponencial de Malthus.

Conclusão

Para encontrar modelos mais acurados de crescimento populacional, nós não devemos considerar a população como feita de um grupo homogêneo de indivíduos. Em vez disso, devemos subdividir a população em diferentes grupos etários. Devemos também subdividir a população entre homens e mulheres, uma vez que a taxa de reprodução geralmente depende mais do número de mulheres do que do número de homens.

Modelos mais acurados de crescimento populacional podem ser obtidos refinando o modelo logístico de várias maneiras diferentes. Fatores adicionais podem ser acrescidos à equação diferencial para incorporar o conceito de que a taxa de variação da população é uma função não só da população, mas também do tempo, ou seja, a equação pode ser reescrita como $$ \frac{dP}{dt} = f(P,t).$$

Talvez, a maior crítica ao modelo logístico para o crescimento populacional é que algumas populações tem sido observadas como flutuantes periodicamente entre dois valores, e todo tipo de flutuação são pontos fora da curva logística. Por outro lado, algumas destas flutuações podem ser explicadas pelo fato de que quando certas populações alcançam uma densidade suficientemente grande, elas se tornam suscetíveis a epidemias. A epidemia traz a população para um número mais baixo, de onde começa novamente a crescer até ponto onde esteja grande o bastante para que outra epidemia ataque novamente.

Demógrafos usam cada vez mais sofisticados e complexos modelos matemáticos de caráter determinístico e probabilístico para estudar variações no crescimento populacional no passado e fazer projeções sobre o futuro. Embora haja muitas abordagens diferentes para a criação de tais modelos, na maioria das vezes são extensões ou generalizações  de uma equação diferencial não-linear de primeira ordem.

Leia Mais:

• Equações Diferenciais Ordinárias de 1ª Ordem Separáveis.
• EDOs de 1ª Ordem | 1ª Lista Exercícios Resolvidos
• EDO’s de 1ª Ordem Separáveis | 1ª Lista de Exercícios Resolvidos
• É impossível Pensar o Universo Sem A Matemática?

Referências Bibliográficas:

1. “Advanced Engineering Mathematics”. KREYSZIG, E. .
2. “Equações Diferenciais: Volume 1” – Dennis G. Zill e Michael R. Cullen
3. “Dinâmica Populacional”, Michael Olinick.
4. “Equações Diferenciais e Suas Aplicações”. Martin Braun.

[blog_subscription_form]