Hipérbole (Seções Cônicas) | 9 Exercícios Resolvidos com Soluções Detalhadas

Melhore sua compreensão de hipérboles como curvas planas geradas por seções cônicas com estes 9 exercícios resolvidos com soluções detalhadas. Perfeito para estudantes de graduação em ciências exatas e da terra.

Se você está procurando melhorar sua compreensão das hipérboles como curvas planas geradas por seções cônicas, você veio ao lugar certo. Neste artigo, forneceremos 9 exercícios resolvidos com soluções detalhadas para ajudá-lo a dominar esse importante conceito da geometria Analítica. Seja você um estudante de graduação em ciências exatas e da terra, esses exercícios irão ajudá-lo a aprimorar suas habilidades e aprofundar sua compreensão das hipérboles como seções cônicas.

O que é uma hipérbole como curva plana gerada por seção cônica?

Sejam duas retas e e r concorrentes em O e não perpendiculares. Conservemos fixa a reta e e façamos girar 360º em torno de e mantendo constante o ângulo entre estas retas. Nestas condições, a reta r gera uma superfície cônica circular infinita formada por duas folhas separadas pelo vértice O .

Especificamente, uma hipérbole é formada quando um plano intercepta as duas metades de um cone duplo em um ângulo que é mais acentuado que o ângulo dos lados do cone. Isso resulta em uma curva que tem duas ramificações que são imagens espelhadas uma da outra e que nunca se cruzam. A forma de uma hipérbole é semelhante à de uma parábola, mas com duas ramificações em vez de uma.

Ou seja, quando uma superfície cônica é seccionada por plano \pi qualquer que não passa pelo vértice O , a seção cônica será uma hipérbole se \pi for paralelo ao eixo e ;

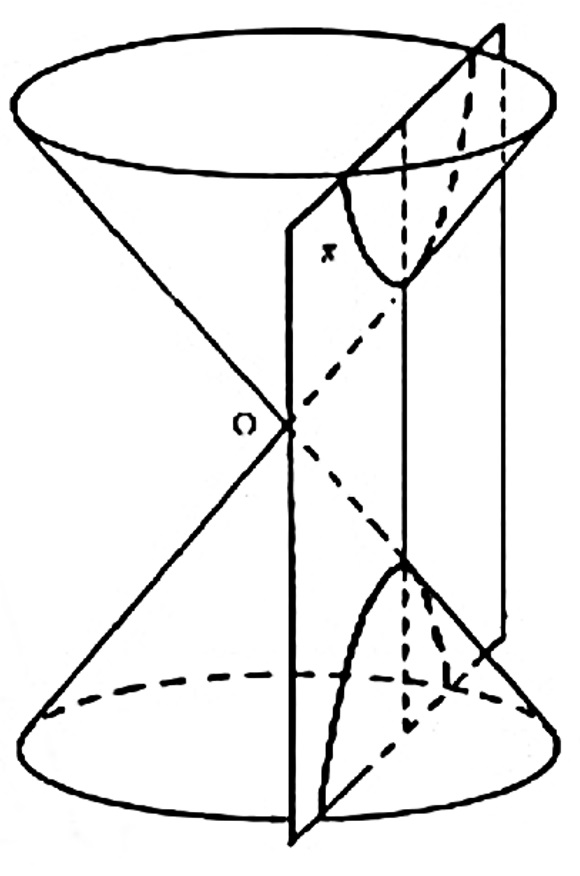
Construindo uma Hipérbole no Plano

A Hipérbole é o lugar geométrico dos pontos de um plano cuja diferença das distâncias, em valor absoluto, a dois pontos fixos desse plano é constante. Consideremos no plano dois pontos distintos F_1 e F_2 tal que a distância d \left( F_1 , F_2 \right) = 2c . Seja um número real a tal que 2a < 2c . Ao conjunto de todos os pontos P do plano tais que: $$ \left| d \left(P , F_1 \right) – d \left( P , F_2 \right) \right| = 2a $$ ou $$ \left| |\vec{ P F_1 } | –  | \vec{P F_2}| \right| = 2a $$ dá se o nome de hipérbole e é representada pela curva abaixo:

Leia nosso artigo sobre hipérboles e sobre seções cônicas:

• A Hipérbole: Um estudo desta Curva como uma Seção Cônica
  
• Compreendendo as Seções Cônicas: Um Guia Introdutório

Seções Cônicas: Hipérboles – 9 Exercícios Resolvidos com Soluções Detalhadas

1) Nos problemas abaixo, para cada uma das hipérboles, determine:

• a medida dos semi-eixos;
• um esboço do gráfico;
• os vértices;
• os focos;
• a excentridade;
• as equações das assíntotas

a) 9x^2 -7y^2 = 63

SOLUÇÃO: Observe que $$ 9x^2 -7y^2 = 63 \Rightarrow \frac{9}{63}x^2 – \frac{7}{63}y^2 = \frac{63}{63} \Rightarrow \frac{x^2}{7} – \frac{y^2}{9} = 1 $$ que é a equação reduzida  da hipérbole com eixo real sobre dos x . Daí, $$ a^2 = 7 \Rightarrow a = \sqrt{7} \qquad b^2 = 9 \Rightarrow b = 3$$ e como o sinal negativo está com a variável y sabemos que a hipérbole  tem focos sobre o eixo x . Como a = \sqrt{7} , temos que $$ A_1 ( – \sqrt{7} , 0 ) \qquad \text{e} \qquad A_2 ( \sqrt{7} , 0 ).$$ Para determinar os focos, precisamos do valor de c : $$ c^2 = a^2 + b^2 \Rightarrow c^2 = 9+7 = 16 \Rightarrow c = 4 .$$ Logo, os focos são $$ F_1 (-4,0) \qquad \text{e} \qquad F_2 (4,0) ,$$ a excentricidade é $$e = \frac{c}{a} = \frac{4}{\sqrt{7}},$$ as equações das assíntotas são y = \pm \dfrac{3}{\sqrt{7}} x e um esboço do gráfico desta hipérbole é dado abaixo:

b) x^2 -4y^2 +16 = 0

SOLUÇÃO: Observe que $$ x^2 -4y^2 = -16 \Rightarrow \frac{1}{-16}x^2 – \frac{4}{-16}y^2 = 1 \Rightarrow – \frac{x^2}{4^2} + \frac{y^2}{2^2} = 1 $$ que é a equação reduzida  da hipérbole com eixo real sobre dos y . Daí, $$ a^2 = 4 \Rightarrow a = 2 \qquad b^2 = 16 \Rightarrow b = 4 $$ e como o sinal negativo está com a variável x sabemos que a hipérbole  tem focos sobre o eixo y . Como a = 2 , temos que $$ A_1 ( 0 , -2 ) \qquad \text{e} \qquad A_2 (  0 , 2 ).$$ Para determinar os focos, precisamos do valor de c : $$ c^2 = 2^2 + 4^2 \Rightarrow c^2 = 4+16 = 20 \Rightarrow c = 2 \sqrt{5} .$$ Logo, os focos são $$ F_1 (0 , -2 \sqrt{5}) \qquad \text{e} \qquad F_2 (0 , 2 \sqrt{5}) ,$$ a excentricidade é $$e = \frac{c}{a} = \frac{2 \sqrt{5}}{2} = \sqrt{5},$$ as equações das assíntotas são y = \pm \dfrac{1}{2}x e um esboço do gráfico desta hipérbole é dado abaixo:

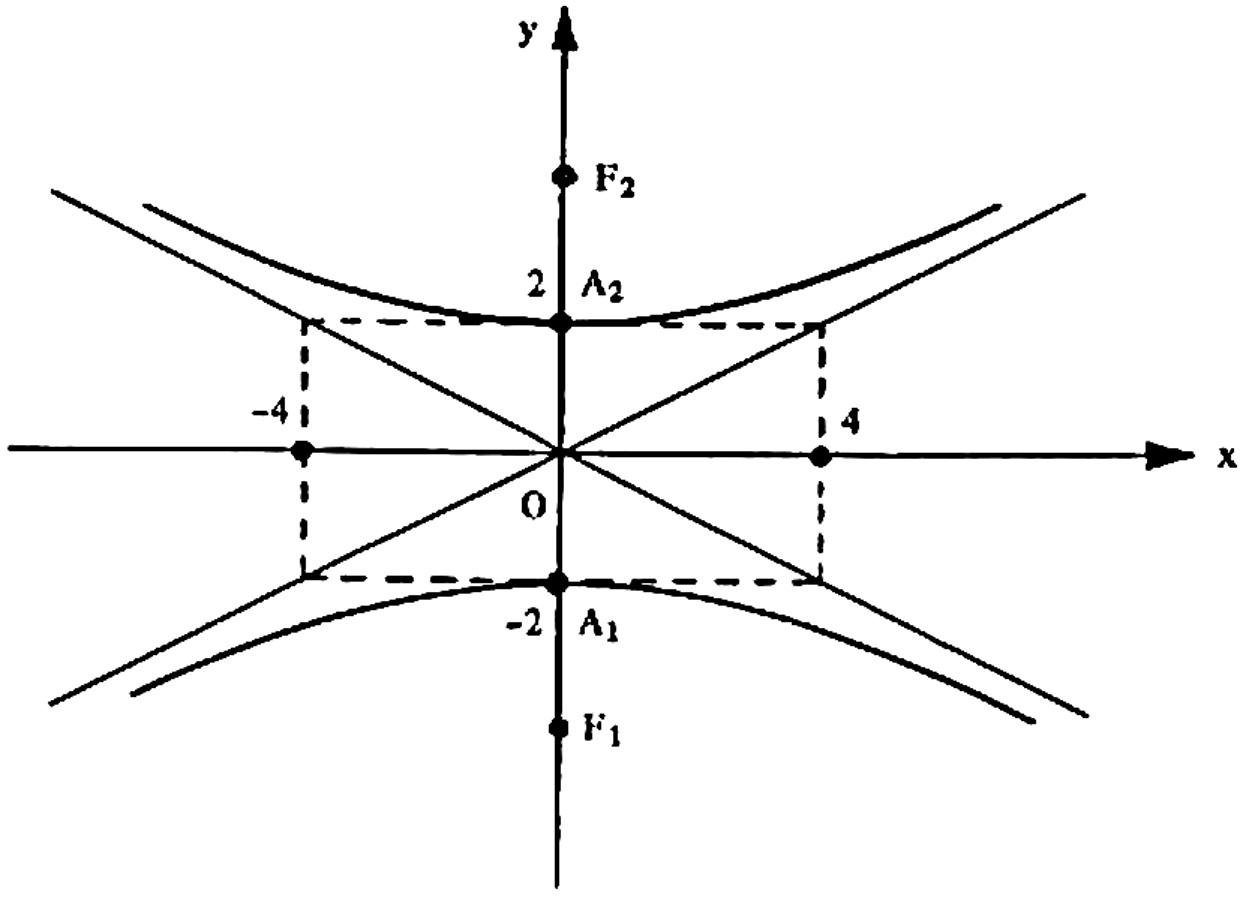
c) x^2 -y^2  = 4

SOLUÇÃO: Observe que $$ x^2 -y^2 = 4 \Rightarrow \frac{1}{4}x^2 – \frac{1}{4}y^2 = 1 \Rightarrow  \frac{x^2}{2^2} – \frac{y^2}{2^2} = 1 $$ Daí, $$ a^2 = 4 \Rightarrow a = 2 \qquad b^2 = 4 \Rightarrow b = 1 $$ e como o sinal negativo está com a variável y sabemos que a hipérbole  tem focos sobre o eixo x . Como a = 2 , temos que $$ A_1 ( -2,0 ) \qquad \text{e} \qquad A_2 ( 2,0 ).$$ Para determinar os focos, precisamos do valor de c : $$ c^2 = 2^2 + 2^2 \Rightarrow c^2 = 4+4 = 2 \sqrt{2}  .$$ Logo, os focos são $$ F_1 (-2 \sqrt{2} , 0) \qquad \text{e} \qquad F_2 (2 \sqrt{2} , 0) ,$$ a excentricidade é $$e = \frac{c}{a} = \frac{2 \sqrt{2}}{2} = \sqrt{2},$$ as equações das assíntotas são y = \pm x e um esboço do gráfico desta hipérbole é dado abaixo:

2) Uma hipérbole tem focos em F_1 (-5,0) e F_2 (5,0) e a medida do eixo real é igual a 6. Determine sua equação.

SOLUÇÃO: Tendo em vista que os focos são pontos do eixo dos x , a equação desta hipérbole é da forma $$ \frac{x^2}{a^2} – \frac{y^2}{b^2} = 1$$ Precisamos determinar  a e b . De F_1 (-5,0) e F_2 (5,0) , vem: $$c = 5$$ mas o eixo real mede $$2a = 6 \rightarrow a = 3 .$$ De $$c^2 = a^2 + b^2 \Rightarrow 25 = 9 + b^2 \Rightarrow b^2 = 16 $$ e, portanto, a equação procurada é $$ \frac{x^2}{9} – \frac{y^2}{16} = 1.$$

3) Determinar a equação da hipérbole de vértices A_1 (1,-2) e A_2 (5,-2) , sabendo que F_1 (6,-2) é um de seus focos.

SOLUÇÃO: Emm função dos dados do problema, vamos esboçar o gráfico desta hipérbole.

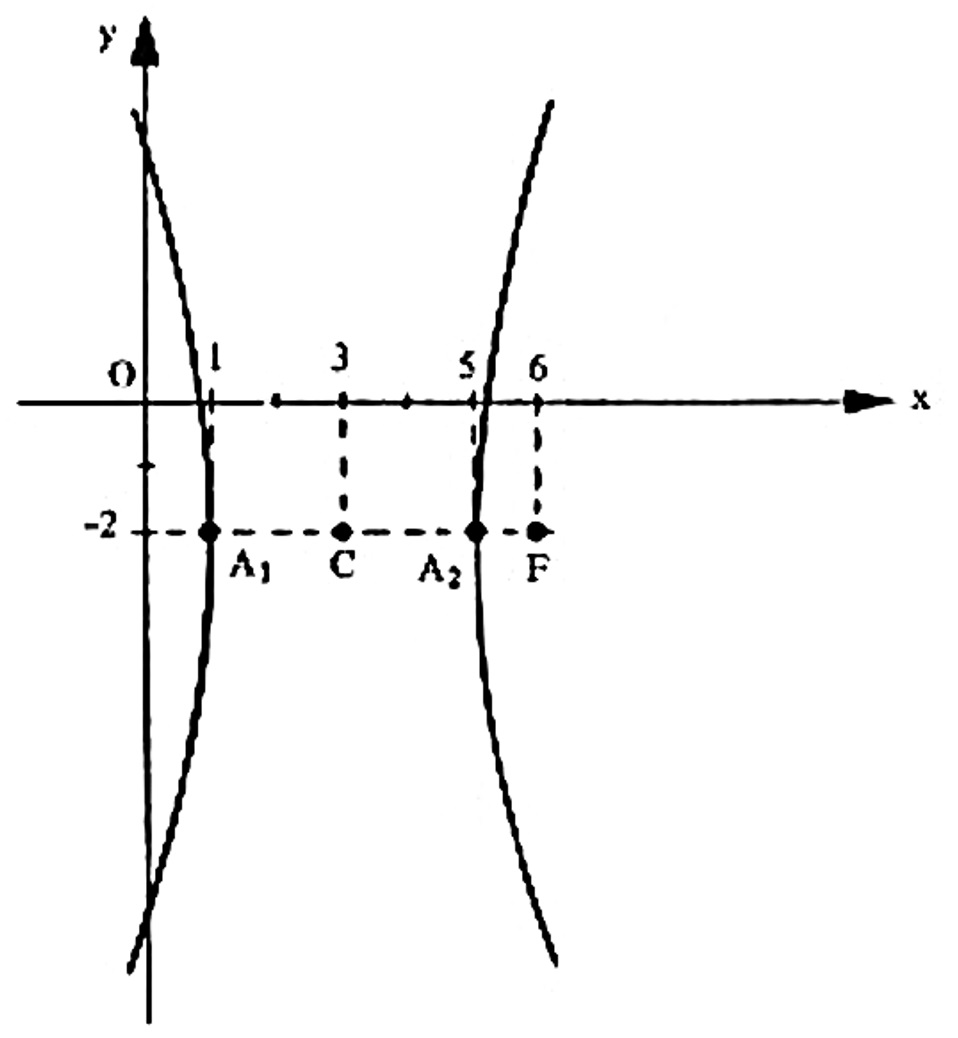
Sendo o eixo real paralelo ao eixo dos x , a equação da hipérbole é da forma $$ \frac{(x-h)^2}{a^2} – \frac{(y-k)^2}{b^2} = 1.$$ O centro é o ponto médio do segmento A_1 A_2 . Logo, C(3,-2) . É imediato que $$a = d(C , A_1 ) = 2 \qquad \text{e} \qquad c = d(C,F) = 3 .$$ Da relação $$c^2 = a^2 + b^2 $$ vem: $$ 9 = 4 + b^2 \Rightarrow b^2 = 5 .$$ Logo, a equação reduzida da hipérbole é dada por $$ \frac{(x-2)^2}{4} – \frac{(y+2)^2}{5} = 1.$$ Eliminando os denominadores e desenvolvendo os quadrados, encontramos $$ 5 \left( x^2-6x +9 \right) – 4  \left( y^2+4x +4 \right) = 20 $$ $$ 5 x^2 – 4 y^2-54 x+8y+113 = 0.$$

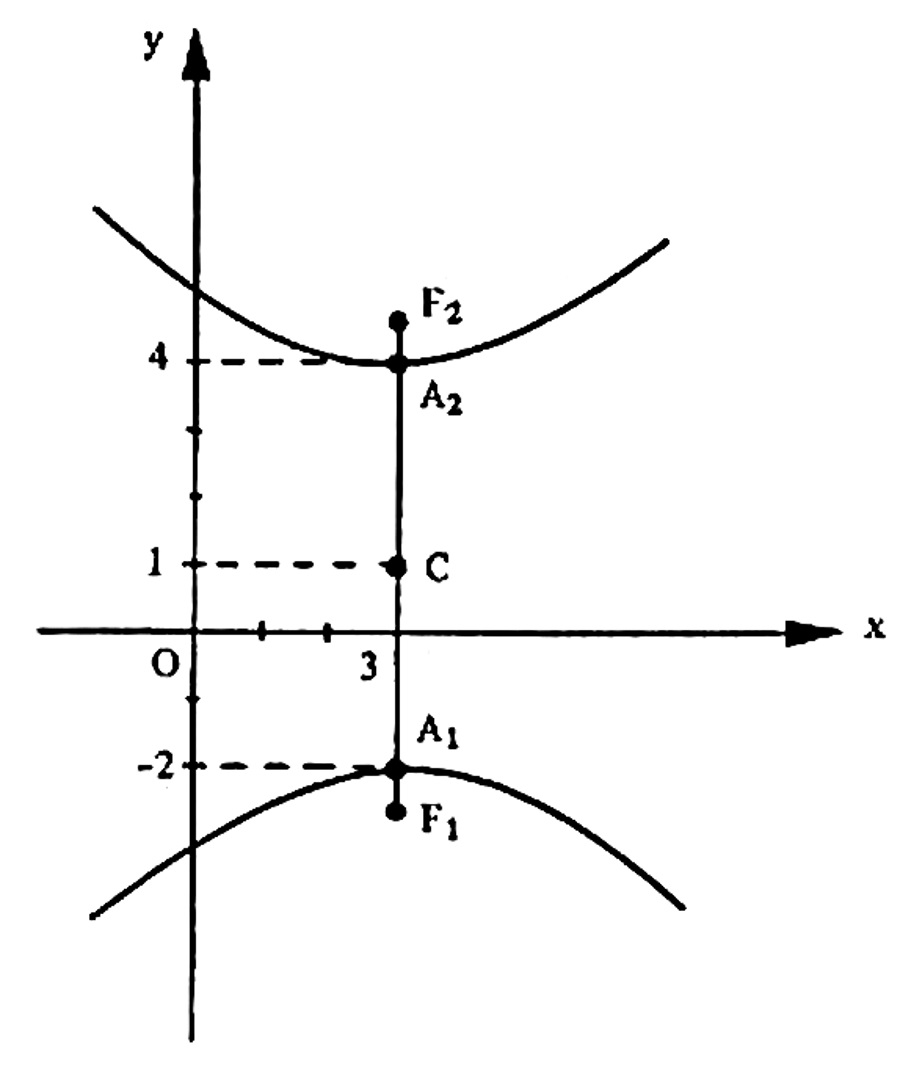
4) Determinar o centro, um esboço do gráfico, os vértices e os focos da hipérbole de equação $$9x^2-4y^2-54x+8y+113 = 0.$$

SOLUÇÃO: Primeiramente vamos conduzir  esta equação esta equação a uma das formas reduzidas. Agrupamos os termos de mesma variável, temos: $$9x^2-4y^2-54x+8y+113 = 0$$ $$ (9x^2-54x) – (4y^2 – 8y) = -113 $$ $$ 9( x^2 – 6x) – 4 (y^2 -2y) = -113 $$ $$ 9( x^2 – 6x +9) – 4 (y^2 -2y+1) = -113 +81 – 4 $$ $$ 9(x-3)^2 – 4(y-1)^2 = -36 $$ $$ – \frac{(x-3)^2}{4} + \frac{(y-1)^2}{9} = 1$$ que representa uma hipérbole de centro C(3,1) e eixo real paralelo ao eixo dos y . É imediato que: $$a^2 = 9 \qquad \text{e} \qquad b^2 = 4 $$ e, portanto: $$a =3 \qquad \text{e} b = 2. $$ pelo esboço do gráfico dado abaixo os demais elementos solicitados podem ser facilmente encontrados.

• Vértices: A_1(3,-2) e A_2 (3, 4) ;
• Focos: para determinar os focos precisamos conhecer o valor de c . $$ c^2 = a^2 +b^2 \Rightarrow c^2 = 9 + 4 = 13 \Rightarrow c = \sqrt{13}.$$ Logo, os focos são  F_1 (3,1 - \sqrt{13}) e F_2 (3, (3,1 + \sqrt{13})  ;

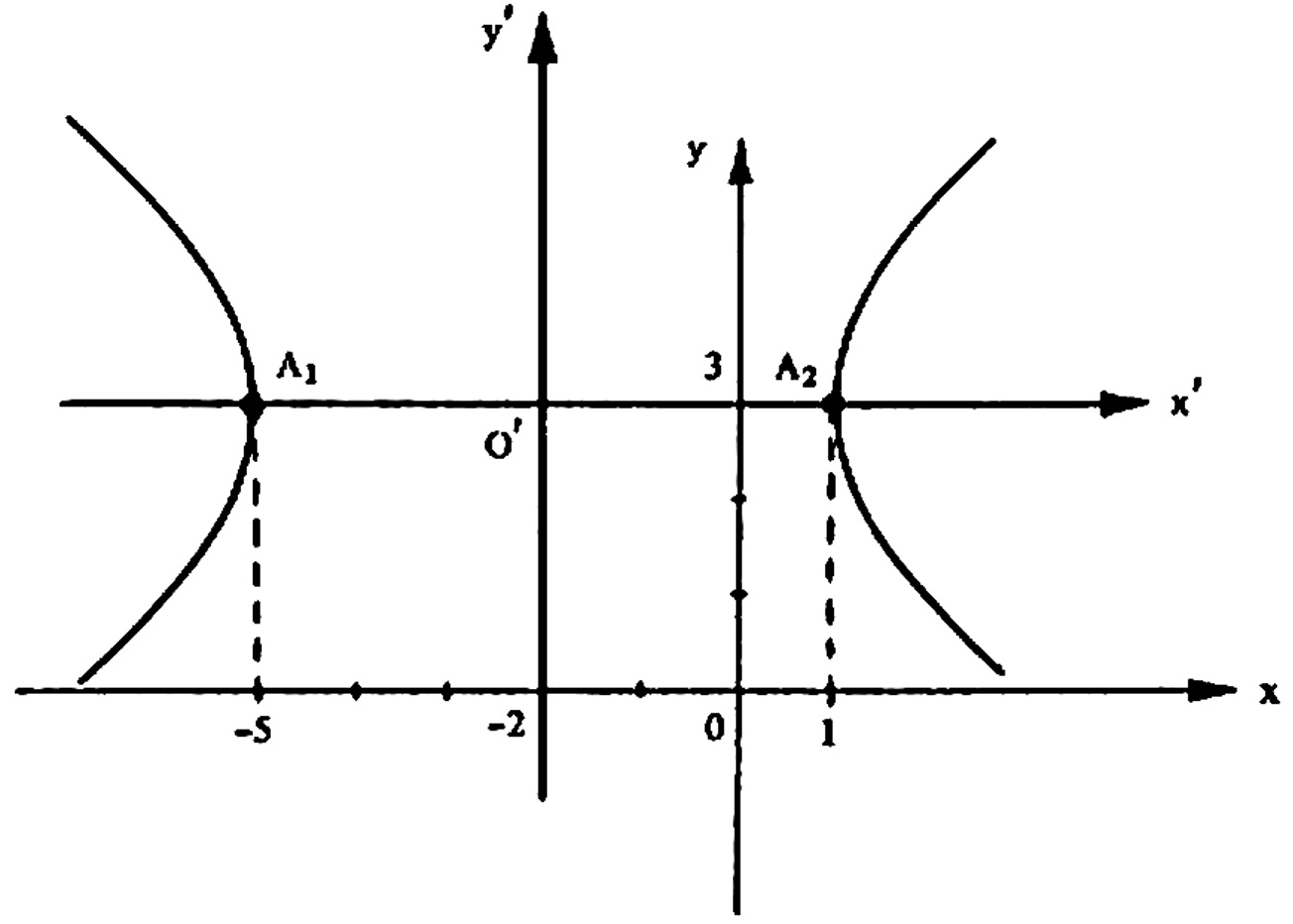
5) Obter a equação reduzida resultante de uma translação de eixos, classificar, dar os elementos e oesboçar o gráfico da equação $$7x^2-9y^2+28x+54y-116 = 0.$$

SOLUÇÃO: Do mesmo que no problema anterior, mudemos a equação dada para a forma: $$ \frac{(x-h)^2}{a^2} – \frac{(y-k)^2}{b^2} = 1.$$ Assim $$7x^2-9y^2+28x+54y-116 = 0$$  $$ (7x^2 + 28 x) – (9y^2 – 54 y) = 116 $$ $$ 7 (x^2 + 4 x) – 9 (y^2 – 6 y) = 116 $$ $$ 7 (x^2 + 4 x +4) – 9 (y^2 – 6 y +9) = 116 +28 -81 $$  $$ 7 (x+2)^2 – 9 (y-3) ^2 = 63 $$ $$ \frac{7 (x+2)^2}{63} – \frac{9 (y-3) ^2}{63} = 1 $$ $$ \frac{(x+2)^2}{9} – \frac{ (y-3) ^2}{7} = 1 $$  Logo, $$ a^2 = 9 \qquad \text{e} \qquad b^2 = 7 $$ $$ \text{eixo real:} 2a = 6 \qquad \text{e} \qquad \text{eixo imaginário: } 2b = 2 \sqrt{7}$$ e $$a = 3 \qquad \text{e} \qquad b = \sqrt{7}$$ $$c^2 = a^2 + b^2 \Rightarrow c^2 = 9+7 \Rightarrow c = 4$$ e os focos são dados por F_1 (-6,3) e F_2 (2,3) . Esboço do gráfico:

6) Ache as equações da hipérbole e das suas assíntotas, conhecendo:

a) os focos F_1 (-\sqrt{13},0) e F_2 (\sqrt{13},0) e a medida do eixo transverso, 6;

SOLUÇÃO: Temos 2a = 6 e 2c = 2 \sqrt{13} , logo a = 3 e c = \sqrt{13} . Daí, b^2 = c^2 - a^2 = 4 . Como os focos estão no eixo Ox , daí, $$\frac{x^2}{9} – \frac{y^2}{4} = 1 $$ e as assíntotas têm equações $$ y= \pm \frac{2}{3}x .$$

b) um foco F_1 (0, -\sqrt{11}) , a distância focal 2 \sqrt{11} , e a medida do eixo conjugado 2 \sqrt{7} , sabendo que o outro foco está sobre o eixo Oy.

SOLUÇÃO: Temos 2b = 2 \sqrt{7} , 2c = 2 \sqrt{11} , portanto b =  \sqrt{7} , c =  \sqrt{11} . Daí, a^2 = c^2 - b^2 = 4 . Como os focos estão em Oy , temos que $$ – \frac{x^2}{7} + \frac{y^2}{4} = 1$$ As assíntotas têm equações dadas por $$ y = \pm \frac{2}{\sqrt{7}}x.$$

Leia Mais Sobre Seções Cônicas

• Seções Cônicas: Parábola | 10 Exercícios Resolvidos
• Seções Cônicas: Elipse | 8 Exercícios Resolvidos com Soluções Detalhadas
• Compreendendo as Seções Cônicas: Um Guia Introdutório
• A Parábola: Um estudo desta curva como seção cônica
• A Elipse: Um estudo desta Curva como uma Seção Cônica
• A Hipérbole: Um estudo desta Curva como uma Seção Cônica