Seções Cônicas: Parábola | 10 Exercícios Resolvidos

Melhore sua compreensão de parábolas como curvas planas geradas por seções cônicas com estes 10 exercícios resolvidos com soluções detalhadas. Perfeito para estudantes de graduação em ciências exatas e da terra.

Se você está procurando melhorar sua compreensão das parábolas como curvas planas geradas por seções cônicas, você veio ao lugar certo. Neste artigo, forneceremos 10 exercícios resolvidos com soluções detalhadas para ajudá-lo a dominar esse importante conceito matemático. Seja você um estudante de graduação em ciências exatas e da terra, esses exercícios irão ajudá-lo a aprimorar suas habilidades e aprofundar sua compreensão das parábolas como seções cônicas.

O que é uma parábola como curva plana gerada por seção cônica?

Uma parábola é um tipo de seção cônica definida como o conjunto de todos os pontos em um plano que são equidistantes de um ponto fixo (chamado de foco) e uma linha fixa (chamada de diretriz). Uma parábola é gerada se \pi cortar um cone paralelo à geratriz r;

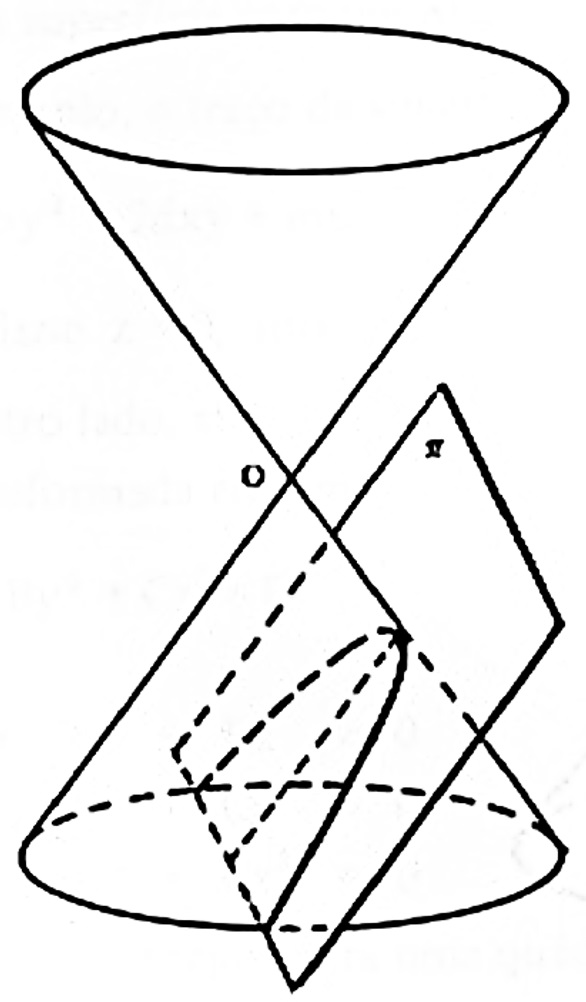
A forma de uma parábola é semelhante à de uma curva em forma de U, com o vértice sendo o ponto mais baixo ou mais alto da curva, dependendo de sua orientação. O foco e a diretriz de uma parábola estão localizados no eixo de simetria, que é uma linha que divide a parábola em duas metades iguais.

Leia nosso artigo sobre párabolas e sobre seções cônicas:

• A Parábola: Um estudo desta curva como seção cônica
• Compreendendo as Seções Cônicas: Um Guia Introdutório

Seções Cônicas: Parábola – 10 Exercícios Resolvidos com Soluções Detalhadas

1) Determine o foco e a equação da diretirz das parábolas abaixo e construa seus gráficos:

a)   x^2 = 8 y

Solução: Esta é uma equação de uma parábola com o eixo sobre o eixo Oy e vértice na origem do sistema. Logo, por este artigo sabemos que sua equação tem a forma: $$ x^2 = 2p y.$$  Daí, podemos ver que $$ 2p = 8 \Rightarrow p = 4 \Rightarrow \frac{p}{2} = 2.$$ Portanto, sabemos que a distância entre o vértice e o foco é igual a 2, que é mesma distância entre o vértice e a reta diretriz. Além disso, como p > 0 sabemos que esta parábola possui concavidade para cima. Logo, podemos concluir que $$ \text{Foco: } F(0,2) \qquad \text{diretriz: } y = -2 .$$

b)   y^2 = -2x

Solução: Já esta é a equação de uma parábola com o eixo sobre o eixo Ox e vértice na origem do sistema. Logo, por este artigo sabemos que sua equação tem a forma: $$ y^2 = 2p x.$$  Daí, podemos ver que $$ 2p = -2 \Rightarrow p = -1 \Rightarrow \frac{p}{2} = – \frac{1}{2}.$$ Portanto, sabemos que a distância entre o vértice e o foco é igual a - \dfrac{1}{2} , que é mesma distância entre o vértice e a reta diretriz. Além disso, como p < 0 sabemos que esta parábola possui concavidade para a esquerda. Logo, podemos concluir que $$ \text{Foco: } F \left(- \frac{1}{2}, 0 \right) \qquad \text{diretriz: } x = \frac{1}{2} .$$

2) Determinar a equação de cada uma das parábolas abaixo, sabendo que todas possuem o vértice no ponto V(0,0) e que:

a) Foco: F(1,0)

Solução: Como o foco está sobre o eixo Ox, sabemos que o eixo da parábola também está sobre este eixo, logo, por este artigo sabemos que sua equação tem a forma: $$ y^2 = 2p x.$$ Como a distância do foco F(1,0) ao vértice V(0,0) é igual a \dfrac{p}{2} , sabemos que $$ p = 2 .$$ Substituindo este valor na equação da parábola, obtemos $$ y^2 = 4x.$$

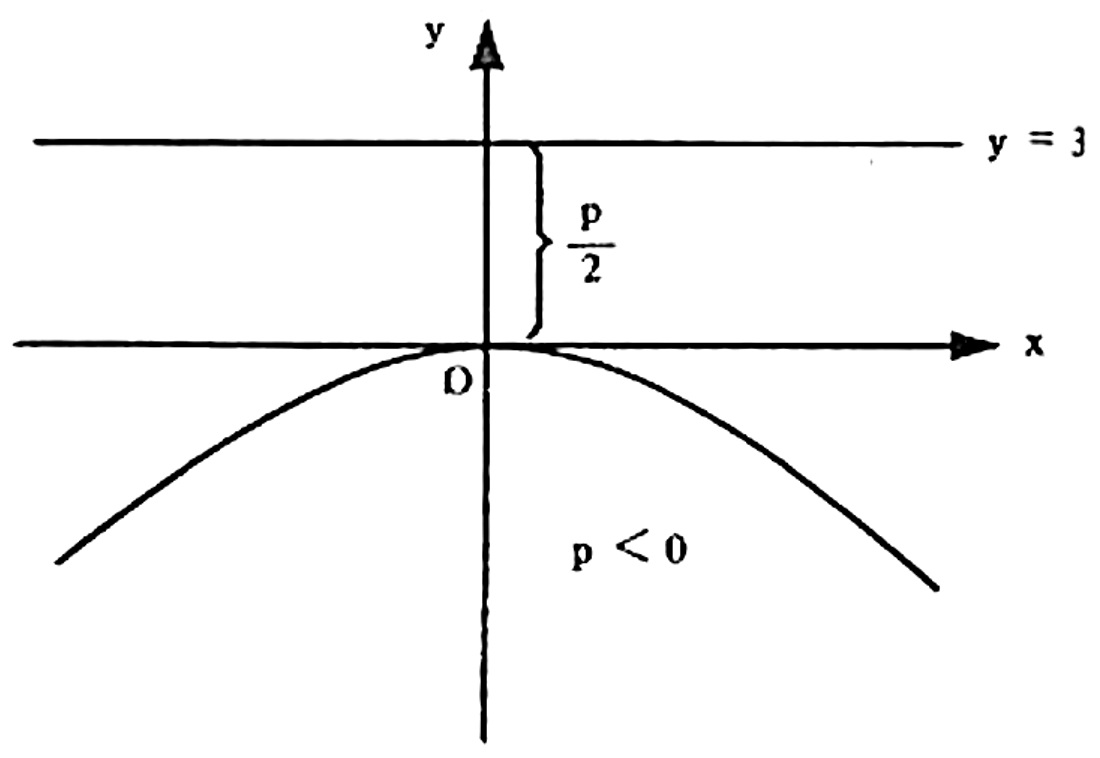
b) Diretriz y =3

Solução: Sendo a diretriz dada pela equação y = 3 , então sabemos que esta é uma reta paralela ao eixo Ox. Logo, como o vértice está sobre a origem do plano cartesiano, então o foco está sobre o eixo Oy, no ponto F(0,-3) , o que nos diz que a cocavidade está virad a para baixo. Desta forma,  por este artigo sabemos que sua equação tem a forma: $$ x^2 = 2p y $$ e que \dfrac{p}{2} =  - 3 , pois a concavidade da parábola será para baixo. Portanto, p = -6 e podemos garantir que a equação desta parábola será $$ x^2 = -12 y .$$

c) passa pelo ponto P(-2,5) e tem concavidade voltada para cima.

Solução: Como a parábola tem concavidade para cima e seu vértice está na origem do sistema, podemos afirmar que p>0 e que seu foco está sobre o eixo Oy. Logo sua equação será dada por $$ x^2 = 2p y .$$ Sendo P um ponto desta parábola, suas coordenadas satizfazem sua equação. Logo $$(-2)^2 = 2 p (5) \Rightarrow 4 = 10 p \Rightarrow p = \frac{2}{5}.$$ Portanto, a equação desejada é dada por $$ x^2 = \frac{4}{5} y \Rightarrow 5x^2 – 4y = 0.$$

3) Determinar a equação da parábola de vértice V(3,-1) , sabendo que y - 1 = 0 é a equação de sua diretriz

Solução: Para facilitar, façamos um esboço do gráfico.

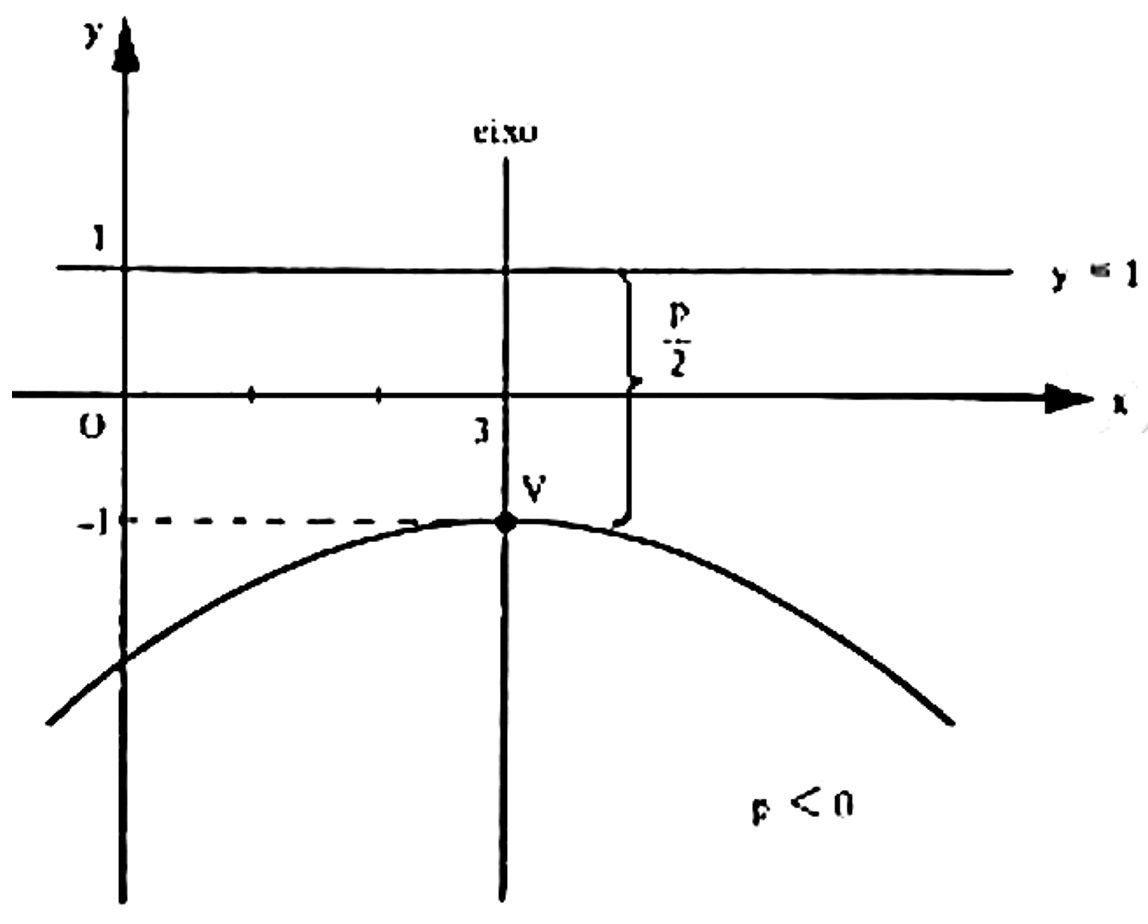
A equação da parábola é da forma $$ (x-h)^2 = 2p (y-k)$$ e usando o esboço acima temos que $$ h = 3, \qquad k = -1, \qquad \frac{p}{2} = -1 \Rightarrow p = -4.$$ Substituindo na equação da parábola temos $$ (x-3)^2 = 2(-4) (y+1)$$ $$ x^2 -6x +9 = -8y -8 $$ $$x^2 – 6x + 8y +17 = 0.$$

4) Determinar a equação da parábola de foco em F(1,2) , sendo x = 5 a equação da diretriz.

Solução: Como a equação da diretriz, x = 5 , nos diz que ela é paralela ao eixo Oy, então o eixo da parábola é parálelo ao eixo Ox  e a equação da parábola é da forma  $$(y-k)^2 = 2p (x – h).$$ Como a coordenada x do foco esta à esquerda da reta diretiz, podemos garantir que a concavidade da parábola é para a esquerda e $$ p = 1-5 = -4.$$  Além disso, o vértice V(3,2) é o ponto médio do segmento AF, sendo A(5,2) , um ponto de interseção entre o eixo e a reta diretriz. Substituindo na equação, obtemos $$ (y-2)^2 = 2 (-4)(x-3) $$ $$ y^2 -4y +4 = -8x +24 $$ $$y^2 – 4y +8x -20 = 0.$$

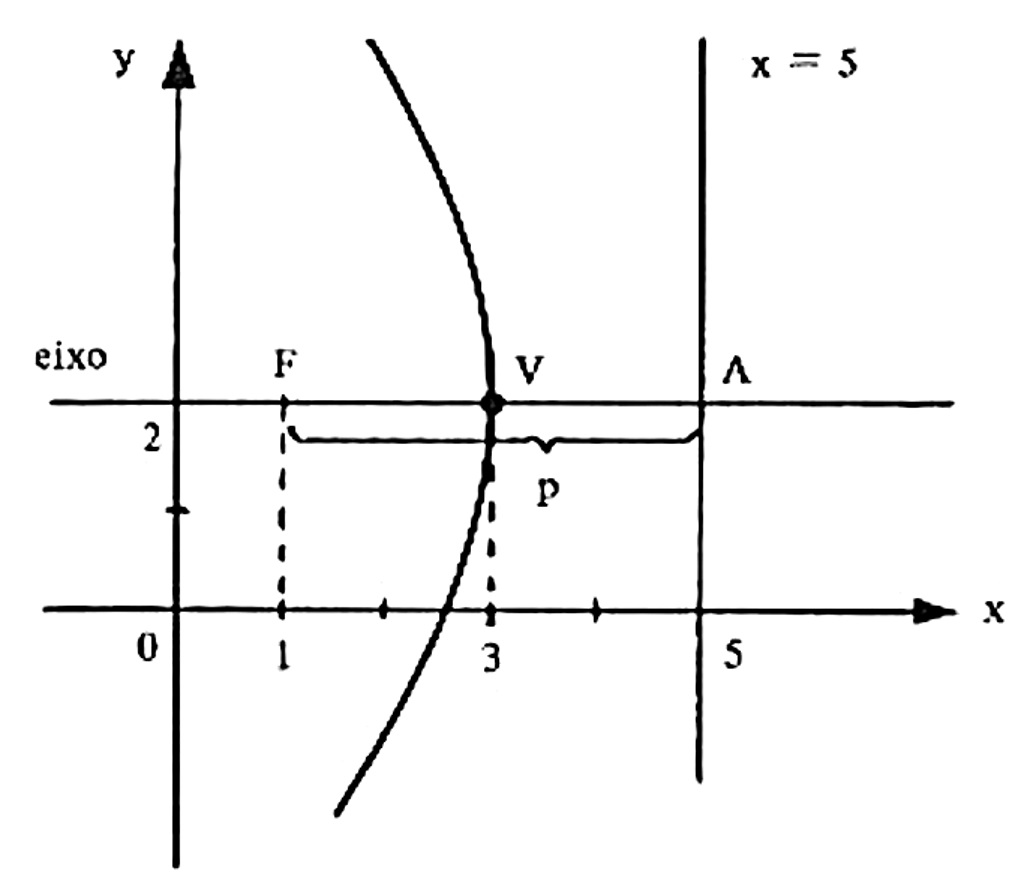
5) Determinar o vértice, um esboço do gráfico, o foco e a equação da diretriz da parábola $$y^2 + 6 y – 8x +1 = 0 .$$

Solução: Neste caso, precisamos efetuar uma manipulação algébrica simples para colocar a equação na forma (y-k)^2 = 2p (x - h) : $$ y^2 + 6 y – 8x +1 = 0 \\ y^2 +6y +9 -8x – 8 = 0 \\ y^2 +6y +9 = 8x +  8 \\ (y+3)^2 = 8(x+1) \\ (y+3)^2 = 2 (4) (x+1) .$$ Dái, podemos concluir que $$ p = 4 \Rightarrow \frac{p}{2} = 2 \Rightarrow \text{concavidade para a direita} \\ \text{ Vértice: } V(-1,-3) .$$ Pelo esboço do gráfico abaixo, podemos concluir que os elementos solicitados são $$ \text{Foco: } F(1,-3) \\ \text{diretriz: } x = -3.$$

6) Determinar a equação da parábola que passa pelos pontos (0,1) , (1,0) e (3,0) , conforme a figura

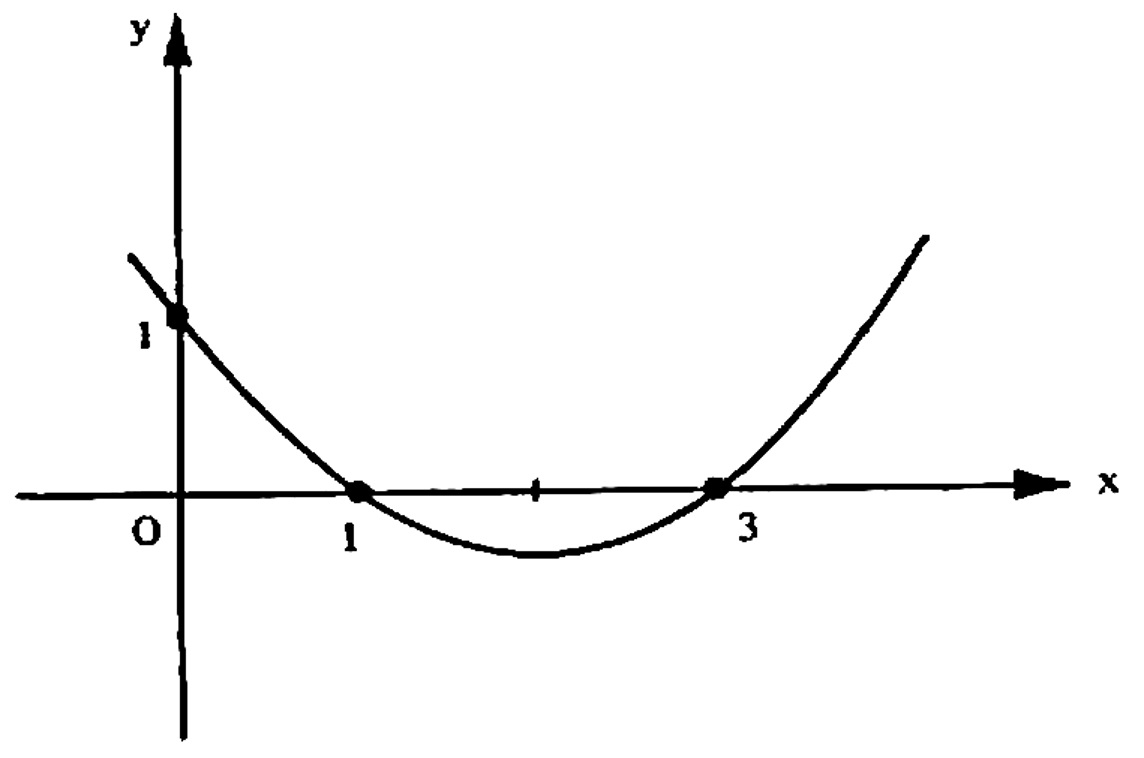
Solução: A  equação explícita desta parábola é da forma $$y = ax^2 +bx +c.$$ Logo, estes três pontos precisam satisfazer a equação da parábola. Ou seja, os coeficientes a , b e c precisam satisfazer simultaneamente as equações $$ 1 = a(0)^2 + b(0)+c $$ $$0 = a(1)^2 +b(1) + c $$ $$0 = a(3)^2 + b(3) + c $$ ou seja, $$c=1$$ $$a+b+c=0$$ $$9a + 3b +c = 0$$ um sistema linear cuja solução é $$ a = -\frac{1}{3}, \qquad b = – \frac{4}{3}, \qquad c= 1.$$ Logo, a equação da parábola é $$ y = \frac{1}{3} x^2 – \frac{4}{3}x +1 .$$

7) Encontre a equação reduzida da parábola que tem equação explícita dada por x^2-6x-4y+17 = 0.

Solução: Manipulando algebricamente a equação explícita temos:  $$ x^2 – 6x +9 -4y +17 -9 = 0 $$ $$ (x-3)^2 – 4 (y-2) = 0 $$ $$ (x-3)^2 = 4(y-2) $$ $$ (x-3)^2 = 2 (2) (y-2) .$$ Portanto, a equação reduzida da parábola é $$ (x-3)^2 = 2 (2) (y-2).$$

Leia Mais Sobre Seções Cônicas

• Compreendendo as Seções Cônicas: Um Guia Introdutório
• A Parábola: Um estudo desta curva como seção cônica
• A Elipse: Um estudo desta Curva como uma Seção Cônica
• A Hipérbole: Um estudo desta Curva como uma Seção Cônica