Introdução às Superfícies: Parametrização, Suavidade e Cálculo de Área.

Nesse artigo queremos estudar superfícies com o intuito de usar esse estudo para resolver as integrais de superfícies.

Para isso, precisamos saber como representar analiticamente essas superfícies.

Uma superfície \mathbb{S} no \mathbb{R} ^3 pode ser representada implicitamente na forma f(x,y,z) = 0.

Esse tipo de função f(x,y,z) é chamada de Campo Escalar, ou Função de Várias Variáveis a Valores Reais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar.

De modo explícito, a mesma superfície \mathbb{S} pode ser dada por uma função vetorial dada por z=g(x,y), ou seja, uma função de duas variáveis reais a valores reais.

Vamos entender como.

REPRESENTAÇÃO EXPLÍCITA E IMPLÍCITA DE SUPERFÍCIES

Uma superfície \mathbb{S} no \mathbb{R} ^3 pode ser representada implicitamente na forma f(x,y,z) = 0, onde \nabla f(x,y,z) é o vetor normal à superfície e, se \nabla f \neq 0, então o vetor $$\vec{n} = \frac{\nabla f}{\left\| \nabla f \right\|}$$ é o vetor normal unitário de \mathbb{S}.

De modo explícito, a mesma superfície \mathbb{S} pode ser dada por uma função vetorial dada por z=g(x,y).

Para encontrarmos esta forma explícita basta isolar a variável z na forma implícita da superfície \mathbb{S}.

REPRESENTAÇÃO PARAMÉTRICA DE UMA SUPERFÍCIE

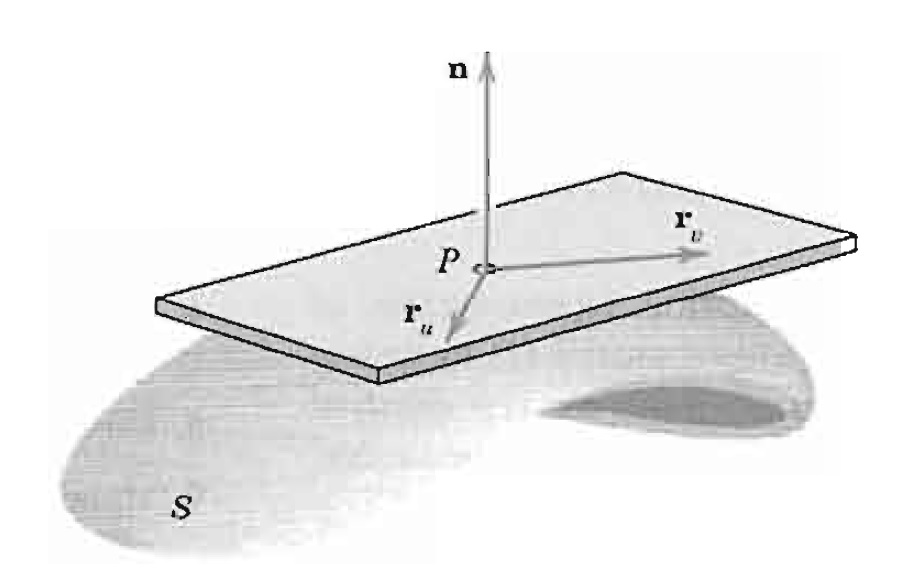
Uma superfície \mathbb{S} pode ser representada de modo paramétrico na forma $$r(u,v) = x(u,v)\vec{i} + y(u,v)\vec{j} + z(u,v)\vec{k}.$$

Como ilustrado na figura abaixo, essa parametrização leva cada ponto (u,v) da região R no ponto da superfície com vetor posição dado por \vec{r}(u,v) .

PLANO TANGENTE E SUPERFÍCIE NORMAL

No artigo dedicado ao plano tangente ao gráfico de uma função z=f(x,y) , que você confere aqui, estabelecemos que esse plano só existe nos pontos onde a função é diferenciável.

Portanto, o vetor normal a esse plano, que seria o vetor diretor na reta normal ao gráfico dessa mesma função, será também o vetor normal à superfície em cada ponto.

Tanto que nos parágrafos anteriores definimos esse vetor normal no caso onde a superfície é representada analiticamente de forma explícita ou implícita.

Agora, se a superfície \mathbb{S} está escrita em sua forma paramétrica $$r(u,v) = x(u,v)\vec{i} + y(u,v)\vec{j} + z(u,v)\vec{k},$$ então $$\vec{n} = \frac{\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v}}{\left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\|}$$ é o vetor normal unitário da superfície.

O QUE SÃO SUPERFÍCIES SUAVES?

DEFINIÇÃO (SUPERFÍCIE SUAVE): Uma superfície \mathbb{S} é chamada de superfície suave se sua superfície normal depende continuamente dos pontos de \mathbb{S}, ou seja, em cada ponto de uma superfície suave existe um único plano tangente à ela ligada a esse ponto.

Outra forma de garantir se uma superfície é suave é se em cada parte dessa superfície existir uma parametrização \vec{r}(u,v) = x(u,v)\vec{i} + y(u,v)\vec{j} + z(u,v)\vec{k} , tal que as funções x(u,v), z(u,v), e z(u,v) admitam derivadas parciais contínuas de todas as ordens e que, para todo (u_0, v_0) sobre a região contida no domínio da parametrização que gera a superfície, os vetores  $$\frac{\partial \vec{r}}{\partial u}(u_0, v_0) \;\;\; e \;\;\; \frac{\partial \vec{r}}{\partial v}(u_0, v_0)$$ sejam linearmente independentes.

Essa condição, é conhecida como condição de suavidade ou regularidade da superfície.

Os pontos da superfície onde a condição de suavidade não pode ser garantida são chamados de pontos singulares. 

Uma má escolha da parametrização pode nos levar a pontos onde a condição de suavidade não é verificada, mesmo que a superfície seja suave. Estes pontos são chamados de pontos singulares falsos.

DEFINIÇÃO (SUPERFÍCIE SUAVE POR PARTES): Uma superfície \mathbb{S} é chamada de superfície suave por partes se é constituída de uma quantidade finita de porções de superfícies suaves.

O QUE SÃO SUPERFÍCIES ORIENTÁVEIS?

Dada uma superfície suave, em cada ponto temos dois vetores normais unitários com mesma direção, mas sentidos opostos. Se for possível escolher um desses vetores de maneira contínua em toda a superfície, então dizemos que a superfície é orientável.

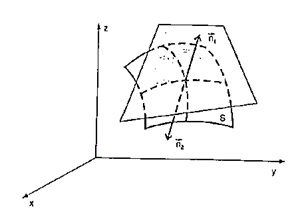
Desta forma, se a parametrização da superfície é dada por $$\vec{r}(u,v) = x(u,v)\vec{i} + y(u,v)\vec{j} + z(u,v)\vec{k},$$ então, nos pontos onde as condições de suavidade são satisfeitas, os vetores $$\vec{n_1} = \frac{\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v}}{\left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\|}\;\;\; e \;\;\;\ \vec{n_2} = – \vec{n_1}$$ são os vetores unitários normais à superfície.

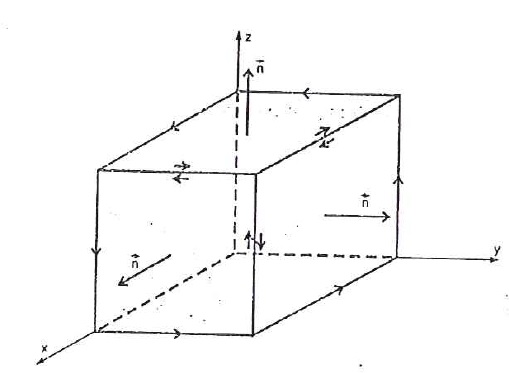
Se uma superfície e suave por partes, podemos orientá-la se cada uma de suas partes é limitada por uma curva simples fechada. A figura abaixo mostra uma possível orientação da superfície de um cubo, denominada superfície exterior do cubo:

EXEMPLO (PARAMETRIZAÇÃO DO PLANO):

O plano \pi que tem vetor normal \vec{n} = (a,b,c) e passa pelo ponto A(x_0 , y_0, z_0 ) é dado implicitamente por $$ax+by+cz+d = 0$$ onde d = -ax_0 -by_0 -cz_0 .

As equações paramétricas do plano \pi são dadas por

$$ \pi: \vec{r} (u,v) = \left(  x_0 + u a_1 + v a_2 , y_0 + u b_1 + v b_2 , z_0 + u c_1 + v c_2 \right) = $$ $$ =(x_0 , y_0 , z_0 ) + u (a_1 , b_1 , c_1 ) + v (a_2 , b_2 , c_2 ) = A + u \vec{w_1} + v  \vec{w_2}.$$

onde u,v \in \mathbb{R} , \vec{w_1} = (a_1 , b_1 , c_1 )  e \vec{w_2} = (a_2 , b_2 , c_2 )  e $$ \vec{w_1} \wedge \vec{w_2} = \lambda \vec{n} .$$

Essa é uma superfície suave.

EXEMPLO (PARAMETRIZAÇÃO DA ESFERA):

Uma esfera com centro na origem e raio a pode ser representada pela função $$f(x,y,z,) = x^2+y^2+z^2-a^2=0.$$

Por essa representação podemos escrever o vetor normal unitário à esfera como sendo $$\vec{n} (x,y,z) = \left( \frac{x}{a}, \frac{y}{a}, \frac{z}{a} \right)$$.

Ou seja, os vetores normais possuem a direção dos vetores posição (x,y,z) de cada ponto correspondente.

Dessa representação implícita podemos encontrar as funções $$z = g_1 (x,y) = \sqrt{a^2 – x^2 – y^2}$$ $$z =  g_2 (x,y) = – \sqrt{a^2 – x^2 – y^2}$$ que são representações explícitas das superfícies superior e inferior ao plano xy da esfera, respectivamente.

Já a parametrização da esfera é dada por:

$$r(u,v) = (a\cos{u}\cos{v})\vec{i} + (a\sin{u}\cos{v})\vec{j} + (a\sin{v})\vec{k},$$
onde 0\leq u \leq 2\pi e 0 \leq v \leq \pi.

Essa é uma superfície suave.

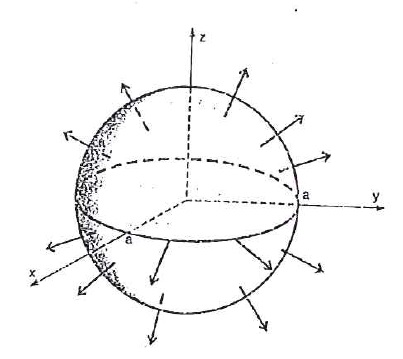
Além de suave, podemos observar que o campo vetorial normal à essa esfera é definido por $$\vec{n_1} = (cos(v) cos(u), cos(v) sen(u), sen(v)); \;\;\;se\;\; v \neq \pm \pi/2$$ $$\vec{n_1} = (0,0,1); \;\;\;se\;\; v = \pi/2$$ $$\vec{n_1} = (0,0,-1); \;\;\;se\;\; v = – \pi/2.$$

Todos esse vetores podem ser ilustrados na figura abaixo:

EXEMPLO (PARAMETRIZAÇÃO DO CILINDRO):

O cilindro circular $$x^2+y^2 = a^2; \;\; -1 \leq z \leq 1$$ tem raio igual a a, altura igual a 2 e o eixo z o eixo do cilindro.

Uma representação paramétrica do cilindro é dada por:

$$r(u,v) = (a\cos{u})\vec{i} + (a\sin{u})\vec{j} + (v\vec{k}),$$
onde 0\leq u \leq 2\pi e v \in [-1,1].

Essa é uma superfície suave.

EXEMPLO (PARAMETRIZAÇÃO DO CONE):

Um cone circular $$z = \sqrt{x^2 + y^2}, \;\;\; 0 \leq z \leq H,$$ pode ser representada por $$ \vec{r} (u,v) = u cos(v) \vec{i} + u sen(v) \vec{j} + u \vec{k},$$ onde 0\leq u \leq H e 0\leq v \leq 2 \pi .

No caso do cone, o vetor normal unitário \vec{n} fica indeterminado pois, usando a forma implícita de sua representação $$g(x,y,z) = -z + \sqrt{x^2 + y^2} = 0$$, encontramos  $$\vec{n} (x,y,z) = \left( \frac{x}{\sqrt{2(x^2+y^2)}},  \frac{y}{\sqrt{2(x^2+y^2)}} , -\frac{1}{\sqrt{2}}\right).$$

Essa não é uma superfície suave.

EXEMPLO (A FAIXA DE MOBIUS):

Uma fita de Mobios ou faixa de Mobios é um espaço topológico obtido pela colagem das duas extremidades de uma fita, após efetuar meia volta em uma delas.

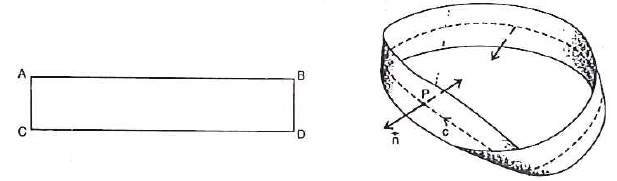
Deve o seu nome a August Ferdinand Möbius, que a estudou em 1858 tendo em vista a obtenção de um prêmio da Academia de Paris sobre a teoria geométrica dos poliedros.

A parametrização desta curiosa superfície é dada por $$ \vec{r} (u,v) = \left( 1 + v sen \left(\frac{u}{2}\right) \right) cos(u) \vec{i} + \left( 1 + v sen \left(\frac{u}{2}\right) \right) sen(u) \vec{j} + \left( 1 + v cos \left( \frac{u}{2}\right) \right) \vec{k},$$ onde -1 \leq v \leq 1 e 0 \leq u \leq 2 \pi .

Podemos observar que escolhido um vetor normal unitário em algum ponto desta superfície, quando esse vetor se desloca continuamente sobre a superfície e retorna a seu ponto original, o sentido do vetor se inverte.

Por isso, a Faixa de Mobius é uma superfície não-orientável, apesar de ser suave. Acredite que isso é mais fácil de observar do que demonstrar matematicamente.

Motivados por isso, listamos abaixo algumas observações sobre a faixa de Möbius:

1. É uma superfície com uma componente de fronteira;
2. Não é orientável.
3. Possui apenas um lado.
4. Possui apenas uma borda.
5. Representa um caminho sem fim nem início, infinito, onde se pode percorrer toda a superfície da fita que aparenta ter dois lados, mas só tem um.

Área da Superfície

A área A de uma superfície \mathbb{S} é definida pela integral dupla $$A = \int \int_{R}{dA},$$ onde

1. dA = \left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\| dudv, se \mathbb{S} é denotada em sua forma paramétrica r(u,v);
2.  dA = \sqrt{1+\left( \frac{\partial g}{\partial x}\right)^2 + \left( \frac{\partial g}{\partial y}\right)^2}dxdy se \mathbb{S} é denotada em sua forma explícita z=g(x,y)

EXEMPLO

Calcule a área da superfície esférica com centro na origem e raio a>0.

Sabemos que $$A = \int \int_{R}{dA},$$ onde R é o círculo com centro na origem e raio igual a a.

Observe que a superfície da esfera acima do plano xOy pode ser escrita como $$g(x,y) = \sqrt{a^2 -x^2 – y^2},$$  e a área total da esfera é o dobro do valor dessa área.

Logo, $$A = \int \int_{R}{dA} = 2 \int \int_{R}{\sqrt{1+\left( \frac{\partial g}{\partial x}\right)^2 + \left( \frac{\partial g}{\partial y}\right)^2}dxdy}$$ onde R é o círculo com centro na origem e raio a.

Ou seja, $$A = \int \int_{R}{\sqrt{1+ \frac{x^2 + y^2}{a^2 – x^2 – y^2}}dxdy} = \int_{0}^{2 \pi} \int_{0}^{a}{\sqrt{\frac{a^2}{a^2 – r^2}}r dr d \theta}=$$ $$= 2 \pi \int_{0}^{a}{\sqrt{\frac{a^2}{a^2 – r^2}}}r dr = 4 \pi a^2$$

EXEMPLO

Calcule a área da superfície do parabolóide  z= 2(x^2+y^2), abaixo do plano z=8 .

A parametrização desse parabolóide é dada por $$\vec{r}(u,v) = u\vec{i} + v\vec{j} + 2(u^2+v^2)\vec{k},$$ definida sobre a região $$ R = \{ (u,v) | u^2 + v^2 \leq 4 \}. $$

Daí, usando a fórmula do cálculo de área de superfície, obtemos $$A = \int \int_{R}{dA} =  \int \int_{R}{| (1,0,4u) \wedge (0,1, 4v) | dudv} = $$ $$= \int \int_{R}{| (-4u, -4v, 1) | dudv} = \int \int_{R}{\sqrt{1+16(u^2 + v^2)} dudv}.$$

Usando coordenadas polares na integral dupla, encontramos $$A \int_{0}^{2 \pi} \int_{0}^{2}{\sqrt{1+16r^2}rdrd \theta}= \frac{65\sqrt{65} -1}{24} \pi \;\;\;u.a.$$

Leia Mais:

• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Várias Variáveis Reais a Valores Reais ou Campos Escalares
• EFEITO BORBOLETA | Edward Lorenz e a Teoria do Caos
• GRÁFICOS | Da Análise Estatística ao Mercado de Ações