Integral de Superfície | Campos Escalares, Campos Vetoriais e Fluxos

De certa forma, as Integrais de Superfície são generalizações das Integrais de Linha, pois a lógica é análoga. Se definimos as Integrais de Linha usando a parametrização de curvas, agora usaremos as parametrizações das superfícies. Até por isso, é importante que o leitor tenha um conhecimento prévio do estudo básicos das superfícies.

Leia Mais: Introdução às Superfícies: Parametrização, Suavidade e Cálculo de Área.

Além disso, as Integrais de Superfície também serão separadas entre as integrais de campos escalares sobre uma superfície e as integrais de campos vetoriais. No meio do artigo queremos falar sobre duas interpretações físicas de cada uma das formas das Integrais de Superfícies.

A Integral de Superfície de um Campo Escalar

A integral de superfície de f(x,y,z) sobre a superfície \mathbb{S} é dada por $$\int\limits_{\mathbb{S}}\int{f(x,y,z) dS}.$$ Se \mathbb{S} é dada em sua forma paramétrica r(u,v), então $$\int\limits_{\mathbb{S}}\int{f(x,y,z) dS}= \int\limits_{R}\int{f(x(u,v),y(u,v),z(u,v))\left\|\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\| dudv},$$ sendo R a região de domínio da superfície \mathbb{S}.

Por outro lado, se \mathbb{S} é dada em sua forma explícita z=g(x,y), então $$\int\limits_{\mathbb{S}}\int{f(x,y,z) dS}= \int\limits_{R}\int{f(x,y,g(x,y))\sqrt{1+\left( \frac{\partial g}{\partial x}\right)^2 + \left( \frac{\partial g}{\partial y}\right)^2}dxdy}.$$ Se a superfície é suave por partes então a integral de superfície é definida como a soma das integrais sobre cada pedaço suave da superfície.

Leia Mais: O que é uma curva suave por partes?

EXEMPLO

Calcule \int\limits_{\mathbb{S}}\int{(z-x^2+xy^2-1)dS}, onde $$\mathbb{S}:\vec{r} (u,v) = (u,v,u^2 +1); \;\; 0 \leq u \leq 2 \;\; e \;\; 0 \leq v \leq 5.$$

Neste caso, $$\int\limits_{\mathbb{S}}\int{(z-x^2+xy^2-1)dS} = \int\limits_{R}\int{(u^2+1-u^2+uv^2-1) \sqrt{4 u^2} dudv}=$$ $$= \int\limits_{0}^{5}\int\limits_{0}^{2}{(uv^2) \sqrt{4 u^2 +1} dudv} = \frac{1}{12}(17 \sqrt{17} -1) \int\limits_{0}^{5}{v^2 dv} = \frac{125}{36}(17 \sqrt{17} -1)$$

EXEMPLO

Calcule \int\limits_{\mathbb{S}}\int{x^2 z dS}, onde S é a porção do cone z^2 = x^2+y^2 que está entre os planos z=1 e z=4 .

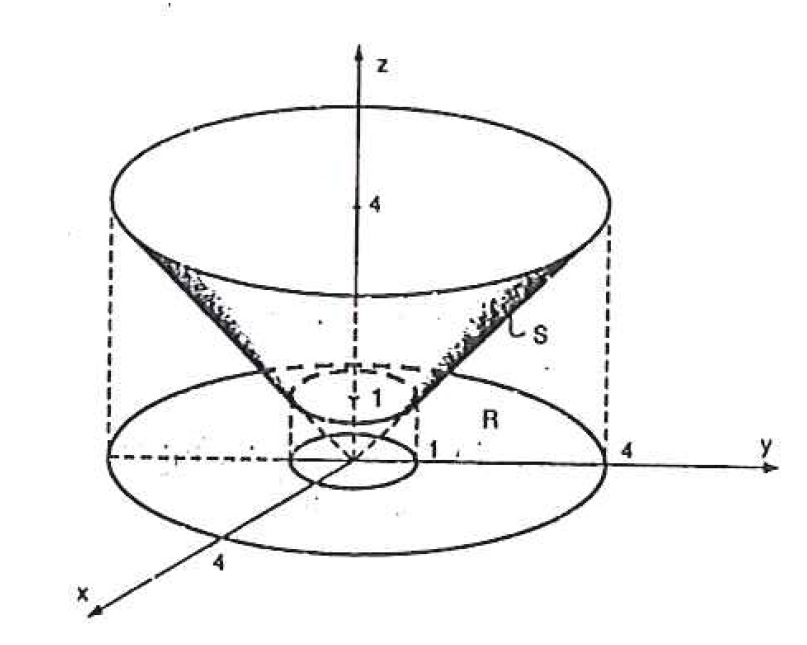
Usando coordenadas polares encontramos: $$\int\limits_{\mathbb{S}}\int{x^2 z dS} = \int\limits_{R}\int{x^2 \sqrt{x^2 +y^2} \sqrt{1 + \frac{x^2}{x^2 + y^2} +\frac{y^2}{x^2 + y^2} } dxdy}=$$ $$= \sqrt{2} \int\limits_{R}\int{x^2 \sqrt{x^2 +y^2} dxdy} = \frac{1023 \sqrt{2}}{5} \pi.$$

Uma situação mais geral ocorre quando a superfície não pode ser escrita por meio de uma única função x=x(y,z) , y=y(x,z) e z =z(x,yz) . São casos imediatos desta situação as esferas, elipsoides, cubos  ou quaisquer superfícies fechadas.

Este caso não oferece maior dificuldade, desde que se possa decompor a superfície em várias partes. Então a integral sobre cada uma das partes pode-se exprimir como a integral sobre o domínio conveniente de um dos planos coordenados. A integral sobre a superfície será a soma de todas estas integrais.

EXEMPLO

Calcule $$\int\limits_{\mathbb{S}}\int{(x+y+z)dS}$$, onde a superfície é a representada na figura abaixo:

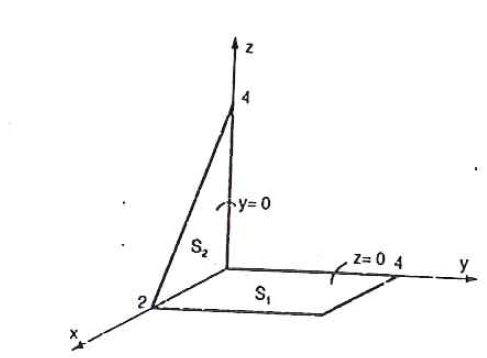
Como a superfície nesse caso e suave por partes, então integral de superfície será calculada somando as integrais sobre a primeira e a segunda superfície. Ou seja, $$\int\limits_{\mathbb{S}}\int{(x+y+z)dS} = \int\limits_{\mathbb{S}_1}\int{(x+y+z)dS} + \int\limits_{\mathbb{S}_2}\int{(x+y+z)dS}=$$ $$ = \int\limits_{0}^{4}\int\limits_{0}^{2}{(x+y+0)\sqrt{1+0+0}dxdy} + \int\limits_{0}^{2}\int\limits_{0}^{4-2x}{(x+0+z)\sqrt{1+0+0}dxdz} = $$ $$= \int\limits_{0}^{4}\int\limits_{0}^{2}{(x+y)dxdy} + \int\limits_{0}^{2}\int\limits_{0}^{4-2x}{(x+z)dzdx} = 24+8=32.$$

Observe que para calcular a integral sobre a segunda superfície tivemos que ajustar nossa fórmula para o cálculo da Integral de Superfície. Como, neste caso, a superfície é representada explicitamente por y = y(x,z) , então usamos a seguinte fórmula:

$$\int\limits_{\mathbb{S}}\int{f(x,y,z) dS}= \int\limits_{R}\int{f(x,y(x,z),z)\sqrt{1+\left( \frac{\partial g}{\partial x}\right)^2 + \left( \frac{\partial g}{\partial z}\right)^2}dxdz}$$, onde R é exatamente a projeção de S sobre o plano xz, nesse caso, o triângulo que forma a segunda parcela da superfície.

CENTRO DE MASSA E MOMENTO DE INÉRCIA

O centro de massa e o momento de inércia de uma lâmina podem ser calculados usando-se integrais de superfície. Supondo que S represente a lâmina e que o campo escalar represente  densidade (ou seja, a massa por unidade de área) em cada ponto desa lâmina, então a massa m da lâmina é dada por $$m = \int\limits_{\mathbb{S}}\int{f(x,y,z) dS}$$ e o centro de massa será o ponto (\bar{x}, \bar{y}, \bar{z}) , onde $$\bar{x} = \frac{1}{m} \int\limits_{\mathbb{S}}\int{xf(x,y,z) dS}$$ $$\bar{y} = \frac{1}{m} \int\limits_{\mathbb{S}}\int{y f(x,y,z) dS}$$ $$\bar{z} = \frac{1}{m} \int\limits_{\mathbb{S}}\int{z f(x,y,z) dS}.$$

Já o momento de inércia I_L de S em relação a um eixo L é dado por $$ \int\limits_{\mathbb{S}}\int{[\delta (x,y,z)]^2f(x,y,z) dS}$$ onde \delta (x,y,z) é a distância do ponto (x,y,z) de S  até o eixo L.

INTEGRAL DE SUPERFÍCIE DE UM CAMPO VETORIAL

Assim como a Integral de Linha de um campo vetorial depende da orientação da curva, de forma análoga, a integral de superfície de um campo vetorial dependerá do lado da superfície escolhido para a integração. Até por isso, todas a superfícies escolhidas nesse artigo serão consideradas orientáveis.

Considere uma  superfície suave \mathbb{S}, representada por $$\vec{r}(u,v) = x(u,v)\vec{i} + y(u,v)\vec{j} + z(u,v)\vec{k},$$ com (u,v) \in R e \vec{n} = \vec{n} (u,v) um vetor unitário normal a \mathbb{S}.

Seja \vec{F} um campo vetorial definido sobre \mathbb{S}, a Integral de Superfície de \vec{F} sobre \mathbb{S} é denotada por $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} = \int\limits_{R}\int{\vec{F}(x(u,v), y(u,v), z(u,v)) . \vec{n} (u,v) \left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\| dudv} .$$

Como temos duas direções diferentes para os vetores normais unitários da superfície, então $$\vec{n} = \pm \frac{\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v}}{\left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\|}.$$ Assim, a Integral de Superfície fica: $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} = \pm \int\limits_{R}\int{\vec{F}(x(u,v), y(u,v), z(u,v)) . \left(\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right) dudv} .$$ O sinal da integral ira depender de qual será escolhido como o vetor normal unitário da superfície.

EXEMPLO

Vamos calcular \int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} sendo \vec{F} (x,y,z) = (x,y,z) onde {\mathbb{S}} é a superfície exterior da esfera representada por r(u,v) = (a\cos{u}\cos{v})\vec{i} + (a\sin{u}\cos{v})\vec{j} + (a\sin{v})\vec{k},
onde 0\leq u \leq 2\pi e - \frac{\pi}{2} \leq v \leq \frac{\pi}{2}.

Primeiramente, observe que $$\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v}  = \left( a^2cos(u)cos^2(v), a^2 sen(u) cos^2(v), a^2 sen(v) cos(v) \right).$$

Esse é o vetor positivo que aponta para fora da esfera (como vimos nesse artigo), o que se encaixa no lado da superfície escolhido para integração. Logo,

$$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} =+ \int\limits_{R}\int{\vec{F}(x(u,v), y(u,v), z(u,v)) . \left(\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right) dudv} =$$ $$ = \int\limits_{R}\int{ (x(u,v), y(u,v), z(u,v)) . \left( a^2cos(u)cos^2(v), a^2 sen(u) cos^2(v), a^2 sen(v) cos(v) \right)dudv} = $$ $$ = \int\limits_{R}\int{ (a\cos{u}\cos{v} , a\sin{u}\cos{v}, a\sin{v} )}. $$ $$\left( a^2cos(u)cos^2(v), a^2 sen(u) cos^2(v), a^2 sen(v) cos(v) \right)dudv = $$ $$= \int\limits_{R}\int{ (a^3\cos^3{u}\cos^3{v} + a^3\sin^2 {u}\cos^3 {v} + a^3 \sin^2 {v} \cos{v} ) dudv} = $$ $$= \int\limits_{R}\int{a^3 cos(v) dudv} = a^3 \int\limits_{0}^{2 \pi}\int\limits_{- \pi /2 }^{\pi /2}{cos(v) dvdu} = 4a^3 \pi .$$

EXEMPLO

Seja S a superfície exterior do parabolóide r(u,v) = \left( x, y, x^2 + y^2 \right), com (x,y) \in R, onde R = \{(x,y) | x^2 + y^2 \leq 4 \} . Vamos determinar \int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} sendo \vec{F} (x,y,z) = (3x,3y,-3z).

Observe que $$\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v}  = \left( -2x, -2y, 1 \right)$$ e o vetor normal unitário aponta para o interior do parabolóide como podemos ver abaixo:

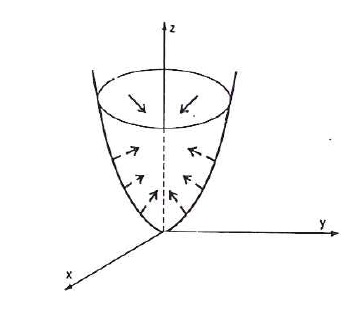
Como o lado escolhido para a integração é o lado exterior da superfície, nesse caso, a integral será $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} = -\int\limits_{R}\int{\vec{F}(x(u,v), y(u,v), z(u,v)) . \left(\frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right) dudv}.$$

Assim, ajustando as variáveis corretamente na fórmula acima e usando coordenadas polares, obtemos $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} = –  \int\limits_{R}\int{ \left(3x, 3y, -3 (x^2 + y^2) \right) . \left( -2x, -2y, 1 \right) dxdy} =$$ $$= 9 \int\limits_{R}\int{ (x^2 + y^2)dxdy} = 72 \pi .$$

FLUXO SOBRE A SUPERFÍCIE

A integral $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS}$$ aparece naturalmente em problemas de fluxo, onde ela nos dá o fluxo sobre a superfície, ou seja, a massa de fluido que passa pela superfície por unidade de tempo, quando  \vec{F} = \rho \vec{v} , sendo \rho a densidade do fluido e \vec{v} o vetor velocidade do fluxo.

Por isso, algumas vezes a Integral de Superfície é, também, chamada de Fluxo do Campo Vetorial Sobre a Superfície e se \vec{F} = (F_1, F_2, F_3) e \vec{n} = (n_1, n_2, n_3) , então $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} = \int\limits_{R}\int{(F_1 n_1+ F_2 n_2 + F_3 n_3) dudv} = $$ $$ = \int\limits_{\mathbb{S}}\int{(F_1 dydz + F_2 dzdx + F_3 dxdy)}.$$

Listas de Exercícios Resolvidos sobre Integrais de Superfície:

• Integral de Superfícies | 1ª Lista de Execícios Resolvidos

Leia Mais:

• Introdução às Superfícies: Parametrização, Suavidade e Cálculo de Área.
• Integral de Superfície | Teoremas de Stokes e da Divergência
• Integral Dupla | Teorema de Fubini, Exemplos e Exercícios Resolvidos
• Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano

Assista Nossa Vídeo-Aula Sobre Integrais de Superfície