Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula

Nesse artigo queremos desenvolver os conceitos de parametrização, comprimento de arco e deslocamento de partícula ligados às curvas no espaço. Uma função de uma variável a valores em \mathbb{R}^n é uma função F:A \rightarrow \mathbb{R}^n, onde A é um subconjunto de \mathbb{R}.

Esta função é, por muitas vezes, denominada de função vetorial ou curva, pois a representação dada por \vec{F}(t) = x(t) \vec{i} + y(t) \vec{j} + z(t) \vec{k} é chamara de representação paramétrica da curva C, e t é chamado de parâmetro desta representação. Este tipo de representação é útil em várias aplicações, por exemplo, em mecânica on a variável t pode ser o tempo.

Curvas no Espaço

Comumente ma função de uma variável a valores no \mathbb{R}^n é denominada curva parametrizada. Assim, uma função $$f(t)=(x_1(t), x_2(t),…,x_n(t))\;\;\;\;t\in \mathbb{R}$$ é uma curva e as funções reais x_i(t),\; i=1,...,n, são as equações paramétricas da curva e t é chamado de parâmetro.

Porém, com mais acuidade matemática definimos como curva o conjunto de todos os pontos (x(t), y(t), z(t)) do espaço determinados por uma função vetorial de uma variável.

Outras formas de representar curvas no espaço são $$ \tag{1} \left\{ \begin{array}{lll} y & = & f(x) \\ z & = & g(x) \end{array} \right. $$ ou $$ \tag{2} \left\{ \begin{array}{lll} F(x,y,z) & = & 0 \\ G(x,y,z) & = & 0 \end{array} \right.$$ Na forma (2) de escrever uma curva, cada equação representa uma superfície, e a curva é a interseção destas duas superfícies.

Uma curva plana é uma curva que está contida em plano do espaço. Uma curva que não é plana é chamada de reversa.

EXEMPLO

São exemplos de curvas:

1. \vec{f} (t) = (2cos(t), 2 sen(t), 3t) denominada hélice circular no espaço;
2. \vec{r} (t) = (t, t^2,3), que é uma parábola sobre o plano z = 3.

Curva Suave

Para uma curva parametrizada \vec{f} (t) , ela é suave, ou regular, se \vec{f'} (t) \neq \vec{0} , \;\;\; \forall t \in I \subset \mathbb{R}. Geometricamente uma curva suave é caracterizada pela ausência de pontos angulosos.

Em cada um de seus pontos, a curva suave tem uma tangente única que varia continuamente quando se move sobre curva. Uma curva é suave por partes se puder ser dividida em um número finito de curvas suaves.

Por exemplo, as retas, circunferências, elipses e hélices são curvas suaves, enquanto triângulos, quadrados e ciclóides não são curvas suaves, mas sim suaves por partes.

Curvas Simples

Uma curva parametrizada \vec{f} (t) é fechada se \vec{f} (a) = \vec{f} (b) se \vec{f} (t) está definida para t \in [a,b]. Nesse sentido, uma curva pode ter muitas interseções; os pontos de interseções são chamados de pontos múltiplos da curva. Uma curva que não possui pontos múltiplos é chamada da curva simples.

As curvas abaixo são exemplo de curvas que não são são simples pois possuem pontos múltiplos:

Parametrização de Curvas Clássicas:

RETA

Uma reta r com equações paramétricas x(t) = x_1 +at;\;\;y(t) = y_1 +bt e z(t) = z_1 +ct, ou seja, que passa pelo ponto (x_1, y_1, z_1) na direção do vetor (a,b,c) é uma curva parametrizada no espaço \mathbb{R}^3.

CIRCUNFERÊNCIA:

Um circunferência C com centro em (0, 0) e raio r>0 é uma curva parametrizada como equações paramétricas dadas por $$x(t) = r cost\;\;\;\;y(t) = r \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$

Se a circunferência não está centrada na origem, mas no ponto (x_0, y_0) e ainda com raio r>0, então sua parametrização será dada por $$x(t) = x_0 + r cost\;\;\;\;y(t) = y_0 + r \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$

ELIPSE

Vamos parametrizar a elipse dada por $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$ Inspirados pela relação $$\cos^2{t}+\sin^2{t}=1$$ temos que
\begin{eqnarray}
x & = & a\cos{t}\\
y & = & b\sin{t} \;\;\;\;\;\;\;\;\;\;\;\;\;t\in[0,2\pi]
\end{eqnarray}

Analogamente ao que fizemos com a circunferência, se a elipse não está centrada na origem, mas no ponto (x_0, y_0) e ainda tem seus eixos na direção dos eixos coordenados, então sua parametrização será dada por $$x(t) = x_0 + a cost\;\;\;\;y(t) = y_0 + b \sin{t} \;\;\;\;\;t \in [0, 2 \pi ].$$

Para encontrar mais parametrização de curvas clássicas leia este nosso artigo: Curvas no Espaço | Parametrização de Curvas Clássicas

Curvas Orientadas

Se um ponto material desloca-se sobre uma curve suave C, temos dois possíveis sentidos de percurso. A escolha de um deles como sentido positivo, define uma orientação na curva C.

Suponhamos que a curva C seja representada por f(t)=(x(t), y(t),z(t)); t \in [a,b] , convencionamos chamar de sentido positivo sobre C, o sentido no qual a curva é traçada quando o parâmetro t cresce da a até b. O sentido oposto é chamado de sentido negativo sobre C.

Por esta definição, o sentido positivo de uma curva orientada é o sentido dos valores crescentes do parâmetro t.

Se uma curva simples C é suave por partes, podemos orientá-la orientando cada parte suave de C como mostram as figuras abaixo:

Dada uma curva orientada C, representada por f(t)=(x(t), y(t),z(t)); t \in [a,b] , então definimos a curva -C como a curva C, mas com a orientação oposta. Nesse sentido, a curva -C é dada por $$ f^{-} (t) = f(a+b -t)=(x(a+b -t), y(a+b -t),z(a+b -t)); t \in [a,b].$$

EXEMPLO

Vamos parametrizar a circunferência de centro na origem e raio a no sentido horário.

Observe que no sentido horário a circunferência tem uma orientação oposta àquela que segue o crescimento de t \in [0, 2 \pi] .

Ou seja, queremos parametrizar -C, onde C é a circunferência.

Assim, como C: f(t)=(acos(t), a sen(t)); t \in [0, 2 \pi] , então $$-C: f^{-} (t) = f(0 + 2 \pi -t) = f(-t+2 \pi) = (acos(-t+2 \pi), a sen(-t+2 \pi)); t \in [0, 2 \pi]$$

Observando que as funções cosseno e seno são 2 \pi -periódicas e funções par e ímpar, respectivamente, ficamos com $$-C: f^{-} (t) = (acos(t), -a sen(t)); t \in [0, 2 \pi]$$

A imagem abaixo ilustra o exemplo:

Comprimento de Arco

Seja f(t)=(x_1(t), x_2(t),...,x_n(t))\;\;\;\;a\leq t \leq b uma curva contínua em [a,b]. O comprimento de arco desta curva no espaço é dado por $$ s=\int_{a}^{b}{\left\| f'(t) \right\| } dt .$$

À partir desta definição podemos definir a função comprimento de arco, que mede o comprimento da curva no intervalo [a,b] da seguinte forma: $$ s(t) = \int_{a}^{t}{\left\| f'( \tau ) \right\| } d \tau  .$$ A constante a neste caso seria o ponto inicial da curva . O sentido correspondente ao crescimento do parâmetro é denominado sentido positivo da curva e com isso podemos definir uma orientação do caminho.

Além disso,  lembrando que a norma cartesiana provém de um produto interno, $$ s(t) = \int_{a}^{t}{\left\| f'( \tau ) \right\| } d \tau =  \int_{a}^{t}{ \sqrt{f'( \tau ) \cdot f'( \tau ) } } d \tau.$$ Daí, $$ \left( \frac{d s}{dt} \right)^2 = \frac{d\vec{f}}{dt} \cdot \frac{d\vec{f}}{dt} = \left( \frac{dx}{dt} \right) ^2 + \left( \frac{dy}{dt} \right) ^2 + \left( \frac{dz}{dt} \right) ^2 .$$

Geralmente escrevemos $$ d \vec{r} = dx \vec{i} + dy \vec{j} + dz \vec{k}$$ e $$ ds^2 = d \vec{r} \cdot d \vec{r} = dx^2 + dy^2 +dz^2.$$

EXEMPLO

Calcule o comprimento da hélice circular f(t)=\left( \cos{t}, \sin{t}, t \right), t \in [0, 2 \pi].

1. f'(t)=\left( -\sin{t}, \cos{t}, 1 \right);
2. \|f'(t)\|=\|\left( -\sin{t}, \cos{t}, 1 \right)\|=\sqrt{2};
3. s=\int_0 ^{2\pi}{\|f'(t)\|}dt = 2\pi \sqrt{2}.

EXEMPLO

Calcule o comprimento da circunferência de raio R>0.

Sabemos que essa circunferência pode ser parametrizada pela curva $$C(t)=(R\cos{t}, R\sin{t}).$$

O comprimento da circunferência é C(2\pi). De fato,

\begin{eqnarray*}
C(2\pi) & = & \int_0 ^{2\pi}{\sqrt{R^2\sin^2{t} +R^2\cos^2{t}}}dt\\
& = & \int_0 ^{2\pi}{\sqrt{R^2}}dt\\
& = & \int_0 ^{2\pi}{R}dt\\
& = & 2\pi R
\end{eqnarray*}

EXEMPLO

Escreva a função comprimento de arco da circunferência de raio R>0.

Usando a lógica do exemplo anterior temos que

\begin{eqnarray*}
s(t) & = & \int_0 ^{t}{\sqrt{R^2\sin^2{ \tau } +R^2\cos^2{ \tau }}}d \tau \\
& = & \int_0 ^{t}{\sqrt{R^2}}d \tau \\
& = & \int_0 ^{t}{R}d \tau \\
& = & R t
\end{eqnarray*}

EXEMPLO

Calcule o comprimento da curva \gamma (t) = \left( t\cos{t}, t\sin{t} \right) com t \in[0,2\pi].

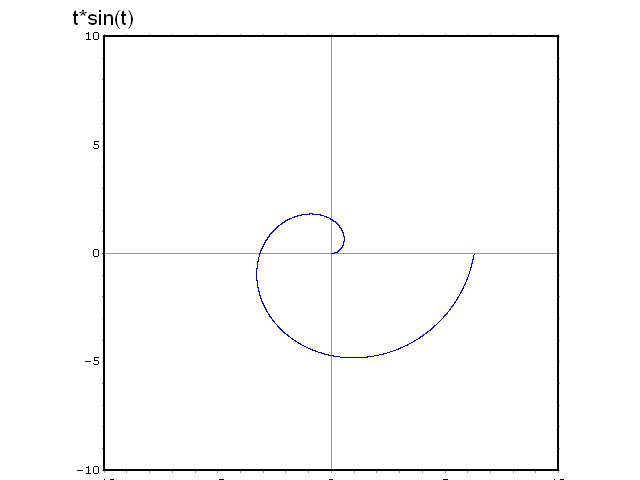
\begin{eqnarray*}
s & = & \int_0 ^{2\pi}{\sqrt{t^2\cos^2{t} +t^2\sin^2{t}}}dt\\
& = & \int_0 ^{2\pi}{\sqrt{t^2}}dt\\
& = & \int_0 ^{2\pi}{t}dt\\
& = & \frac{4\pi^2}{2}
\end{eqnarray*}

PARAMETRIZAÇÃO DE CURVAS PELO COMPRIMENTO DE ARCO

O comprimento de arco pode servir de parâmetro em uma representação paramétrica de curvas, e é conveniente parametrizarmos algumas curvas usando o comprimento de arco s, pois isso irá simplificar várias das fórmulas.

Para reparametrizarmos uma curva suava C, dada por f(t)=(x_1(t), x_2(t),...,x_n(t))\;\;\;\;a\leq t \leq b  procedemos como segue:

1. Calculamos s=s(t) ;
2. Encontramos a sua inversa t = t(s), 0\leq s \leq l;
3. Finalmente, reescrevemos f(t)=(x_1(t), x_2(t),...,x_n(t))\;\;\;\;a\leq t \leq b como $$ h(s) = f(t(s)) = (x_1(t), x_2(t),…,x_n(t))\;\;\;\;a\leq s \leq l .$$

Temos então, que h(s) descreve a mesma curva C que era dada por f(t), mas com uma nova parametrização, onde a variável s, a\leq s \leq l , representa o comprimento de arco de C.

É possível mostrar, e isso é um ótimo exercício, que dada uma curva C, representada por f(t), então | f' (t) | = 1 , se, e somente se, o parâmetro t é o parâmetro comprimento de arco de C.

EXEMPLO

Vamos reparametrizar pelo comprimento de arco a curva f (t) = \left(R \cos{t}, R \sin{t} \right) com t \in[0,2\pi].

A função comprimento de arco já foi calculada nos exemplos anteriores e é dada por $$s(t) = R t. $$

Esta função é uma função linear, cuja inversa é dada por $$t = t(s) = \frac{s}{R}, 0 \leq s \leq 2 \pi R.$$

Portanto $$h(s) = f(t(s)) = \left( R cos \left(\frac{s}{R} \right), R sen \left(\frac{s}{R} \right) \right) , 0 \leq s \leq 2 \pi R , $$ é a reparametrização da circunferência dada.

EXEMPLO

Vamos reparametrizar pelo comprimento de arco a curva f (t) = \left(e^t cos(t), e^t sen(t) \right) com t \geq 0.

Nesse caso, podemos encontrar a função comprimento de arco (deixo essa parte como exercício para o leitor) como $$s(t) = \sqrt{2} \left( e^t -1 \right) . $$

Podemos escrever $$ t = t(s) = \ln \left( \frac{s + \sqrt{2}}{\sqrt{2}} \right), s \geq 0.$$

Daí $$h(s) = \frac{s + \sqrt{2}}{\sqrt{2}} \left[ cos \left( \ln \left( \frac{s + \sqrt{2}}{\sqrt{2}} \right) \right), sen \left( \ln \left( \frac{s + \sqrt{2}}{\sqrt{2}} \right) \right) \right], s \geq o.$$

EXEMPLO

Verifique que a curva $$ f (s) = \left(\frac{s}{\sqrt{5}}, \frac{2s}{\sqrt{5}} \right) $$ com s \geq 0 está parametrizada pelo comprimento de arco.

Observe que $$f’ (s) = \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right)$$ $$|f’ (s)| = \sqrt{\left(\frac{1}{\sqrt{5}} \right) ^2, \left( \frac{2}{\sqrt{5}} \right) ^2} = \sqrt{1/5 + 4/5} = 1.$$

Portanto, a curva C dada tem como parâmetro o comprimento de arco.

Deslocamento de Uma Partícula

A função f(t) também pode ser referenciada como vetor posição, pois para cada instante t, f(t) denota a posição de f quando se trata do movimento de uma partícula. O vetor \vec{v} (t) = \vec{f'} (t) é a velocidade instantânea da partícula no tempo t, quando o limite que define esta derivada existe. Quando \vec{v} (t) admite derivada, então \vec{a} (t) = \vec{v'} (t) = \vec{f''} (t) será a aceleração da partícula.

Para entender mais sobre as curvas como trajetórias de partículas leia este nosso artigo: Curvas no Espaço | Deslocamento de Partícula

Leia Mais:

• Curvas no Espaço | Funções de uma Variável Real a Valores Vetoriais
• Curvas | Limite e Continuidade de uma Função Vetorial
• Curvas | A Derivada de Funções Vetoriais
• Curvas no Espaço | 1ª Lista de Exercícios Resolvidos

Assista nossa Vídeo-Aula: