O que são Conjuntos Numéricos? Dos Naturais aos Complexos.

Damos o nome de conjuntos numéricos a certos conjuntos cujos elementos são números que guardam entre si alguma característica em comum. Tais conjuntos possuem os elementos perfeitamente caracterizados e surgiram como ampliações dos conjuntos previamente estabelecidos à partir da necessidade de se contar objetos.

A base de todo o estudo do Cálculo Diferencial e Integral será tomada no conjunto dos números reais. Este conjunto é construído a partir de alguns subconjuntos que pode exemplificar de maneira simples as relações de pertinência e inclusão.

Os Conjuntos Numéricos

NÚMEROS NATURAIS: O conjunto dos números naturais é indicado por \mathbb{N} e é formado pelos elementos $$0,1,2,3,4,5,6,7,8,9,10,…$$ Este conjunto é infinito e limitado inferiormente, ou seja, ele possui um primeiro elemento que é o 0. Sendo assim, sabemos que 1 é um elemento de \mathbb{N} e indicamos tal relação por $$1 \in \mathbb{N}.$$ Por outro lado, sabemos que o elemento -10 não pertence ao conjunto \mathbb{N} e indicamos isso pela relação $$-10 \notin \mathbb{N}.$$

Em análise, o conjunto dos números naturais \mathbb{N} é caracterizado pelos chamados Aximomas de Peano:

1. Todo número natural possui um sucessor que ainda é um número natural e números naturais diferentes possuem sucessores diferentes.
2. Existe um único natural 1 que não é sucessor de nenhum outro natural.
3. PRINCÍPIO DA INDUÇÃO: Todo número natural pode ser obtido a partir de 1.

NÚMEROS INTEIROS: O conjunto dos números inteiros é aquele formado por números positivos, negativos e o zero, mas não admite frações ou números decimais que não possam ser escritos em forma de fração. Este conjunto é indicado por \mathbb{Z} e tem como elementos $$…-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,…$$ Podemos perceber que este conjunto é infinito e ilimitado, ou seja, não possui um primeiro ou um último elemento e ainda que o conjunto \mathbb{N} é um subconjunto de \mathbb{Z}, pois cada elemento dos números naturais é um elemento dos números inteiros, ou seja, $$\mathbb{N} \subset \mathbb{Z}$$. Algumas vezes o conjunto dos números naturais é referenciado como conjunto dos números inteiros não negativos.

NÚMEROS RACIONAIS: Denominamos ao conjunto $$\mathbb{Q}=\left\{ q=\frac{m}{n}; m,n \in \mathbb{Z}\;\;\;e\;\;\;mdc(m,n)=1 \right\}$$ de conjunto dos números racionais. Este conjunto é conhecido como o conjunto das frações e dos números decimais que podem ser escritos como fração. Note que todo números inteiro pode ser escrito como uma fração se tomarmos o seu denominador como sendo 1. Sendo assim, obtemos a seguinte cadeia de desigualdades: $$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}$$

NÚMEROS IRRACIONAIS: Porém existem números que não podem ser escritos como uma fração, pois possuem infinitas casas decimais e não existem dois números inteiros cuja divisão resulte neles. Estes números são conhecidos como números irracionais e seu elementos são as raízes quadaradas de números primos, dízimas não periódicas, o número \pi que é a razão entre a medida da circunferência e o seu raio e o número \Phi conhecido como o número de ouro. Ou seja, são exemplos de números irracionais: $$\pi; \sqrt{2}; \sqrt{3};\;\;\; e \;\;\;1,414243444546474849… $$ Note que, nenhum número racional pertence ao conjunto dos números irracionais, assim podemos dizer que \mathbb{Q} não está contido no conjunto dos números irracionais. Na verdade, os dois conjuntos são denominados disjuntos, pois não pertencem nenhum elemento em comum.

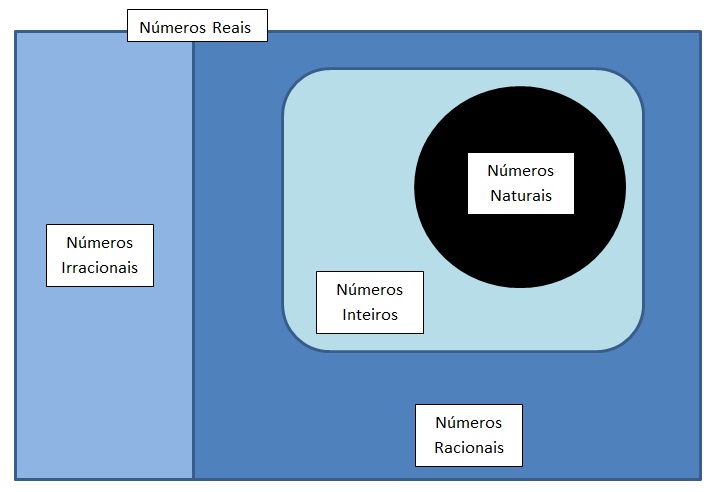
NÚMEROS REAIS: O conjunto dos números reais, indicado por \mathbb{R} é formado pela união dos conjuntos do números racionais com os números irracioais. Sendo assim, todo número que não seja resultado de um raíz de ordem par de um número negativo é um número real. Graficamente, podemos interpretar o conjunto dos números reais como dado na figura abaixo.

NÚMEROS COMPLEXOS: Um número complexo z é um par ordenado (x,y) de número reais x e y onde se escreve $$z=(x,y)$$ e denominamos x de parte real e y de parte imaginária de z e escrevemos $$x=Re(z)\;\;\;e\;\;\;y=Im(z).$$

O ponto (0,1) é denominado unidade imaginária e é denotado por i. Ou seja, $$i=(0,1).$$ Desta forma, (0,y) = y (0,1) = yi. De maneira análoga, podemos encarar (x,0) = x. Assim, $$(x,y) = (x,0)+(0,y) = x(1,0) + y(0,1) = x+iy.$$ Na prática, um número complexo z=(x,y) é representado na forma $$z=x+iy=Re(z)+Im(z) i$$ que é denominada forma cartesiana de z.

Na história da matemática, o primeiro a utilizar os números complexos foi o matemático italiano Girolando Cardano por volta do século XVI para solucionar equações cúbicas. Porém, foi Gauss, o maior matemático de todos os tempos, quem apresentou uma teoria consistente para os números complexos. Equações na forma x^2+1=0 são observadas desde os primórdios da matemática e elas deram origem ao que hoje chamado de número complexo.

Leia Mais:

• Números Racionais | Definição, Propriedades e Operações Elementares
• Números Complexos | Primeiras Definições e Operações Elementares
• Ajuste de Dados – Como fazer arredondamento de números?
• O que são Expressões Algébricas? | Matemática Básica