Integrais Triplas | 1ª Lista de Exercícios Resolvidos

As integrais triplas são o análogo de integrais duplas em três dimensões. Elas são uma ferramenta para somar infinitamente grandezas infinitesimais associadas a pontos em uma região tridimensional. Assim como para as integrais duplas, podemos também aplicar o teorema de Fubini generalizado e calcular as integrais triplas a partir disso.

A técnica utilizada para efetuarmos o cálculo da integral tripla é reduzi-la a uma integral dupla. O teorema de Fubini nos diz que a partir das integrais triplas, podemos representá-las através das integrais iteradas com três variáveis.

A ideia é a mesma para duas variáveis, com as incógnitas variando entre duas constantes, onde, sendo D o paralelepípedo x_0 \leq x \leq x_1; \;\;\; y_0 \leq y \leq y_1; \;\;\; z_0 \leq z \leq z_1 : $$ \iiint_{D}{f(x,y,z) dxdydz} = \int_{x_0}^{x_1}\int_{y_0}^{y_1} \int_{z_0}^{z_1}{f(x,y,z) dxdydz}.$$ Este procedimento será usado para resolver os execícios abaixo.

Lista de Exercícios Resolvidos sobre Integrais Triplas

1) Calcule \int\limits_{T} \int \int{f(x,y,z)dxdydz} onde:

(a) f(x,y,z) = x e T é o sólido delimitado pelo cilindro x^2+y^2=25, pelo plano xy e pelo plano x+y+z=8.

O sólido T pode ser visualizado na figura abaixo:

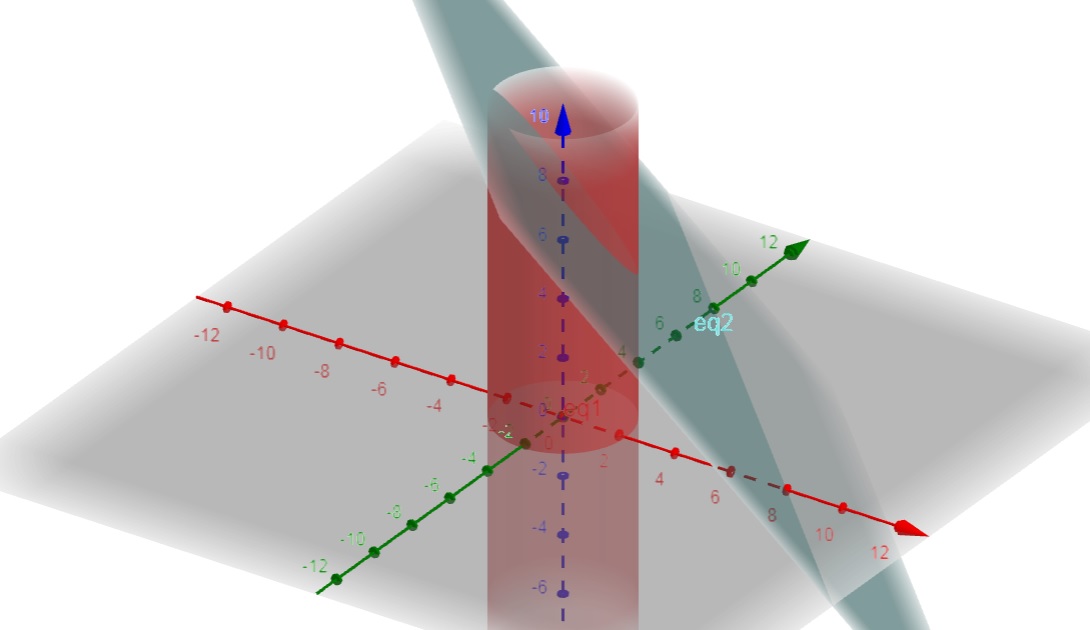
Assim, usando coordenadas cilíndricas, obtemos $$\int\limits_{T} \int \int{f(x,y,z)dxdydz} = \int_{0}^{2 \pi} \int_{0}^{5} \int_{0}^{8 – r (cos \theta + sen \theta)}{r^2 cos( \theta)dr d \theta dz}=$$ $$= \int_{0}^{2 \pi} \int_{0}^{5}(-r^3 cos \theta sen \theta – r^3 cos^2 \theta + 8r^2 cos \theta)dr d \theta = $$ $$ = \int_{0}^{2 \pi} (-1875cos \theta sen \theta – 1875 cos^2 \theta +4000 cos \theta)d\theta = \frac{-625 \pi}{8}$$

(b) f(x,y,z) = xyz^2 e T é o paralelepípedo [0,1]\times[0,2]\times[1,3].

Nesse caso, o sólido T sera escrito com suas variáveis entre constantes, que são os intervalos de cada uma das variáveis: $$ 0 \leq x \leq 1$$ $$0 \leq y \leq 2$$ $$1 \leq z \leq 3.$$

$$\int\limits_{T} \int \int{f(x,y,z)dxdydz} = \int_{0}^{1} \int_{0}^{2} \int_{1}^{3}{xyz^2 dzdydx} =$$ $$= \int_{0}^{1} \int_{0}^{2}{\frac{26}{3}xydydx} =  \int_{0}^{1} {\frac{53}{3}xdx} = \frac{26}{3}$$

(c) f(x,y,z) = \dfrac{1}{(x+y+z+1)^2} e T é o sólido delimitado pelos planos coordenados e pelo plano x+y+z=2

Observe, pela figura abaixo que o sólido delimitado pelos planos coordenados e pelo plano x+y+z=2 é o tetraedro com vértices (0,0,0), (0,0,2), (0,2,0)\;\;e\;\;(2,0,0).

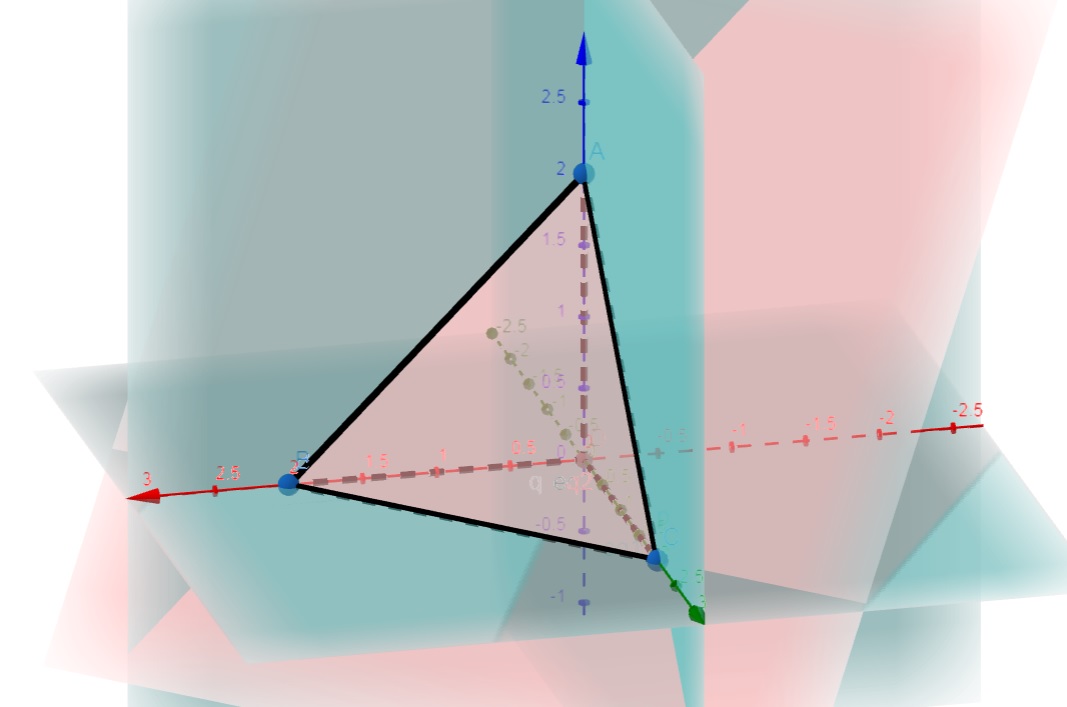
Nessa imagem, os planos esverdeados são os planos coordenados e o plano avermelhado é o plano x+y+z=2. Esse sólido T pode escrito como segue: $$0 \leq x \leq 2$$ $$0 \leq y \leq 2$$ $$0 \leq z \leq 2-x-y$$ Assim, $$\int\limits_{T} \int \int{f(x,y,z)dxdydz} = \int_{0}^{2} \int_{0}^{2} \int_{0}^{2-x-y}{\frac{1}{(x+y+z+1)^2}}dzdydx = $$ $$= \int_{0}^{2} \int_{0}^{2}{\left( \frac{1}{x+y+1} – \frac{1}{3} \right) dydx} = \int_{0}^{2} {\left( \ln{(x+y+1)} – \frac{y}{3} \right)_{0}^{2} dx} = $$ $$= – \int_{0}^{2} {\left( \ln{(x+3)} – \frac{2}{3} – \ln{(x+1)} \right)dx}= -\ln{\left( \frac{3125}{729} \right)} +\frac{4}{3}$$

(d) f(x,y,z) = x+y+z e T é o domínio delimitado por 0 \leq x \leq 1, 0 \leq y \leq 1 e 0 \leq z \leq 1 .

SOLUÇÃO: Neste caso estamos integrando sobre um sólido T que é um cubo dado por 0 \leq x \leq 1, 0 \leq y \leq 1 e 0 \leq z \leq 1 . Logo, $$\int \int \int\limits_{T}{f(x,y,z)dxdydz} = \int\limits_{0}^{1} \int \limits_{0}^{1} \int\limits_{0}^{1}{(x+y+z)dxdydz} = $$ $$= \int\limits_{0}^{1} \int \limits_{0}^{1}{\left( z+y+\frac{1}{2} \right)dydz} =  \int \limits_{0}^{1}{\left( z+1 \right)dz} = \frac{3}{2}.$$

(e) f(x,y,z) = xyz e T é o tetraedro delimitado pelos planos coordenados e pelo plano e x+y+z = 1.

SOLUÇÃO: Neste caso nosso sólido T é o tetraedro dado por $$T: \left\{ \begin{array}{l} 0 \leq x \leq 1\\ 0 \leq y \leq 1 – x\\ 0 \leq z \leq 1- x-y\end{array} \right.$$ Desta forma $$\int \int \int\limits_{T}{f(x,y,z)dxdydz} = \int\limits_{0}^{1} \int \limits_{0}^{1-x} \int\limits_{0}^{1-x-y}{xyzdzdydx} = $$ $$ =  \int\limits_{0}^{1} \int \limits_{0}^{1-x} {\frac{x\,y\,{\left( y+x-1\right) }^{2}}{2}dydx} = \int\limits_{0}^{1}{\frac{{\left( x-1\right) }^{4}\,x}{24}dx} = \frac{1}{720}$$

2) Se T é um sólido descrito por $$0 \leq x \leq 1$$ $$0 \leq y \leq x^2$$ $$0 \leq z \leq x+y $$ calcule $$ \iiint\limits_{T}{(2x-y-z)dxdydz}$$

SOLUÇÃO: $$ \iiint_{T}{(2x-y-z)dxdydz} = \int\limits_{0}^{1}\int\limits_{0}^{x^2}\int\limits_{0}^{x+y}{(2x-y-z)dzdydx} = $$ $$ = \frac{3}{2}\int\limits_{0}^{1}\int\limits_{0}^{x^2}{(x^2 – y^2)dydx} = \frac{3}{2}\int\limits_{0}^{1}{(x^4 – \frac{x^6}{3})dx} = \frac{8}{35}$$

Leia Mais:

• As Integrais Triplas | Definição, Exemplos e Exercícios Resolvidos
• Mudança de Variável em Integrais Triplas | Coordenadas Cilíndricas e Esféricas
• Como Calcular Volumes e Áreas com Integrais Múltiplas?
• Integrais Duplas Impróprias | Teoria e Exercícios Resolvidos.

Assista Nossa Vídeo-Aula Sobre Integrais Triplas: