Números Racionais | Definição, Propriedades e Operações Elementares

Em matemática, um número racional é um tipo de número real, que está na forma de p/q,  onde q não é igual a zero. Qualquer fração com denominadores diferentes de zero é um número racional. Neste artigo estudaremos os números racionais com vistas a aplicações no Cálculo Diferencial e Integral.

Indicamos por \mathbb{N}, \mathbb{Z} e \mathbb{Q} os conjuntos dos números naturais, inteiros e racionais respectivamente. Assim $$\begin{array}[t]{l}\mathbb{N} = \{ 0,1,2,3,\ldots\} ,\\
\mathbb{Z} = \{ \ldots,-3,-2,-1,0,1,2,3,\ldots\}, \\ \mathbb{Q} = \left\{
\frac{a}{b}; a,b\in \mathbb{Z},b\neq 0\right\}.
\end{array}$$

A soma e o produto em \mathbb{Q} são dados, respectivamente, por:
$$ \begin{array}{l} \frac{a}{b} + \frac{c}{d} :=
\frac{ad+bc}{bd}\\
\frac{a}{b} \cdot \frac{c}{d} := \frac{ac}{bd},.
\end{array}$$

Chamamos adição a operação que a cada par (x,y)\in \mathbb{Q} \times \mathbb{Q}associa sua soma x+y\in \mathbb{Q} e chamamos multiplicação a
operação que a cada par (x,y)\in \mathbb{Q}\times\mathbb{Q} associa seu produto x\cdot y\in \mathbb{Q}.

A terna (\mathbb{Q},+,\cdot), ou seja, \mathbb{Q} munido das operações “,+,”, e “\;\cdot\;”, satisfaz as propriedades de um
corpo. Isto quer dizer que valem as propriedades seguintes:

• (A1) (associativa) (x+y)+z=x+(y+z), para quaisquer x,y,z\in \mathbb{Q};
• (A2) (comutativa) x+y = y+x, para quaisquer x,y\in\mathbb{Q};
• (A3) (elemento neutro) existe 0\in \mathbb{Q} tal que x+0=x, para todo x\in\mathbb{Q};
• (A4) (elemento oposto) para todo x\in\mathbb{Q}, existe y\in\mathbb{Q}\;(y=-x), tal que x+y=0;
• (M1) (associativa) (xy)z=x(yz), para quaisquer x,y,z\in\mathbb{Q};
• (M2) ( comutativa) xy=yx, para todo x,y\in\mathbb{Q};
• (M3) (elemento neutro) existe 1\in\mathbb{Q}, tal que x1=x, para todo x\in\mathbb{Q};
• (M4) (elemento inverso) para todo x\in\mathbb{Q}, \ x\neq 0, existe y\in Q, \left( y = \frac{1}{x}\right), tal que x\cdot y=1;
• (D) (distributiva da multiplicação) x(y+z)=xy+xz, \ \forall \ x,y,z\in\mathbb{Q} .

Apenas com estas 9 propriedades podemos provar todas as operações algébricas com o corpo \mathbb{Q}. Vamos enunciar algumas e demonstrar outras a seguir.

[Lei do Cancelamento]: Em \mathbb{Q}, podemos afirmar que x+z=y+z \Rightarrow x=y.

Prova: $$x+z =  y+z \Rightarrow (x+z)+(-z) = (y+z)+(-z) \Rightarrow $$ $$ \Rightarrow x+(z-z) = y+(z +(-z)) \Rightarrow $$ $$\Rightarrow x+0=y+0 \Rightarrow x=y. $$

As seguintes proposições seguem da Lei do Cancelamento:

1. O elementos neutros da adição e da multiplicação são únicos.
2. O elemento oposto e o elemento inverso são únicos.
3. Para todo x\in \mathbb{Q}, x\cdot 0=0.
4. Para todo x\in \mathbb{Q}, -x = (-1) x.

Números Pares e Ímpares:

“Número par é todo o número que pode ser dividido em duas partes iguais sem que uma unidade fique no meio. Já número ímpar são aqueles números que não podem ser divididos em duas partes iguais, isso porque sempre haverá um número no meio.”

A “definição algébrica” usada para reconhecer os números pares é: dado um número p, pertencente ao conjunto dos números inteiros, p será par se: p = 2n. Já os números ímpares seriam na forma: p = 2n+1. Nesse caso, n é um elemento do conjunto dos números inteiros.

Os números pares e ímpares carregam propriedades interessantes como:

1. Entre dois números ímpares consecutivos sempre existe um número par.
2. Entre dois números pares consecutivos sempre existe um número ímpar.
3. A soma entre dois números inteiros consecutivos sempre será um número ímpar.
4. A soma de dois números pares ou dois números ímpares, sempre será um número par.

Números Racionais Positivos e Negativos; Desigualdades

Diremos que \frac{a}{b},\in\mathbb{Q} é:

1. não-negativo, se a\cdot b\in \mathbb{N};
2. positivo, se a\cdot b\in \N e a\neq 0
3. não-positivo, se \frac{a}{b} não for positivo;
4. negativo, se \frac{a}{b} não for não-negativo.

Sejam x,y\in\mathbb{Q}. Diremos que x é menor do que y e escrevemos x<y, se existir t\in\mathbb{Q} positivo tal que $$y=x+t.$$ Neste mesmo caso, poderemos dizer que y é maior do que x e escrevemos y>x. Em particular, teremos x>0 se x for positivo e x<0 se x for negativo.

Se x<y ou x=y, então escreveremos x\leq y e lemos “x é menor ou igual a y”. Da mesma forma, se y>x ou y=x, então escreveremos y\geq x e, neste caso, lemos “y é maior ou igual a x”. Escreveremos x\geq 0 se x for não-negativo e x\leq 0 se x for não-positivo.

A quádrupla (,\mathbb{Q},+,\ \cdot, \ ,\leq,) satisfaz as propriedades de um corpo ordenado, ou seja, além das propriedades anteriores, também valem as propriedades seguintes:

• (O1) (reflexiva) x\leq x, para todo x\in\mathbb{Q};
• (O2) (anti-simétrica) x\leq y e y\leq x  \Longrightarrow x=y, para quaisquer x,y\in\mathbb{Q};
• (O3) ( transitiva) x\leq y, \ y\leq z \Longrightarrow x\leq z, para quaisquer x,y,z\in\mathbb{Q};
• (O4) Para quaisquer x,y\in\mathbb{Q}, \ x\leq y  ou y\leq x;
• (OA) x\leq y \Longrightarrow x+z\leq y+z;
• (OM) x\leq y e z\geq 0 \Longrightarrow xz \leq yz.

Para quaisquer x,y,z,w no corpo ordenado \mathbb{Q}, valem:

• \begin{array}{l} x\leq y\\ z\leq w \end{array} \biggr\}\Longrightarrow x+z\leq y+w.
• \begin{array}{l} 0\leq x\leq y\\ 0\leq z\leq w\end{array}\biggr\} xz \leq yw.

Prova: Vamos provar o ítem (b).

$$ \begin{array}{l} 0\leq x \leq y \\
0 \leq z \leq w \end{array}\biggr\} \ \Rightarrow\
\begin{array}{l} xz \leq yz\\ yz\leq yw
\end{array}\biggr\} \ \Rightarrow \ xz \leq yw $$

Outras propriedades dos Números Racionais

Sejam x,y,z,w\in \mathbb{Q}. Então valem

• x<y \Longleftrightarrow x+z< y+z;
• z>0 \Longleftrightarrow  \frac{1}{z}>0;
• z>0 \Longleftrightarrow -z < 0;
• Se z>0, então x<y \Longleftrightarrow xz < yz;
• Se z<0, então x<y \Longleftrightarrow xz > yz;
• \left\{ \begin{array}{l} 0\leq x < y\\ 0\leq z < w \end{array} \right. \Rightarrow xz < yw;
• 0<x<y \Longleftrightarrow 0<\frac{1}{y}<\frac{1}{x};
• (Lei da Tricotomia)  x<y ou x=y ou x>y;
• (anulamento do produto) xy=0 \Longleftrightarrow x=0 ou y=0.

Nem Todo Número é Racional.

Os números racionais podem ser representados por pontos em uma reta horizontal ordenada, chamada reta real.

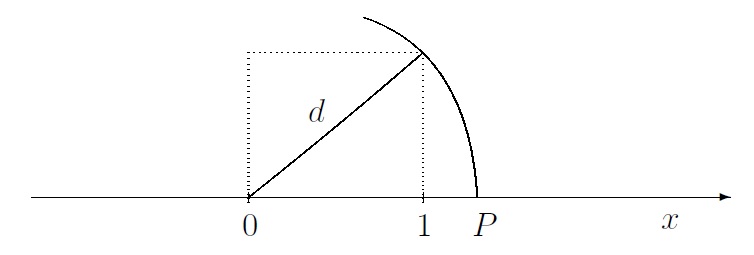
Se P por a representação de um número racional x, diremos que x é a abscissa de P. Nem todo ponto da reta real é racional. Considere um quadrado de lado 1 e diagonal d. Pelo Teorema de Pitágoras,
$$d^2=1^2+1^2=2.$$

Seja Pa intersecção do eixo x com a circunferência de raio d, como na figura abaixo, é possível mostrar que P é um ponto da reta com abscissa x\not\in\mathbb{Q}.

Leia Mais:

• Uma Breve História do Cálculo Diferencial e Integral
• Desafios de Matemática: Alguns problemas para desafiar sua mente!
• Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
• O que são Expressões Algébricas? | Matemática Básica