PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Em Geometria Analítica associamos a circunferência a uma equação à partir de sua definição e, daí, podemos extrair analiticamente todas as suas propriedades.
Neste artigo vamos explorar as equações e posições relativas envolvendo circunferências. Seja por sua presença e a aplicação no cotidiano ou por sua utilização em Matemática, a circunferência é uma figura bastante familiar para nós.

A circunferência é o lugar geométrico dos pontos de um plano que estão a uma mesma distância r de um ponto C fixado, chamado centro da circunferência.
Isso significa que se um ponto qualquer P(x,y) movimentar-se sobre a circunferência, suas coordenadas variarão, mas a distância de P(x,y) ao centro da circunferência será sempre igual à medida do raio.
Os 5 Melhores Livros Sobre Geometria Analítica
- “Geometria Analítica: Um Tratamento Vetorial”, de Paulo Boulos e Ivan De Camargo.
- “Geometria Analítica”, de Alfredo Steimbruch e Paulo Winterle
- “Fundamentos de matemática elementar – Volume 7: Geometria analítica”, de Gelson Iezzi.
- “Coordenadas No Plano”, de Elon Lages Lima.
- “Coordenadas no Espaço”, de Elon Lages Lima.
A Equação Reduzida da Circunferência
Uma circunferência com centro C \left( x_C , y_C \right) e raio r é o conjunto de todos os pontos P \left( x , y \right) do plano que distam r de C , ou seja: $$d_{PC} = \sqrt{ \left(x-x_C \right)^2+ \left(y-y_C \right)^2 } = r $$ Elevando membro a membro ao quadrado, temos: $$ \left(x-x_C \right)^2+ \left(y-y_C \right)^2 = r^2, $$ que é chamada de equação reduzida da circunferência, em que:
- x_C e y_C são coordenadas do centro C da circunferência;
- r é o raio da circunferência;
- x e y são as coordenadas do ponto genérico P – um ponto que pode ocupar o lugar de qualquer ponto da circunferência, sempre distando r de C
Todos estes elementos podem ser vistos na figura abaixo:
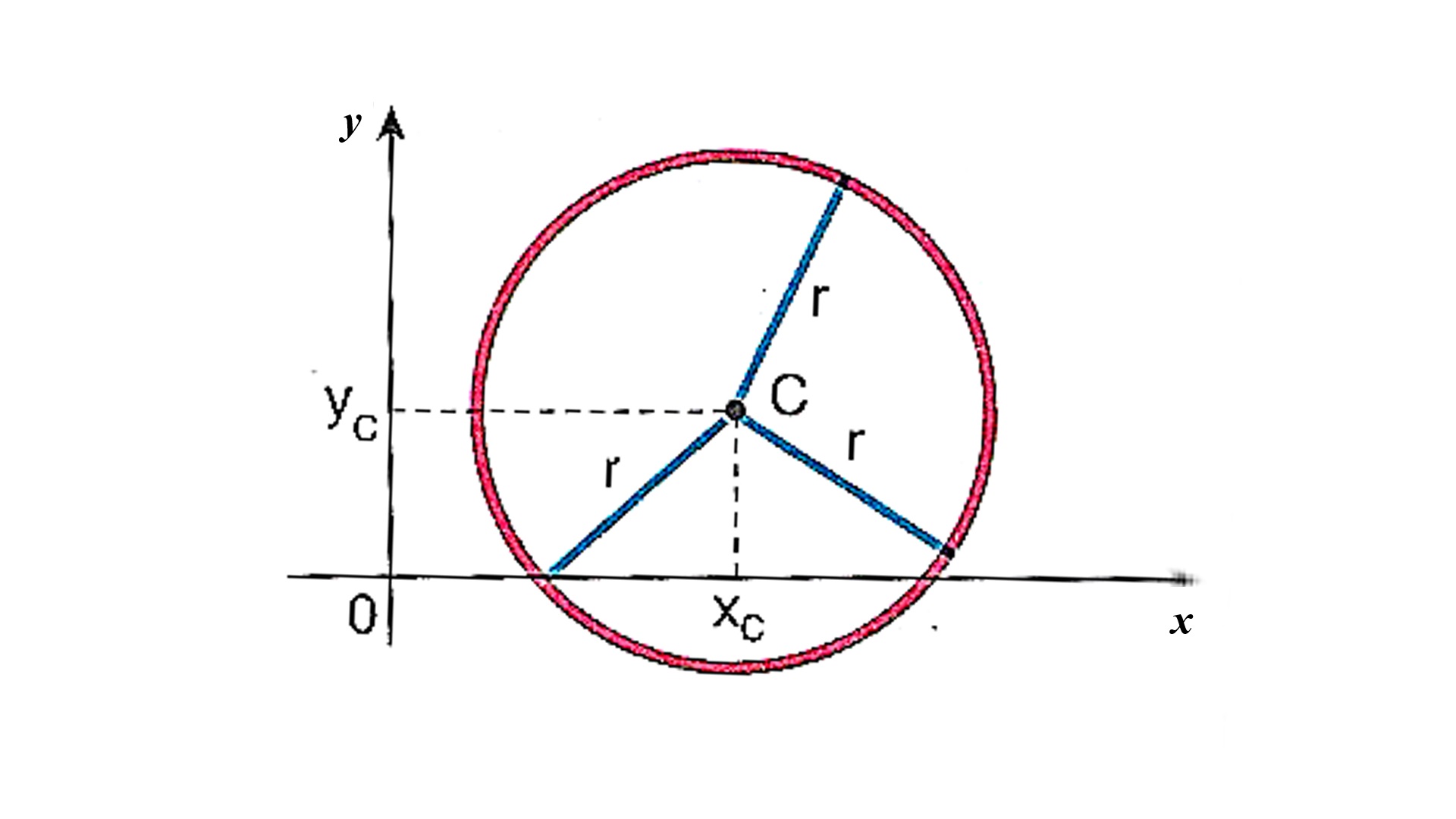
EXEMPLO: \left(x-1 \right)^2+ \left(y+4 \right)^2 = 9 é a equação reduzida da circunferência de centro C(1,-4) e raio r = 3 . Notemos, por exemplo, que ponto (4,-4) pertence à circunferência, pois \left(4-1 \right)^2+ \left(-4 + 4 \right)^2 = 9 , mas a origem do sistema de coordenadas não pertence à circunferência, pois \left(0-1 \right)^2+ \left(0+4 \right)^2 \neq 9 .
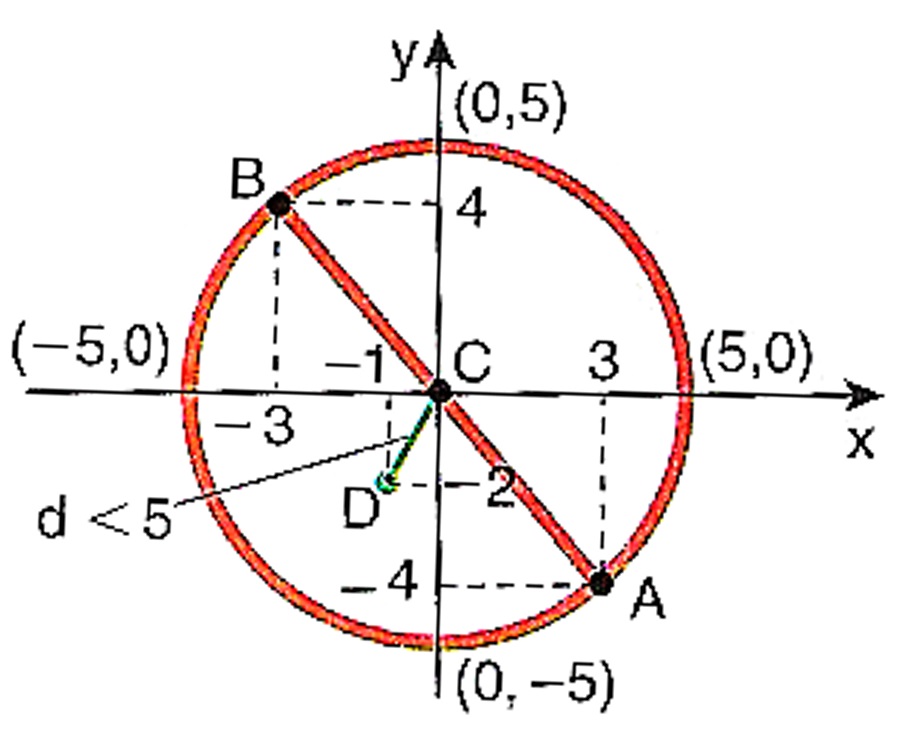
EXEMPLO: A equação $$x^2 + y^2 = 25 $$ é de uma circunferência de centro na origem e raio 5 , e o ponto A(3,-4) pertence a ela, pois 3^3 + (-4)^2 = 25 ; já o ponto D(-1,-2) não pertence à circunferência, pois (-1)^2 + (-2)^2 \neq 25, ou seja, as coordenadas do ponto não verificam a equação da circunferência. Notemos que tomando B(-3,4) , o segmento \overline{AB} é um diâmetro, cujo ponto médio é, evidentemente, o ponto C , centro da circunferência.
A Equação Geral da Circunferência
Retomemos a forma reduzida da equação de uma circunferência $$ \left(x-x_C \right)^2+ \left(y-y_C \right)^2 = r^2, $$ e desenvolvamos os quadrados. Agrupando os termos convenientemente, temos: $$ x^2 -2x x_C + x_C^2+y^2-2y y_C + y_C^2 = r^2$$ e, assim, $$ x^2 + y^2 -2x x_C -2y y_C + \left( x_C^2 + y_C^2 – r^2 \right) = 0 .$$ Esta expressão é conhecida como forma geral da equação da circunferência, ou equação geral da circunferência com centro C \left( x_C , y_C \right) e raio r .
Podemos escrever esta equação na forma $$Ax^2 + By^2 +Cxy +Dx +Ey+F = 0.$$ Porém, nem toda equação nesta forma, com coeficientes reais representa uma circunferência. Para que esta equação represente uma circunferência se
1. A = B \neq 0 ;
2. C = 0 ;
3. x_C = \frac{-D}{2A} ;
4. y_C = \frac{-E}{2A} ;
5. r = \sqrt{ \frac{D^2 + E^2 - 4AF}{4A^2} }, com D^2 + E^2 - 4AF > 0 .
EXEMPLO: Para averiguar se a equação x^2 + y^2 - 8x + 4y + 11 = 0 representa alguma circunferência (e, em caso afirmativo, qual circunferência), devemos estudar as condições:
1. A = B = 1 \neq 0 ;
2. C = 0 , afinal não há termo em x(x,y) ;
3. x_C = \dfrac{-D}{2A} = \dfrac{-(-8)}{2 \times 1} = 4 ;
4. y_C = \dfrac{-E}{2A} = \dfrac{-4}{2 \times 1} = -2;
5. r = \sqrt{ \frac{D^2 + E^2 - 4AF}{4A^2} } = \sqrt{ \frac{(-8)^2 + (4)^2 - 4\times 1 \times 11}{4\times 1^2} } = \sqrt{\dfrac{36}{4} } = 3 .
Portanto, a equação x^2 + y^2 - 8x + 4y + 11 = 0 representa a circunferência de centro (4, -2) e raio 3 .
Na forma reduzida, escreveríamos: $$ (x-4)^2 + (y+2)^2 = 9.$$
EXEMPLO: Verifique se a equação 2x^2 + 2y^2 +4x -12y +22 = 0 representa alguma circunferência. É necessário estudar as condições:
1. A = B = 2 \neq 0 ;
2. C = 0 ;
3. x_C = \dfrac{-4}{2 \times 2} = -1 ;
4. y_C = \dfrac{-(-12)}{2 \times 2} = 3 ;
5. D^2 + E^2 - 4AF = 4^2 + (-12)^2-4 \times 2 \times 22 = 16 + 144 -176 = -16 < 0 .
Como não se verifica a 5ª condição, não se trata de equação de circunferência.
Posições Relativas Entre o Ponto e Circunferência
Vimos que todos os pontos de uma circunferência distam igualmentemde centro e, mais, mantêm distência igula ao raio. Ora, dada uma circunferência de centro C e raio r , se outro ponto não distar de C exatamente o raio r , ele não pertencerá à circunferência, ou seja, será interno ou externo a ela.
Para uma circunferência de centro C\left( x_C , y_C \right) e raio r e um ponto P qualquer, compararemos d_{PC} com r .
Há três caos possíveis:
1. Se d_{PC} = r, então P pertence à circunferência;
2. Se d_{PC} > r , então P é externo à circunferência;
3. Se d_{PC} < r , então P é interno à circunferência;
Abaixo temos as ilustrações correspondentes:

Alternativamente, para pouparmos cálculos no caso de ser dada a equação geral da circunferência, podemos simplesmente substituir as variáveis x e y da equação pelas coordenadas do ponto P em questão.
Resumindo, dados um ponto P(x,y) e a equação geral $$Ax^2 + By +Cxy +Dx + Ey + F = 0,$$ com todas as condições para que ela represente uma circunferência satisfeitas, basta substituirmos na equação as coordenadas do ponto dado e obtermos o valor M da expressão do 1º membro da equação.
1. Se M = 0 , então P é o ponto da circunferência;
2. Se M < 0 , então P é um ponto interno da circunferência;
3. Se M > 0 , então P é um ponto externo da circunferência.
EXEMPLO: Tomemos a circunferência de centro C(3,4) e raio 5 .

Sua equação reduzida é $$ (x-3)^2 + (y-4)^2 = 25.$$ Vejamos que a circunferência passa pela origem do sistem, pois $$ (0-3)^2 + (0-4)^2 = 25.$$ O mesmo ocorre com o ponto P(8,4) . Já os pontos Q(-2,0) e R(2,1) não pertencem à circunferência, pois:
- para Q : (-2-3)^2+(0-4)^2 = (-5)^2 + (-4)^2 = 41 > 25 ;
- para R : (2-3)^2+(1-4)^2 = (-1)^2 + (-3)^2 = 10 < 25 .
Notemos que $$ d_{QC} = \sqrt{(-2-3)^2 + (0-4)^2} = \sqrt{(-5)^2 + (-4)^2} = \sqrt{41 } >5 = r$$ e $$ d_{RC} = \sqrt{(2-3)^2+(1-4)^2} = \sqrt{(-1)^2 + (-3)^2} = \sqrt{10} < 5 = r .$$ Trata-se, portanto, de uma simples comparação de distâncias.
EXEMPLO: Para a circunferência de equação $$x^2 + y^2 – 6x – 2y +6 = 0$$ e o ponto P(2,1), podemos fazer $$2^2 + 1^2 – 6 \times 2 – 2 \times 1 +6 = -3 <0 $$ e concluir que o ponto P é interno à circunferência.
Já o ponto Q(5,1) pertence à circunferência, pois $$5^2 + 1^2 – 6 \times 5 – 2 \times 1 + 6 = 0$$ e o ponto R(6,2) é externo a ela, pois: $$ 6^2 + 2^2 – 6 \times 6 -2 \times 2 + 6 = 6 > 0 .$$
Posições Relativas Entre Reta e Circunferência
Seja uma circunferência \lambda de centro C \left( x_C , y_C \right) e raio r . Existem, no plano, retas que cortam a circunferência em dois pontos, retas que tocam a circunferência em apenas um ponto e outras que não interceptam a circunferência em ponto algum.
Essas retas são chamadas, respectivamente: secantes, tangentes e externas à circunferência. Na figura abaixo
- u \cap \lambda = \emptyset e a reta u é externa à circunferência;
- t \cap \lambda = \{ T \} e a reta t é tangente à circunferência;
- s \cap \lambda = \{ S_1 , S_2 \} e a reta s é secante à circunferência;

EXEMPLO: Examinaremos a posição relativa entre a reta r: 2x+y-2 = 0 e a circunferência \lambda: (x-1)^2 + (y-5)^2 = 5 , procurando as eventuais interseções entre as duas. Isolando y na equação da reta e substituindo na da circunferência, teremos: $$y = 2-2x \text{ e } x^2 +(2 – 2x)^2 – 2x – 10 (2-2x) +21 = 0 \Rightarrow $$ $$ \Rightarrow x^2 + 2x +1 = 0 .$$
Como o discriminante \Delta dessa equação é nulo, há somente uma raíz real, que é x = -1 . Substituindo de volta na equação da reta, obtemos y = 2 -2 \times (-1) , ou seja, y = 4 . Assim, a interseção entre a reta e a circunferência é única e é o ponto P(-1,4) . Dessa forma, a reta e a circunferência são tangentes.
EXEMPLO: Façamos o mesmo que no exemplo anterior, agora entre a reta 3x - y = 0 e a circunferência x^2 + y^2 - 6x - 8y = 0. Isolando y na equação da reta e substituindo na equação da circunferência, temos $$ y = 3x \text{ e } 10x^2 – 30x = 0,$$ equação que tem 900 como valor do discriminante, motivo pelo qual há duas raízes reais distintas, que são x = 0 e x = 3 .
Substituindo esses valores de volta na equação da reta, obtemos os pontos P_1 (0,0) e P_2 (3,9) ; como a reta e a circunferência têm dois pontos de interseção, dizemos que a reta e a circunferência são secantes.
EXEMPLO: Para determinarmos a posição relativa entre a reta $$x-y-1=0$$ e a circunferência $$ x^2 +y^2 +2x-2y+1=0,$$ procederemos da mesma maneira: $$ y = x-1 \Rightarrow x^2 + (x-1)^2 + 2x -2(x-1) +1 = 0 \Rightarrow \\ \Rightarrow x^2-x+2 = 0 .$$ Essa última equação possui discriminante negativo ( \Delta = -7 ) e, portanto, não possui raízes reais. Assim, não há pontos de interseção entre a reta e a circunferência, ou seja, a reta é exterma à circunferência.
Posições Relativas entre duas Circunferências
Sejam as circunferências coplanares L_1 , de centro C_1 \left( x_1 , y_1 \right) e raio r_1 , e L_2 , de centro C_2 \left( x_2 , y_2 \right) e de raio r_2 .
L_1 e L_2 podem:
1. ter dois pontos comuns; logo, L_1 e L_2 são secantes entre si. 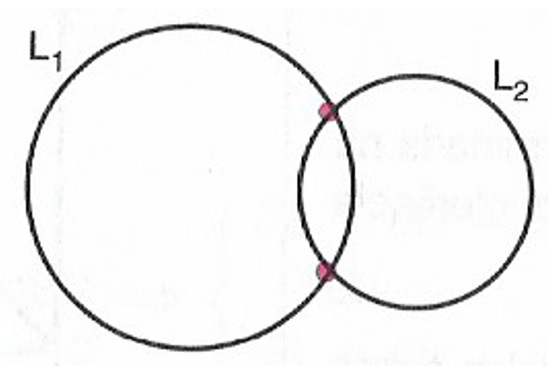
2. ter um ponto em comum; logo, L_1 e L_2 são tangentes entre si.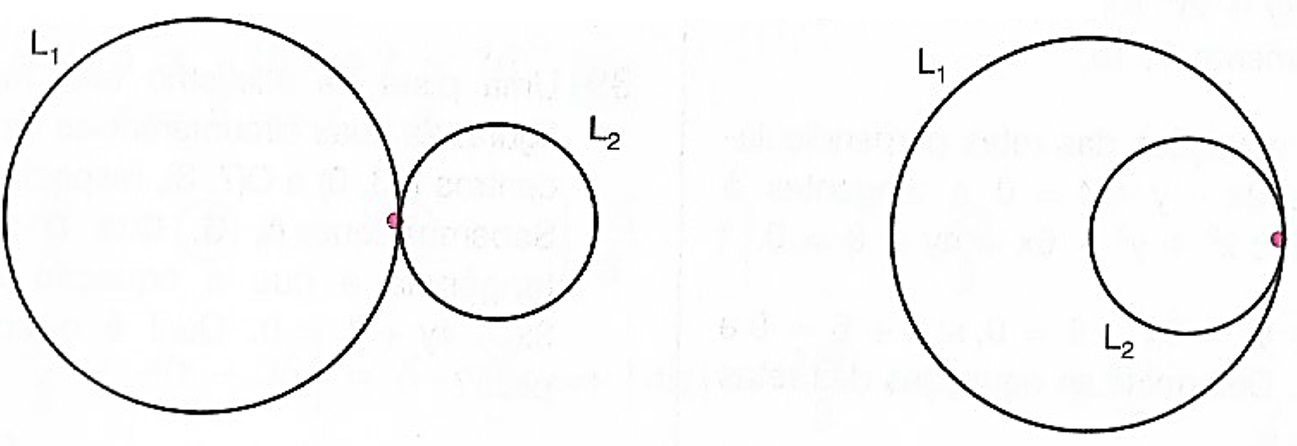
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
3. não ter ponto em comum; logo, L_1 e L_2 são disjuntas. 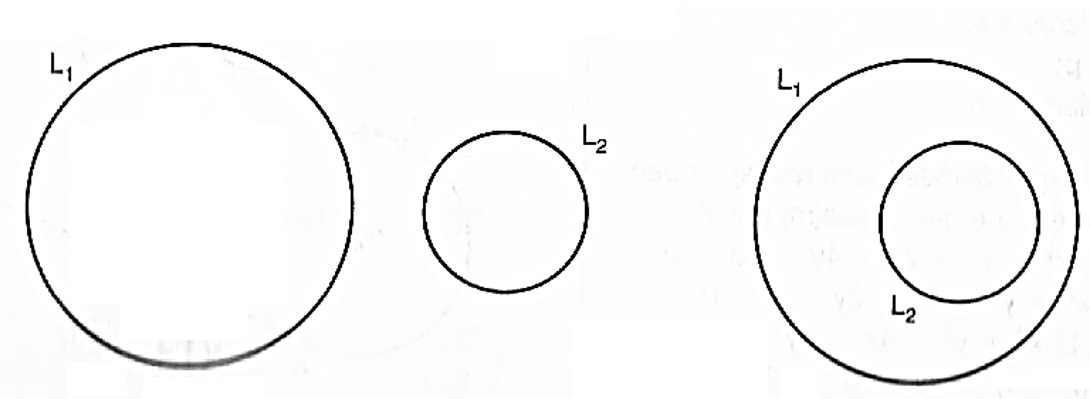
Analisando o sistema S formado pelas equações de L_1 e de L_2 : $$ (x-a_1)^2 + (y-b_1)^2 = r_1^2 \\ (x-a_2)^2 + (y-b_2)^2 = r_2^2 $$ temos que
1. L_1 e L_2 são secantes entre si se S tem duas soluções;
2. L_1 e L_2 são tangentes entre si se S tem uma única solução.
3. L_1 e L_2 são disjuntas se S não tem solução.
Podemos, também, analisar a posição relativa entre L_1 e L_2 comparando a distância d entre os centros C_1 e C_2 como r_1 + r_2 e com | r_1 + r_2 | :

1) Se d = 0 então L_1 e L_2 são concêntricas (como na figura 1);
2) Se d = |r_1 - r_2 | ou d = r_1 + r_2 , então L_1 e L_2 são tangentes (figuras 2 e 3, respectivamente). Note que, se L_1 e L_2 são tangentes entre si, o ponto de tangência e os centros C_1 e C_2 são colineares.
Comparando a figura 4 com as figuras 1 e 2, vem:
3) se 0 < d <| r_1 - r_2 | ou se d > r_1 + r_2 , então L_1 e L_2 são disjuntas (figura 6).
Comparando a figura 5 com as figuras 2 e 3, vem:
4) se | r_1 - r_2 | < d < r_2 + r_2 , então L_1 e L_2 são secantes.
EXEMPLO: Sejam L_1 de centro C_1 (2,1) e raio r_1 = 2 , L_2 de centro C_2 (8,4) e raio r_2 = 2 + 3 \sqrt{5} e L_3 de centro C_3 (6,3) e raio r_3 = 3 . Temos:
1) Posição entre L_1 e L_2 :
$$ | r_1 – r_2 | = 3 \sqrt{5}, \qquad r_1 + r_2 = 4 + 3 \sqrt{5} $$ $$ d_{C_1 C_2} = \sqrt{(2-8)^2 + (1-4)^2} = \sqrt{45} = 3 \sqrt{5}.$$ Logo, como | r_1 - r_2 | = d_{C_1 C_2} , então L_1 e L_2 são tangentes.
2) Posição entre L_1 e L_3 :
$$ | r_1 – r_3 | = 1, \qquad r_1 + r_3 = 5 $$ $$ d_{C_1 C_3} = \sqrt{(2-6)^2 + (1-3)^2} = \sqrt{20} = 2 \sqrt{5}.$$ Logo, como | r_1 - r_3 | < d_{C_1 C_3} < r_1 + r_3 , então L_1 e L_3 são secantes.
3) Posição entre L_2 e L_3 :
$$ | r_2 – r_3 | = 3 \sqrt{5} -1, \qquad r_2 + r_3 = 5 + 3 \sqrt{5} $$ $$ d_{C_2 C_3} = \sqrt{(8-6)^2 + (4-3)^2} = \sqrt{5}.$$ Logo, como 0 < d_{C_1 C_3} < | r_2 - r_3 | , então L_2 e L_3 são disjuntas.
Assista nossa vídeo-aula completa sobre Circunferência
Os 5 Melhores Livros Sobre Geometria Analítica
- “Geometria Analítica: Um Tratamento Vetorial”, de Paulo Boulos e Ivan De Camargo.
- “Geometria Analítica”, de Alfredo Steimbruch e Paulo Winterle
- “Fundamentos de matemática elementar – Volume 7: Geometria analítica”, de Gelson Iezzi.
- “Coordenadas No Plano”, de Elon Lages Lima.
- “Coordenadas no Espaço”, de Elon Lages Lima.
