PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Na Geometria Analítica, o sistema de coordenadas polares é um sistema de coordenadas bidimensional no qual os pontos do plano cartesiano são dados por um ângulo e uma distância de um ponto central conhecido como origem (ou polo).
As coordenadas polares e outras mudanças de variáveis são úteis diversos casos onde são convenientes para o cálculo das integrais duplas, que definimos neste artigo. Nesse sentido, as equações $$x=r\cos{\theta}\;\;\;\;y=r\sin{\theta}$$ que nos dão as coordenadas cartesianas de um dado ponto em termos de suas coordenadas polares.
As coordenadas polares são uma foram de estabelecer um sistema de coordenadas no plano usando um ponto de referência chamado de polo, que no plano cartesiano está no mesmo ponto que usamos como a origem, ou seja, a interseção dos eixos coordenados.
Neste tipo de sistema de coordenas cada ponto no plano é determinado por uma distância à este ponto de referência e um ângulo, como dado pela figura abaixo.
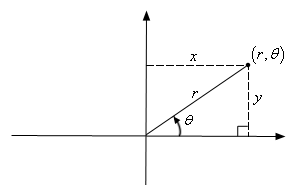
Neste sistema, ao invés de representar os pontos como (x,y) , podemos expressar este ponto com as coordenadas polares (r , \theta) , onde r \geq 0 e 0 \leq \theta \leq 2 \pi .
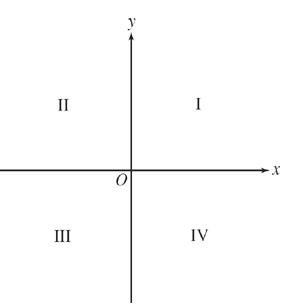
Os pontos de cada quadrante no plano podem ser diferenciados pelo ângulo, da seguinte maneira:
| Quadrante | Coordenadas Cartesianas | Amplitude Ângular |
|
| I | (x,y) | 0 < \theta < \dfrac{ \pi}{2} | |
| II | (-x,y) | \dfrac{ \pi}{2} < \theta < \pi | |
| III | (-x,-y) | \pi < \theta < \dfrac{ 3 \pi}{2} | |
| IV | (x,-y) | \dfrac{3 \pi}{2} < \theta < 2 \pi |
Fórmula de Coordenadas Polares
É possível escrever infinitos pontos usando coordenadas polares através de um único ponto, usando a fórmula $$ \left( r , \theta + 2 \pi n \right), \qquad n \in \mathbb{Z}$$
Os valores de \theta variam positivamente no sentido anti-horário e negativamente no sentido horário.
Relação entre Coordenadas Cartesianas e Coordenadas Polares
As equações $$x=r\cos{\theta}\;\;\;\;y=r\sin{\theta}$$ que nos dão as coordenadas cartesianas de um dado ponto em termos de suas coordenadas polares.
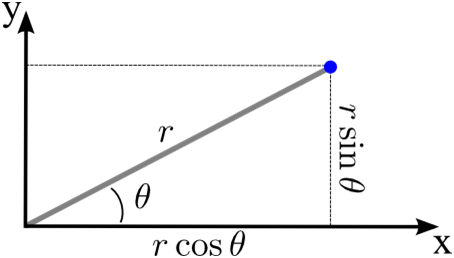
Observe que, nestas coordenadas $$ x^2 + y^2 = r^2 \text{cos}^2 ( \theta ) + r^2 \text{sen}^2 ( \theta ) = \\ r^2 \left[ \text{cos}^2 ( \theta ) + \text{sen}^2 ( \theta ) \right] = r^2 \\ r = \sqrt{ x^2 + y^2 }.$$ Além disso, $$ \frac{y}{x} = \frac{r \text{sen} ( \theta )}{r \text{cos} ( \theta )} \\ \frac{y}{x} = \text{tan} ( \theta ) \\ \theta = \text{arc tan} \left( \frac{y}{x} \right).$$
EXEMPLO: Converta as coordenadas polares do ponto \left( 4, \dfrac{\pi}{2} \right) em coordenadas cartesianas.
Solução: Dado o ponto \left( 4, \frac{\pi}{2} \right) , temos que $$ x = 4 \text{cos} \left( \frac{\pi}{2} \right) = 4 \times 0 = 0.$$ $$ y = 4 \text{sen} \left( \frac{\pi}{2} \right) = 4 \times 1 = 4.$$ Portanto, as coordenadas retangulares deste ponto no plano é (0,4) .
EXEMPLO: Converta as coordenadas retangulares do ponto (2,2) em coordenadas polares.
Solução: Dado o ponto (x,y) = (2,2) , temos que $$r = \sqrt{x^2 + y^2} = \sqrt{2^2 + 2^2} = 2 \sqrt{2} $$ e $$ \theta = \text{arctan}\left( \frac{y}{x} \right) = \text{arctan}\left( \frac{2}{2} \right) = \text{arctan}\left( 1 \right) = \frac{ \pi }{4}.$$ Portanto, as coordenadas polares deste ponto é \left( 2 \sqrt{2}, \dfrac{\pi}{4} \right) .
EXEMPLO: Uma circunferência com centro na origem e raio 1 tem equação dada por $$ x^2 + y^2 = 1.$$ Logo, os pontos desta circunferência são dados por $$ \left( \text{cos} ( \theta ), \text{sen} ( \theta ) \right), \qquad 0 \leq \theta < 2 \pi .$$
EXEMPLO: As coordenadas polares funcionam melhor na hora de escrever analiticamente regiões planas circulares. Por exemplo, o semi-círculo de centro na origem e raio 1 pode ser representado graficamente por
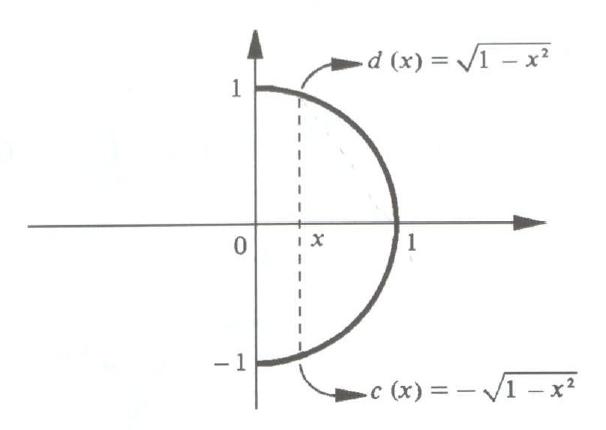
Para escrever esta região no plano em termos das coordenadas cartesianas, temos que
$$R: \left\{ \begin{array}{l}
0 \leq x \leq 1\\
-\sqrt{x^2+y^2}\leq y \leq \sqrt{x^2 + y^2}
\end{array} \right.$$
Fazendo x=r\cos{\theta} e r\sin{\theta}, escrevos esta região como $$R: \left\{ \begin{array}{l}
0 \leq r \leq 1\\
-\pi/2\leq \theta \leq \pi/2
\end{array} \right.$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
EXEMPLO: A região do plano delimitada por $$x^2+y^2 = 4\;\;\;\;e\;\;\;x^2+y^2=9$$ é o anel representado por
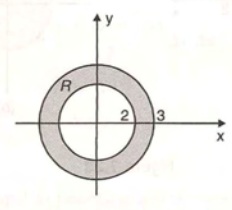que pode ser escrito em coordenadas polares como 2\leq r \leq 3 e 0\leq \theta \leq 2 \pi.
EXEMPLO: A região delimitada abaixo
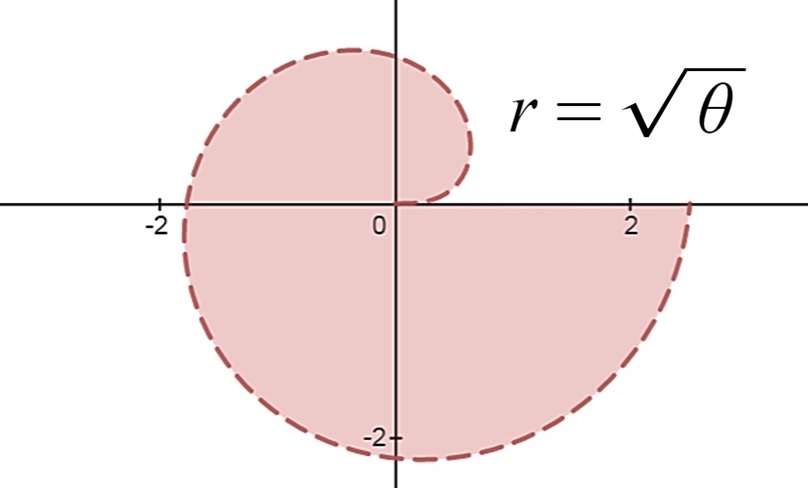
pode ser escrita analiticamente usando as coordenadas polares como $$ 0 \leq r \leq \sqrt{ \theta } \\ 0 \leq \theta \leq 2 \pi .$$
EXEMPLO: Usando coordenadas polares podemos escrever uma elipse. Considere a elipse dada por $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$ Inspirados pela relação $$\cos^2{t}+\sin^2{t}=1$$ temos que
\begin{eqnarray}
x & = & a\cos{t}\\
y & = & b\sin{t} \;\;\;\;\;\;\;\;\;\;\;\;\;t\in[0,2\pi]
\end{eqnarray}
Ou seja, todos os pontos da elipse serão dados por $$\left( a\cos{t} , b\sin{t} \right), \qquad \theta in [0, 2 \pi ].$$