Como Calcular Volumes e Áreas com Integrais Múltiplas?

Podemos usar as Integrais Duplas e Triplas para calcular volumes de sólidos no espaço tridimensional e, também, de áreas planas no espaço bidimensional ou de áreas de superfícies no espaço tridimensional

Nesse artigo queremos estabelecer formas de calcular volumes e áreas de superfícies geradas pelo gráficos dessas funções através da Integração Múltiplas.

Consequentemente, neste artigo, estaríamos trabalhando com as interpretações geométricas das integrais dupla e tripla nos espaços vetoriais de dimensões adequadas.

Interpretação Geométrica da Integral Dupla: Cálculo de Volume

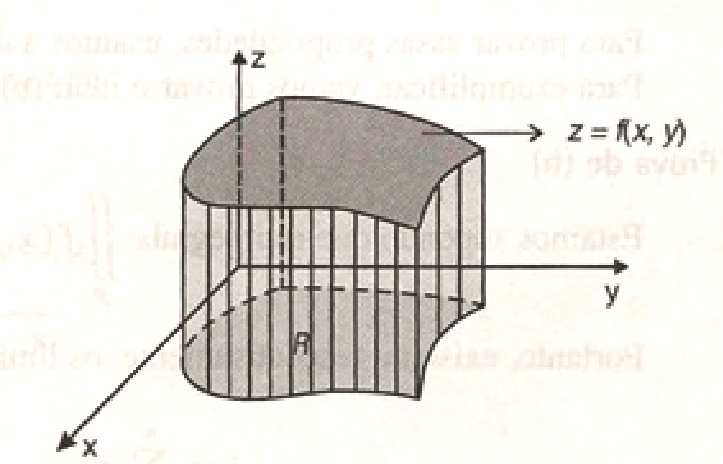
Suponhamos que z=f(x,y) seja maior ou igual a zero sobre R. Assim, a $$\int \int_{R}{f(x,y)}dxdy \geq \int \int_{R}{g(x,y)}dxdy$$ nos dá o volume do sólido delimitado superiormente pelo gráfico de z=f(x,y) , inferiormente pela região R e lateralmente pelo “cilindro” vertical cuja base é o contorne de R.

EXEMPLO

Calcular o volume do sólido delimitado superiormente pelo gráfico de z=4-x-y, inferiormente pela região R delimitada por x=0, x=2, y=0 e y=\frac{1}{4}x + \frac{1}{2} e lateralmente pela base do cilindro vertical cuja base é o contorno de R.

\begin{eqnarray*}
\int_{0}^{2} \left[ \int_{0}^{\frac{1}{4}x+\frac{1}{2}}{(4-x-y)dy} \right]dx & = & \int_{0}^{2} \left[ 4y-xy-\frac{y^2}{2} \right]_{0}^{\frac{1}{4}x+\frac{1}{2}} dx\\
& = & \int_{0}^{2} \left[-\frac{9}{32}x^2 + \frac{3}{8}x +\frac{15}{8} \right]dx\\
& = & \left[-\frac{3}{32}x^3 + \frac{3}{16}x^2 +\frac{15}{8}x \right]_{0}^{2}\\
& = & \frac{15}{4}
\end{eqnarray*}

EXEMPLO

Calcular o volume do sólido abaixo do plano xy delimitado por z=x^2+y^2 -9.

Observe que para z=x^2+y^2 -9 \leq 0 para x^2+y^2 \leq 9 que é a região de integração R. Sendo assim, devemos calcular o módulo da integral dupla que calcula o volume desejado. Ou seja,

$$V = \left| \int \int_{R}{(x^2 +y^2-9)dxdy} \right|.$$ Utilizando coordenadas polares temos que 0 \leq \theta \leq 2\pi e 0 \leq r \leq 3. Desta forma,
\begin{eqnarray*}
V & = & \left| \int \int_{R}{(x^2 +y^2-9)dxdy} \right|\\
& = & \left| \int\limits_{0}^{2\pi} \int \limits_{0}^{3}{(r^2-9)rdrd\theta} \right|\\
& = & \left| \int\limits_{0}^{2\pi} {\left[ \frac{r^4}{4} – \frac{9}{2}r^2 \right]_{0}^{3}d\theta} \right|\\
& = & \left| \int\limits_{0}^{2\pi} {\left[ – \frac{81}{4} \right] d\theta} \right|\\
& = & \frac{81}{2}\pi
\end{eqnarray*}

Área de Figuras Planas

A área A de uma superfície \mathbb{S} é definida pela integral dupla $$A = \int \int_{R}{dA},$$ onde

1. dA = \left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\| dudv, se \mathbb{S} é denotada em sua forma paramétrica r(u,v);
2.  dA = \sqrt{1+\left( \frac{\partial g}{\partial x}\right)^2 + \left( \frac{\partial g}{\partial y}\right)^2}dxdy se \mathbb{S} é denotada em sua forma explícita z=g(x,y)

EXEMPLO

Calcule a área da superfície esférica com centro na origem e raio a>0.

Sabemos que $$A = \int \int_{R}{dA},$$ onde R é o círculo com centro na origem e raio igual a a.

Observe que a superfície da esfera acima do plano xOy pode ser escrita como $$g(x,y) = \sqrt{a^2 -x^2 – y^2},$$  e a área total da esfera é o dobro do valor dessa área.

Logo, $$A = \int \int_{R}{dA} = 2 \int \int_{R}{\sqrt{1+\left( \frac{\partial g}{\partial x}\right)^2 + \left( \frac{\partial g}{\partial y}\right)^2}dxdy}$$ onde R é o círculo com centro na origem e raio a.

Ou seja, $$A = \int \int_{R}{\sqrt{1+ \frac{x^2 + y^2}{a^2 – x^2 – y^2}}dxdy} = \int_{0}^{2 \pi} \int_{0}^{a}{\sqrt{\frac{a^2}{a^2 – r^2}}r dr d \theta}=$$ $$= 2 \pi \int_{0}^{a}{\sqrt{\frac{a^2}{a^2 – r^2}}r dr = 4 \pi a^2 .$$

Calculando Volume com Integrais Triplas

Agora queremos estabelecer formas de calcular volumes de sólidos utilizando a Integral Tripla.

Isto seria uma interpretação geométrica da integral tripla na terceira dimensão.

Seja T um subconjunto do \mathbb{R}^3, limitado fechado. Definimos o volume de T por $$V_{T} = \int \int\limits_{T} \int{dxdydz}$$

EXEMPLO

Calcule o volume de todos os pontos do espaço tais que x^2+y^2\leq z \leq 2-x^2 -y^2.

Note que os pontos de interseção das duas superfícies é dado por $$x^2+y^2=2-x^2-y^2 \Leftrightarrow x^2+y^2=1,$$ ou seja, estão numa circunferência de raio 1.

Reduzindo a integral tripla para uma integral dupla e usando as coordenadas polares obtemos:

\begin{eqnarray*}
V & = & \int\limits_{-1}^{1} \int\limits_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}\int\limits_{x^2+y^2}^{2-x^2 -y^2}dzdy dx\\
& = & 2 \int\limits_{-1}^{1} \int\limits_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}{(1-x^2-y^2)}dyddx \\
& = & 2 \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi}{(1-r^2)}r drd\theta\\
& = & 4\pi \int\limits_{0}^{1}{(r-r^3)} drd\theta\\
& = & 4\pi \left[ \dfrac{r^2}{2}- \dfrac{r^4}{4} \right] _{0}^{1} \\
& = & \pi
\end{eqnarray*}

Exercícios Resolvidos: Cálculo de Volume e Área Usando Integrais Múltiplas:

• Volume com Integrais Triplas | 1ª Lista de Exercícios Resolvidos
• Mudança de Variável em Integrais Triplas | 1ª Lista de Exercícios Resolvidos
• Integrais Triplas | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• As Integrais Triplas
• Mudança de Variável em Integrais Triplas | Coordenadas Cilíndricas e Esféricas
• Mudança de Variável em Integrais Duplas | Coordenadas Polares
• Integrais Duplas | Funções de Várias Variáveis

Assista Nossa Vídeo-Aula