Coordenadas Polares e a Mudança de Variável nas Integrais Duplas

As coordenadas polares e outras mudanças de variáveis são úteis diversos casos onde são  convenientes para o cálculo das integrais duplas, que definimos neste artigo.

Na integração de funções de uma variável, a fórmula da substituição ou da mudança de variáveis é utilizada para transformar a integral dada em outra mais simples. Temos, para uma função f(x), que $$\int_{a}^{b}{f(x)} = \int_{c}^{d}{f(g(t))g'(t)dt}, $$ onde a = g(c) e b=g(d).

Para integrais duplas, podemos utilizar um procedimento análogo, por meio das mudanças de variáveis $$x = x(u,v)\;\;\;e\;\;\;y=y(u,v),$$ uma integral dupla sobre uma região R do plano xy pode ser transformada em uma integral dupla sobre uma região R' do plano uv.

Nesse artigo queremos estabelecer o conceito de Mudança de Variável para Integral Dupla para esse tipo de função com domínio no \mathbb{R} ^2.

Mudança de Variável em Integrais Duplas

Na integração de funções de uma variável, a fórmula da substituição ou da mudança de variáveis é utilizada para transformar a integral dada em outra mais simples. Temos, para uma função f(x), que $$\int_{a}^{b}{f(x)} = \int_{c}^{d}{f(g(t))g'(t)dt}, $$ onde a = g(c) e b=g(d). Para integrais duplas, podemos utilizar um procedimento análogo, por meio das mudanças de variáveis $$x = x(u,v)\;\;\;e\;\;\;y=y(u,v),$$ uma integral dupla sobre uma região R do plano xy pode ser transformada em uma integral dupla sobre uma região R' do plano uv.

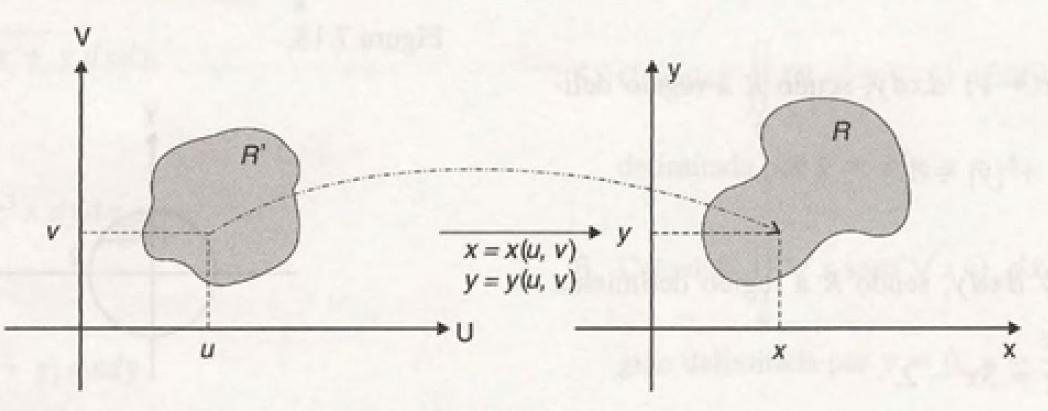
Desta forma, temos que

$$\int \int_{R}{f(x,y)}dxdy = \int \int_{R’}{f(x(u,v),y(u,v)}\left| \frac{\partial (x,y)}{\partial (u,v)} \right| dudv$$ onde \left| \frac{\partial (x,y)}{\partial (u,v)} \right| é o determinante jacobiano de x e y em relação a u e v, dado por $$\left| \frac{\partial (x,y)}{\partial (u,v)} \right| = \left| \begin{array}{ll}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\
\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}
\end{array}
\right|$$

EXEMPLO

Calcule $$\int \int_{R}{\frac{\cos{(x-y)}}{\sin{x+y}}}dxdy$$ sendo R o trapézio $$1\leq x+y \leq 2,\;\;\;x\geq o,\;\;\;y\geq 0.$$

Considere u=x-y e v=x+y. Desta forma, $$x=\frac{u}{2}+\frac{v}{2}\;\;\;e\;\;\;y=\frac{u}{2}-\frac{v}{2},$$ assim
$$\left| \frac{\partial (x,y)}{\partial (u,v)} \right| = \left| \begin{array}{ll}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\
\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}
\end{array}
\right| = \left| \begin{array}{ll}
\frac{1}{2} & \frac{1}{2}\\
\\
-\frac{1}{2} & \frac{1}{2}
\end{array}
\right| = \frac{1}{2}$$

Portanto, queremos calcular $$\int \int_{R}{\frac{\cos{u}}{\sin{v}}}dxdy$$ sendo R o trapézio $$1\leq v \leq 2,\;\;\;-v \leq u \leq v,$$ ou seja,

$$\int_{1}^{2} \int_{-v}^{v}{\frac{\cos{u}}{\sin{v}}}dudv=1$$

Coordenadas Polares

As equações $$x=r\cos{\theta}\;\;\;\;y=r\sin{\theta}$$ que nos dão as coordenadas cartesianas de um dado ponto em termos de suas coordenadas polares.

O determinante jacobiano, nesse caso, é dado por $$\left| \frac{\partial (x,y)}{\partial (u,v)} \right| = \left| \begin{array}{ll}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\
\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}
\end{array}
\right| = \left| \begin{array}{ll}
\cos{\theta} & -r\sin{\theta}\\
\\
\sin{\theta} & r\cos{ \theta}
\end{array}
\right| = r$$ e, desta forma, $$\int \int_{R}{f(x,y)}dxdy = \int \int_{R’}{f(r\cos{\theta}, r\sin{\theta})r}drd\theta$$

EXEMPLO

Calcule $$\int \int_{R}{(x-y)}dxdy$$ sendo R o semi-círculo de centro na origem e raio 1.

Temos que
$$R: \left\{ \begin{array}{l}
0 \leq x \leq 1\\
-\sqrt{x^2+y^2}\leq y \leq \sqrt{x^2 + y^2}
\end{array} \right.$$

Fazendo x=r\cos{\theta} e r\sin{\theta}, encontramos

$$\int \int_{R’}{(r(\cos{\theta}-\sin{\theta})}rdrd\theta = \int \int_{R’}{(r^2(\cos{\theta}-\sin{\theta})}drd\theta = \frac{2}{3}$$ com

$$R’: \left\{ \begin{array}{l}
0 \leq r \leq 1\\
-\pi/2\leq \theta \leq \pi/2
\end{array} \right.$$

EXEMPLO

Calcular $$\int \int_{R}{\sqrt{x^2+y^2}}dxdy$$ sendo R o círculo de centro na origem e raio 2.

Nossa região R se reduz à região R' dada por

$$R: \left\{ \begin{array}{l}
0 \leq r \leq 2\\
0 \leq \theta \leq 2\pi
\end{array} \right.$$

que é dada pela figura

Portanto
$$\int \int_{R}{\sqrt{x^2+y^2}}dxdy = \int_{0}^{2\pi} \int_{0}^{2}{r^2}drd\theta = \frac{16 \pi}{3}. $$

EXEMPLO

Calcular $$I=\int \int_{R}{e^{x^2+y^2}dxdy}$$, onde R é a região do plano xy delimitada por $$x^2+y^2 = 4\;\;\;\;e\;\;\;x^2+y^2=9.$$

em coordenadas polares $$e^{x^2+y^2} = e^{r^2},$$ com 2\leq r \leq 3 e 0\leq \theta \leq 2 \pi. Ou seja,
\begin{eqnarray*}
I & = & \int \int_{R}{e^{x^2+y^2}dxdy}\\
& = & \int\limits_{0}^{2\pi} \int\limits_{2}^{3}{e^{r^2}r dr d\theta}\\
& = & \int\limits_{0}^{2\pi} {\left[ e^{r^2} \right]_{2}^{3}d\theta} \\
& = & \frac{1}{2}\int\limits_{0}^{2\pi}{\left(e^{9} – e^{4}\right) d\theta}\\
& = & \frac{1}{2} \left[\theta \left(e^{9} – e^{4}\right)\right]_{0}^{2\pi}\\
& = & \pi \left(e^{9} – e^{4}\right)
\end{eqnarray*}

Exercícios Resolvidos sobre Mudança de Variável nas Integrais Duplas:

• Mudança de Variável na Integral Dupla | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• Calculando Volume e Área de Superfície com Integrais Duplas
• Integrais Duplas | Funções de Várias Variáveis
• Máximos e Mínimos: O Método dos Multiplicadores de Lagrange
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais

Assista Nossa Vídeo-Aula Sobre o Tema: