Mudança de Variável em Integrais Triplas | 1ª Lista de Exercícios Resolvidos

Em alguns casos especiais no estudo da integral tripla é conveniente usar mudanças de variáveis como, por exemplo, as coordenadas cilíndricas e esféricas. Sabemos que as integrais triplas são o análogo de integrais duplas em três dimensões. Elas são uma ferramenta para somar infinitamente grandezas infinitesimais associadas a pontos em uma região tridimensional.

Introduzindo novas variáveis de integração u,v,w por meio de equações x=x(u,v,w), y=y(u,v,w) e z=z(u,v,w), a integral original pode ser expressa como
$$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T} \int{f(x(u,v,w), y(u,v,w), z(u,v,w))\left| \frac{\partial (x,y,z)}{\partial (u,v,w)} \right| dudvdw}$$ onde o determinante jacobiano de x,y e z em relação a u, v e w dado por $$\left| \frac{\partial (x,y,z)}{\partial (u,v,w)} \right| = \left| \begin{array}{ccc}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\
\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\
\\
\frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w}\\\end{array}
\right|$$

Em coordenadas cilíndricas, obtemos $$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T’} \int{f(r \cos{\theta}, r \sin{\theta}, z)r drd\theta dz}$$ onde T' é a região T descrita em coordenadas cilíndricas. Já em coordenadas esféricas, $$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T’} \int{f(r \cos{\theta}\sin{\phi}, r \sin{\theta}\sin{\phi}, r\cos{\phi})r^2\sin{\phi} drd\theta d\phi }$$ onde T' é a região T descrita em coordenadas esféricas.

Exercícios Resolvidos sobre Mudanças de Variáveis em Integrais Triplas

1) Calcule \int\limits_{T} \int \int{f(x,y,z)dxdydz} onde:

(a) f(x,y,z) = x^2 + y^2 e T é o cilindro x^2+y^2 \leq 1, 0 \leq z \leq 4

Nesse caso, o sólido T sera escrito em coordenadas cilíndricas. Com isso, suas variáveis estarão entre constantes: $$ 0 \leq r \leq 1$$ $$0 \leq \theta \leq 2 \pi$$ $$0 \leq z \leq 4.$$

Assim, $$\int\limits_{T} \int \int{f(x,y,z)dxdydz} = \int_{0}^{1} \int_{0}^{2 \pi} \int_{0}^{4}{r^3 dz dr d\theta}.$$ Como a função de integração não depende de \theta nem de z, então podemos multiplicar a integral pelas suas amplitudes, logo $$ \int_{0}^{1} \int_{0}^{2 \pi} \int_{0}^{4}{r^3 dz dr d\theta} = 8 \pi \int_{0}^{1}{r^3 dr} = 2  \pi$$

(b) f(x,y,z) = 1, onde T é a esfera x^2 + y^2 + z^2 = 4.

Nesse caso, o sólido T sera escrito em coordenadas esféricas. Com isso, suas variáveis estarão entre constantes: $$ 0 \leq r \leq 2$$ $$0 \leq \theta \leq 2 \pi$$ $$0 \leq \varphi \leq \pi.$$

Assim, $$\int\limits_{T} \int \int{f(x,y,z)dxdydz} = \int_{0}^{2} \int_{0}^{2 \pi} \int_{0}^{\pi}{r^2sen \varphi d\varphi d\theta dr}.$$

Como a função de integração não depende de \theta  então podemos multiplicar a integral pela sua amplitude, logo $$ \int_{0}^{2} \int_{0}^{2 \pi} \int_{0}^{\pi}{r^2sen \varphi d\varphi d\theta dr} = 2\pi \int_{0}^{2} \int_{0}^{\pi}{r^2 sen \varphi d\varphi  dr} = $$ $$= \frac{16}{3} \pi \int_{0}^{\pi}{sen \varphi d\varphi} = \frac{32}{3} \pi.$$

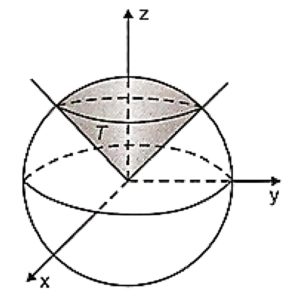
(c) f(x,y,z) = z e T é a  região do espaço limitada superiormente pela esfera x^2 + y^2 +z^2 = 16 e inferiormente pelo cone z = \sqrt{x^2+y^2}.

SOLUÇÃO: O sólido T pode ser visto na figura abaixo e em coordenadas esféricas ela será escrita como $$T: \left\{ \begin{array}{l} 0 \leq r \leq 4\\ 0 \leq \theta \leq \pi /2\\ 0 \leq \phi \leq \pi /4\end{array} \right.$$

Portanto, $$\int \int \int\limits_{T}{z dxdydz} = \int \int \int\limits_{T}{r cos(\phi) r^2 sen(\phi) dr d \theta d \phi} = $$ $$ = \int\limits_{0}^{2 \pi } \int \limits_{0}^{\pi /4} \int \limits_{0}^{4} {r^3 cos(\phi) sen(\phi) dr d \phi d \theta} = \int\limits_{0}^{2 \pi } \int \limits_{0}^{\pi /4}{64 cos(\phi) sen(\phi) d \phi d \theta}  = 32 \pi.$$

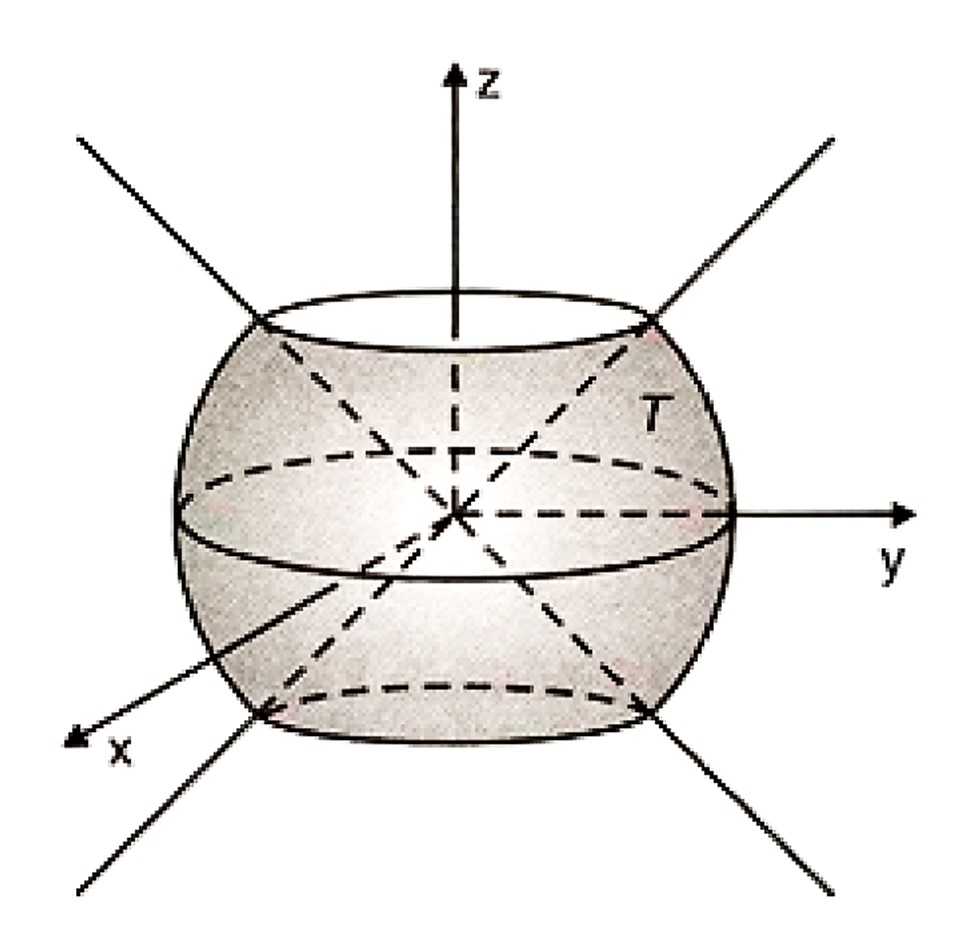
(d) f(x,y,z) = 1 e T é a região do espaço interior à esfera x^2 + y^2 +z^2 = 1 e exterior ao cone z^2 = x^2+y^2.

SOLUÇÃO: Na figura abaixo temos o sólido de integração T:

O sólido T pode ser escrito em coordenadas  como $$T: \left\{ \begin{array}{l} 0 \leq r \leq 1\\ 0 \leq \theta \leq \pi /2\\ \pi /4 \leq \phi \leq 3\pi /4\end{array} \right.$$

Portanto, $$\int \int \int\limits_{T}{1 dxdydz} = \int \int \int\limits_{T}{ r^2 sen(\phi) dr d \theta d \phi} = $$ $$ = \int\limits_{0}^{2 \pi } \int \limits_{\pi /4}^{3\pi /4} \int \limits_{0}^{1} {r^2 sen(\phi) dr d \phi d \theta} = 2 \pi \int \limits_{\pi /4}^{3\pi /4} \int \limits_{0}^{1} {r^2 sen(\phi) dr d \phi}= $$ $$ = \frac{2 \pi}{3}\int \limits_{\pi /4}^{3\pi /4} {sen(\phi) d \phi} = \frac{2 \sqrt{2} \pi}{3}$$

2) Calcule $$\iiint\limits_{T}e^{(x^2 + y^2 +z^2)^{3/2}} dxdydz,$$ onde T é a esfera unitária centrada na origem.

SOLUÇÃO: Como T é a esfera unitária centrada na origem, este sólido pode ser escrito analiticamente em coordenadas esféricas como $$ 0 \leq r \leq 1$$ $$0 \leq \theta \leq 2 \pi$$ $$0 \leq \phi \leq \pi .$$ Lembrando que em coordenadas esféricas $$ x^2 + y^2 +z^2 = r^2 $$ calculamos $$\iiint\limits_{T}e^{(x^2 + y^2 +z^2)^{3/2}} dxdydz = \iiint\limits_{T}e^{(r^2)^{3/2}} r^2 sen(\phi)drd \theta d \phi = \\ = \int\limits_{0}^{\pi} \int\limits_{0}^{2 \pi} \int\limits_{0}^{1}{ e^{(r^2)^{3/2}} r^2 sen(\phi)drd \theta d \phi} = \int\limits_{0}^{\pi}{sen(\phi) d \phi} \int\limits_{0}^{2 \pi} d \theta \int\limits_{0}^{1}{r^2 e^{r^3} dr } = \\ = \left[ -cos(\phi)  \right]_{0}^{\pi} \left( 2 \pi \right) \left[ \frac{1}{3}e^{r^3} \right]_{0}^{1} = \frac{4}{3} \pi ( e – 1 ).$$

Leia Mais:

• Integrais Triplas | 1ª Lista de Exercícios Resolvidos
• Mudança de Variável em Integrais Triplas | Coordenadas Cilíndricas e Esféricas
• As Integrais Triplas | Definição, Exemplos e Exercícios Resolvidos
• Como Calcular Volumes e Áreas com Integrais Múltiplas?

Assista Nossas Vídeo-Aulas: