Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano

Você está tendo dificuldade para entender a lógica dos vetores no plano cartesiano? Este guia ilustrado detalha tudo o que você precisa saber sobre matemática vetorial em duas dimensões.

Neste artigo, vamos mostrar uma forma de representar os segmentos orientados relacionados com os sistemas de eixos cartesianos no plano. Geometricamente, um vetor determinado por um segmento orientado AB é o conjunto de todos os segmentos orientados equipolentes a AB , como representado na figura abaixo.

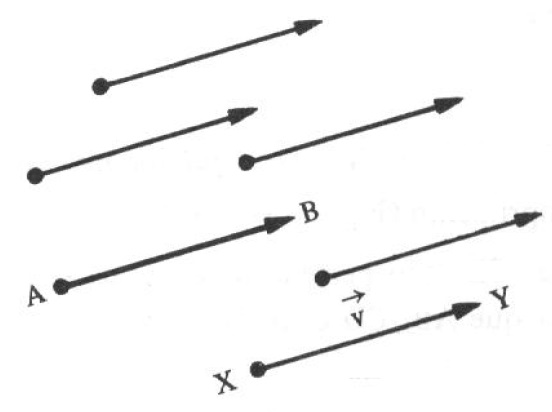
Se indicarmos como \vec{v} este conjunto, simbolicamente poderemos escrever: $$ \vec{v} = \left\{ XY; XY \sim AB \right\}$$ onde XY é um segmento qualquer do conjunto. O vetor determinado por AB é indicado por \vec{AB} ou B - A ou \vec{v} .

Portanto, um mesmo vetor \vec{AB} é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, e todos equipolentes entre si. Ou seja, todos com mesma direção, sentido e comprimento. O módulo de \vec{v} se indica por | \vec{v} | .

OBSERVAÇÃO:

1. Dois vetores   \vec{u} e   \vec{v} são colineares se tiverem a mesma direção, ou seja, se tiverem representantes pertencentes a uma mesma reta ou a retas paralelas.

   

2. Se os vetores não nulos   \vec{u} ,   \vec{v} e   \vec{w} possuem representantes pertencentes a um mesmo plano são ditos complanares. Dois vetores são sempre coplanares, mas três vetores poderão ou não ser coplanares.

   

A Decomposição de um Vetor no Plano

Dados dois vetores \vec{v_1} e \vec{v_2} , não colineares, E qualquer vetor \vec{v} (coplanar com \vec{v_1} e \vec{v_2} ). O problema consiste em determinar dois vetores cujas direções sejam as de \vec{v_1} e \vec{v_2} e cuja soma seja \vec{v} . Em outra palavras, iremos determinar dois números reais \alpha e \beta tais que  $$ \vec{v} = \alpha \vec{v_1} + \beta \vec{v_2} .$$

Neste caso, diremos que \vec{v} é uma combinação linear de \vec{v_1} e \vec{v_2} . Quando os dois vetores \vec{v_1} e \vec{v_2} , não colineares, é chamado base no plano. Aliás, qualquer conjunto \left\{ \vec{v_1} , \vec{v_2} \right\} de vetores não colineares constitui uma base no plano. Os números \alpha e \beta são chamados de componentes ou coordenadas de \vec{v} em relação à base \left\{ \vec{v_1} , \vec{v_2} \right\}.

Na prática, as bases mais utilizadas são as bases ortonormais, aquelas cujos vetores são unitários (ou seja, tem tamanho igual 1) e são ortogonais. Obviamente, quaisquer pares de vetores que satisfaçam estas condições são bases ortonormais, nos dando assim infinitas bases ortonormais. Porém, uma destas bases ortonormais é particularmente importante: a formada pelos vetores \vec{i} e \vec{j} , origem em 0 e extremidade nos pontos (1,0) e (0,1) . A base \left\{ \vec{i} , \vec{j} \right\}  é chamada de base canônica do plano \mathbb{R}^2 e é ilustrada abaixo:

A menos que em referência o contrário usaremos sempre a base canônica do plano. Dado um vetor $$ \vec{v} = x \vec{i} + y \vec{j} $$ no qual x e y são as componentes de \vec{v} em relação à base \left\{ \vec{i} , \vec{j} \right\}, sendo ilustrado abaixo.

Expressão Analítica de um Vetor

Fixada a base canônica \left\{ \vec{i} , \vec{j} \right\}, fica estabelecida uma correspondência biunívoca entre os vetores do plano e os pares ordenados (x,y) de números reais. Nestas condições definimos um vetor no plano como um par ordenado (x,y) de números reais representado por \vec{v} = (x,y) que é a expressão analítica de \vec{v} . A primeira componente x é chmada abscissa e a segunda, ordenada.

OBSERVAÇÃO: Deve ter ficado claro que a escolha proposital da base \left\{ \vec{i} , \vec{j} \right\} deve-se à simplificação. Assim, para exemplificar, quando nos referimos a uma ponto P(x,y) , ele pode ser identificado com o vetor \vec{v} = \vec{OP} = x \vec{i} + y \vec{j} , sendo O a origem do sistema como na figura abaixo:

Desta forma, o plano cartesiano pode ser encarado como um conjunto de pontos ou um conjunto de vetores.

Igualdade de Vetores

Dois vetores \vec{u} = \left( x_1 , y_1 \right) e \vec{v} = \left( x_2 , y_2 \right) são iguais se, e somente se, x_1 = x_2 e y_1 = y_2 , e escreve-se \vec{u} = \vec{v} .

EXEMPLOS:

1. Os vetores \vec{u} = \left(3 , 5 \right) e \vec{v} = \left( 3 , 5 \right) são iguais;
2. Se o vetor \vec{u} = \left( x + 1 , 4 \right) é igual ao vetor \vec{v} = \left( 5 , 2y-6\right) , de acordo com a definição de igualdade dos vetores x +1 = 5 e 2y -6 = 6 , ou seja, x = 4 e y = 5 . Assim, se \vec{u} = \vec{v} , então x = 4 e y = 5 .

Adição e Multiplicação por Escalar

Dados os vetores \vec{u} = \left( x_1 , y_1 \right) e \vec{v} = \left( x_2 , y_2 \right) e \alpha \in \mathbb{R} . Define-se:

$$ 1)\; \vec{u} + \vec{v} = \left( x_1 +x_2 , y_1 +y_2 \right); \qquad 2)\; \alpha \vec{u} = \left( \alpha  x_1 , \alpha y_1 \right),$$ que são, respectivamente, a soma de dois vetores e a multiplicação de um vetor por um escalar.

OBSERVAÇÕES:

• Geometricamente, determinar a soma de dois vetores consiste em “fechar o triângulo” definido pelo três pontos que os formam, tomando cuidado de escolher a origem do segundo coincidindo com a extremidade do primeiro representado da classe de segmentos orientados, Pode-se também adotar a “regra do paralelogramo” (dada neste artigo), que consiste me tomar representantes de \vec{u} e \vec{v}   com a mesma origem e construir um paralelogramo, com na figura abaixo. O segmento orientado gerado pela diagonal que vontem o ponto de origem dos dois vetores é um representate da soma dos mesmos dois vetores.
• A escolha do representante dos vetores \vec{u} e \vec{v} é arbitrária, mas isso não influi na determinação da soma destes dois vetores.
• Se \alpha \neq 0 e \vec{v} \neq \vec{0} , então o vetor \alpha \vec{v} é paralelo ao vetor \vec{v} ; os dois possuem o mesmo sentido se \alpha > 0 e sentidos opostos se \alpha < 0 . Além disso, o tamanho do vetor \alpha \vec{v} é igual ao tamanho do vetor \vec{v} multiplicado pelo módulo de \alpha ;
• É comum usar-se o termo escalar para designar um número real em contraposição a um vetor

EXEMPLO:

Dados os vetores \vec{u} = \left(4,1 \right) e \vec{v} = \left(2,6 \right) temos que $$ \vec{u} + \vec{v} = \left( 4+2 , 1+6 \right) = (6,7) $$ $$ 2 \vec{u} = 2 \left( 4,1\right) = \left( 8,2 \right) $$ Ambos estão ilustrados abaixo:

PROPRIEDADES DA ADIÇÃO DE VETORES

Para quaisquer vetores \vec{u} , \vec{v} e \vec{w} , tem-se

1. \vec{u} + \vec{v} = \vec{v} + \vec{u} ;
2. \vec{u} +  \left( \vec{v} + \vec{w} \right) = \left( \vec{u} + \vec{v} \right) + \vec{w} ;
3.   \vec{u} + \vec{0} = \vec{u} ;
4. \vec{u} + (- \vec{u}) = \vec{0} .

PROPRIEDADES DA MULTIPLICAÇÃO DE VETOR POR ESCALAR

Para quaisquer vetores \vec{u} e \vec{v} , e o números reais \alpha e \beta , tem-se

1. \alpha \left( \beta \vec{v} \right) = \left( \alpha \beta \right) \vec{v} ;
2. \left( \alpha + \beta \right) \vec{u} = \alpha \vec{u} + \beta \vec{u} ;
3. \alpha \left( \vec{u} + \vec{v}  \right) = \alpha \vec{u} + \alpha \vec{v} ;
4. 1 \vec{v} = \vec{v} .

OBSERVAÇÃO:

As quatro propriedades da adição e as quatro propriedades da multiplicação por escalar, conferem ao \mathbb{R} ^2 a estrutura do que chamamos de espaço vetorial;

A Soma de um Ponto comum Vetor

Dados um ponto P(x,y) e um vetor \vec{v} = ( a, b ) , existe um único segmento orientado \vec{PQ} que é representante de \vec{v} = ( a, b ) . Isso nos permite definir uma operação de que a cada ponto P \in \mathbb{R} ^2 e a a cada vetor \vec{v} \in \mathbb{R}^2 associa um único ponto Q \in \mathbb{R}^2 , indicado por Q = P + \vec{v} e chamado de soma de P com \vec{v} . Intuitivamente podemos encarar P + \vec{v} como o resultado de uma translação de ponto P , translação esta determinanda pelo vetor \vec{v} .

PROPRIEDADES DA SOMA DE UM PONTO COM VETOR:

Vejamos algumas propriedades desta operação:

1. P + \vec{0} = P ;
2. P + \vec{u} = P + \vec{v} \Rightarrow \vec{u} = \vec{v} ;
3. \left( P + \vec{u} \right) + \vec{v}= P + \left( \vec{u} + \vec{v} \right) ;

Vetor Definido Por Dois Pontos:

Inúmeras vezes um vetor é representado por um segmento orientado que não parte que não parte da origem do sistema. Considerando o vetor \vec{AB} de orgiem no ponto A(x_1, y_1) e extremidade em B(x_2,y_2) , as componentes de  \vec{AB} podem ser encontradas da seguinte maneira $$ \vec{AB}  = \left( x_2 – x_1 , y_2 – y_1 \right)$$ a razão pela qual também se escreve que $$ \vec{AB} = B – A .$$ Esta última é chamada de notação de Grassmann e não se trata à rigor de subtrair pontos, mas sim de uma notação sugestiva, já que o ponto B é a soma do ponto A com o vetor \vec{AB} . È melhor pensar que ela seria uma simplificação da notação $$ \vec{AB} = \vec{OB} – \vec{OA}$$ como nos infere a imagem abaixo:

É importante ressaltar que as componentes do vetor \vec{AB} , calculadas por meio de B - A , são sempre as mesmas componentes do segmento orientado da mesma classe que tem origem no início do sistema. Deixamos a figura abaixo como exemplo deste fato, onde os segmentos orientados \vec{AB}, \vec{CD} e \vec{OP} representam o mesmo vetor \vec{u} = (3,1) .

Condição de Paralelismo Entre Dois Vetores

Dois vetores \vec{u} = \left( x_1 , y_1 \right) e \vec{v} = \left( x_2 , y_2 \right)   são colineares (ou paralelos) se existe um número k \neq 0  tal que \vec{u} = k \vec{v} , ou seja, uma condição de paralelismo entre dois vetores é que suas componentes sejam proporcionais, ou seja $$ \frac{x_1}{x_2} = \frac{y_1}{y_2} = k .$$ Represenata-se por \vec{u} \parallel \vec{v} dois vetores \vec{u} e \vec{v} paralelos. É claro que se uma componente de um vetore é nula, a componente correspondente de um vetor paralelo também é nula.

EXEMPLO: Os vetores \vec{u} = (-2,3) e \vec{v} = (-4,6)   são paralelos, pois $$ \frac{-4}{-2} = \frac{6}{3} = 2.$$ Ou seja, $$ \vec{v} = 2 \vec{u}.$$

Leia Mais:

• O que é um Vetor? Um guia ilustrado dos vetores no espaço.
• O Espaço R²: Coordenadas no Plano Cartesiano
• Campos Vetoriais | Definição e Primeiros Exemplos
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula