O que é um Vetor? Um guia ilustrado dos vetores no espaço.

Você está tendo dificuldade para entender a lógica geométrica dos vetores? Este guia ilustrado detalha tudo o que você precisa saber sobre matemática vetorial.

Os vetores podem ser difíceis de entender. No entanto, com a abordagem correta e as técnicas de visualização, qualquer pessoa pode se sentir confortável com esse conceito matemático.

Neste guia, detalharemos os vetores no espaço e exploraremos suas propriedades por meio de ilustrações úteis, pois queremos apenas te apresentar a noção geométrica de vetor. Os vetores constituem uma importante ferramenta para o estudo da geometria analítica, da Físca, do Cálculo, etc. Você encontrará aqui as resposta para as perguntas:

1. O que é um vetor?
2. Como funciona um vetor?
3. Pra que serve um vetor?

Relembrando as notações de geometria clássica

Os nossos ambientes de estudo na geometria analítica serão o plano \mathbb{R} ^2 e o espaço \mathbb{R} ^3 , que de forma intuitiva devem ser enxergados como os espaços físicos que nos cercam.

Os pontos nestes ambientes serão indicados por letras latinas maiúsculas ( A , B, C, D, ... ); as retas por letras latinas minúsculas ( r, s, t, ... ) e os planos por letras gregas minúsculas ( \alpha , \beta, \gamma, \pi, ... ).

Se uma reta r contem os pontos P e Q , falaremos em “reta PQ “; o segmento geométrico de extremidades P e Q será indicado por PQ . Quando um plano contém o pontos P , Q e R não colineares, falaremos em “plano PQR .”

Definições importantes para entender o que é um vetor

Vetores são objetos matemáticos que possuem magnitude e direção. Eles são comumente usados ​​em física, engenharia e outros campos para descrever quantidades físicas como força e velocidade. Na geometria, eles são usados ​​para representar linhas e planos no espaço.

Compreender os vetores é essencial para muitos conceitos matemáticos avançados. Mas até definirmos o que é um vetor com o rigor matemático precisamos estabelecer conceitos necessários.

DEFINIÇÃO (reta orientada – eixo): Uma reta r é orientada quando se fixa nela um sentido de percurso, considerado positivo e indicado por uma seta como na figura abaixo. O sentido oposto é negativo. Uma reta orientada é denominada eixo.

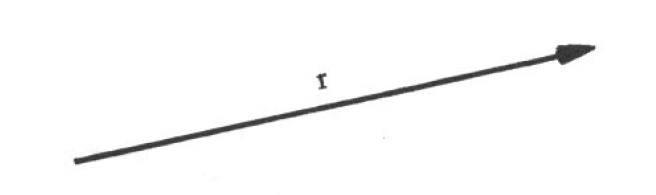
DEFINIÇÃO (segmento orientado): Um segmento orientado é um par odenado de pontos, o primeiro denominado origem e o segundo denominado extremidade. Um segmento orientado de origem A e extremidade B , será representado por AB e geometricamente será indicado por uma reta que caracteriza visualmente o sentido do segmento como na figura abaixo.

DEFINIÇÃO (Medida de um Segmento) Fixada uma unidade de comprimento, a cada segmento orientado pode-se associar um número real, não-negativo, que é a medida do segmento em relação àquela unidade. A medida do segmento orientado é seu comprimento ou seu módulo. O comprimento do segmento  AB é indicado por \overline{PQ} .

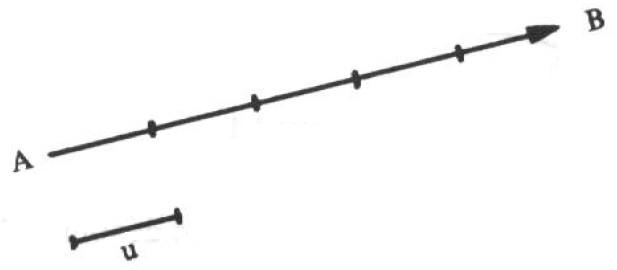
OBSERVAÇÕES

1. Um segmento nulo é aquele cuja extremidade coincide com a origem. Os segmentos nulos têm comprimento igual a zero;
2. Se AB é um segmento orientado, o segmento orientado BA é oposto de AB . O comprimento de segmentos opostos é igual.

DEFINIÇÃO (Direção e Sentido): Dois segmentos não nulos AB e CD tem mesma direção se as retas suportes desses segmentos são paralelas ou coincidentes.

OBERVAÇÕES: 

1. Só se pode comparar os sentidos de dois segmentos orientados se eles têm a mesma direção;
2. Dois segmentos orientados opostos têm sentidos contrários.

DEFINIÇÃO (Segmentos Equipolentes): Dois segmentos orientados AB e CD são equipolentes quando têm mesma direção, o mesmo sentido e o mesmo comprimento. 

OBSERVAÇÕES:

1. Dois segmentos nulos são sempre equipolentes;
2. A equipolência dos segmentos AB e CD é representada por $$ AB \sim CD.$$
3. Dado um segmento orientado AB e um ponto C , existe um único ponto D tal que AB \sim CD .

Enfim vamos definir o que é um vetor

Um vetor determinado por um segmento orientado AB é o conjunto de todos os segmentos orientados equipolentes a AB , como representado na figura abaixo.

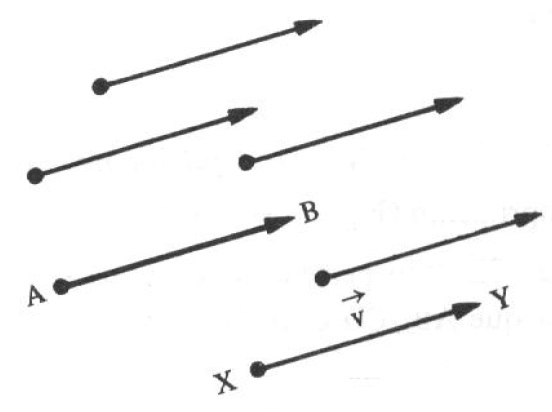
Se indicarmos como \vec{v} este conjunto, simbolicamente poderemos escrever: $$ \vec{v} = \left\{ XY; XY \sim AB \right\}$$ onde XY é um segmento qualquer do conjunto. O vetor determinado por AB é indicado por \vec{AB} ou B - A ou \vec{v} .

Portanto, um mesmo vetor \vec{AB} é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, e todos equipolentes entre si. Ou seja, todos com mesma direção, sentido e comprimento. O módulo de \vec{v} se indica por | \vec{v} | .

Os Principais Tipos de Vetores

1. Vetores Iguais: Dois vetores \vec{AB} e \vec{CD} são iguais se, e somente se, AB \sim CD ;
2. Vetor Nulo: Os segmentos nulos, por serem equipolentes entre si, determinam um único vetor, chamado vetor nulo ou vetor zero, que é indicado por \vec{0} ;
3. Vetores Opostos: Dado um vetor \vec{v} = \vec{AB} , o vetor \vec{AB} , o vetor \vec{BA} é o posto de \vec{AB} e se indica por - \vec{AB} ou por - \vec{v} .
4. Vetor Unitário: Um vetor  \vec{v} é unitário se  | \vec{v} | = 1 .
5. Versor: Dado um vetor não nulo   \vec{v} , o versor é o vetor unitário de mesma direção e mesmo sentido de \vec{v} . Na figura abaixo, o vetor \vec{ u_{1}} é o versor de   \vec{v} , pois mesmo  \vec{ u_{2}} sendo unitário e tendo a mesma direção de   \vec{v} , ele não tem seu sentido.

   

6. Vetores Colineares: Dois vetores   \vec{u} e   \vec{v} são colineares se tiverem a mesma direção, ou seja, se tiverem representantes pertencentes a uma mesma reta ou a retas paralelas.

   

7. Vetores Coplanares: Se os vetores não nulos   \vec{u} ,   \vec{v} e   \vec{w} possuem representantes pertencentes a um mesmo plano são ditos complanares. Dois vetores são sempre coplanares, mas três vetores poderão ou não ser coplanares.

Vetores coplanares e não-coplanares

A Soma de Vetores

Sejam os vetores   \vec{u} e   \vec{v} representados pelos segmentos orientados   \vec{AB} e   \vec{BC} como na figura abaixo.

Os pontos A e C determinam um vetor \vec{s} uqe é, por definição, a soma dos vetores   \vec{u} e   \vec{v} , isto é,   \vec{s} = \vec{u} + \vec{v} .

PROPRIEDADES DA ADIÇÃO DOS VETORES:

1. Comutativa: \vec{u} + \vec{v} = \vec{v} + \vec{u} ;
2. Associatica: \left( \vec{u} + \vec{v} \right) + \vec{w} = \vec{u} + \left( \vec{v} + \vec{w} \right) ;
3. O vetor \vec{0} é o vetor nulo da operação de adição, ou seja, \vec{v} + \vec{0} = \vec{v};
4. O vetor - \vec{v} é o vetor oposto de \vec{v} , ou seja,  \vec{v} + (- \vec{v} ) = \vec{0}.

A Diferença de Dois Vetores

Chama-se diferença de dois vetores   \vec{u} e   \vec{v} , e se representa por   \vec{d} = \vec{u} - \vec{v} , ao vetor   \vec{u} + \left( - \vec{v} \right) .

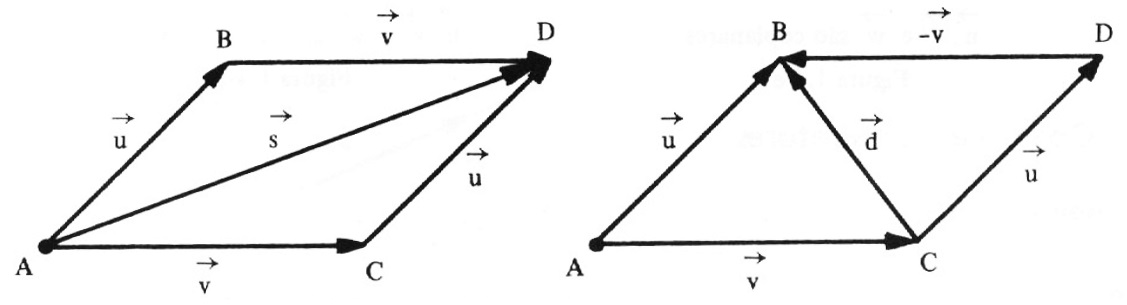
A Regra do Paralelogramo

Dados dois vetores   \vec{u} e   \vec{v} representados pelos segmentos orientados   AB e AC , respectivamente, e construído o paralelogramo   ABCD verifica-se que a soma   \vec{s} = \vec{u} + \vec{v} é representada pelo segmento orientado AD (uma das diagonais) e que a diferença   \vec{d} = \vec{u} - \vec{v} é representada pelo segmento orientado CB (a outra diagonal).

Multiplicação de Vetor por um Número Real

Dado um vetor \vec{v} \neq \vec{0} é um número real k \neq 0 , chama-se produto do número real  k  pelo vetor  \vec{v} o vetor \vec{p} = k \vec{v} , tal que:

1. módulo: | \vec{p} | = | k |  | \vec{v} | ;
2. direção: a mesma de \vec{v} ;
3. sentido: o mesmo de \vec{v} se k > 0 e oposta a de \vec{v} se k < 0 .

PROPRIEDADES DO PRODUTO DE VETORES POR NÚMERO REAL:

Dados dois vetores   \vec{u} e   \vec{v} e   a e   b dois números reais, temos:

1. a ( b \vec{v} ) = (ab) \vec{v} ;
2. (a + b) \vec{v} ) = a \vec{v} + b \vec{v};
3. a ( \vec{u} + \vec{v} ) = a \vec{u} + a \vec{v};
4. 1 \vec{v} = \vec{v} .

O Ângulo de Dois Vetores

O ângulo de dois vetores   \vec{u} e   \vec{v} não nulos é o ângulo \theta formado pelas semi-retas OA e OB , tal que 0 \leq \theta \leq \pi , como na figura abaixo:

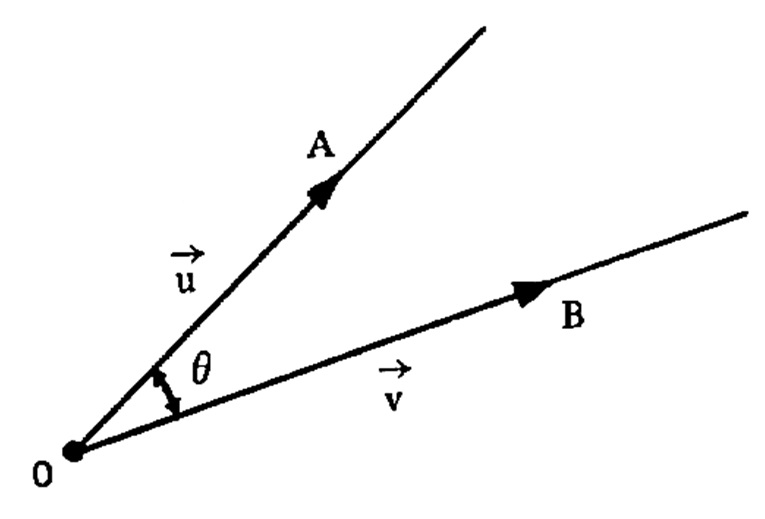
OBSERVAÇÕES:

1. Se \theta = \pi , então   \vec{u} e   \vec{v} têm a mesma direção e sentidos opostos;
2. Se \theta = 0 , então   \vec{u} e   \vec{v} têm a mesma direção e o mesmo sentido;
3. Se \theta = \dfrac{\pi}{2} , então   \vec{u} e   \vec{v} são ortogonais e indica-se \vec{u} \bot \vec{v} ; Neste caso, o triângulo retângulo OBC permite escrever $$ | \vec{u} + \vec{v} | ^2 = | \vec{u} | ^2 + | \vec{v} |^2 .$$
4. O vetor nulo é ortogonal a qualquer vetor;
5. Se   \vec{u} é ortogonal a   \vec{v} e m é um número real qualquer,   \vec{u} é ortogonal a   m \vec{v} .
6. O ângulo formado pelos vetores   \vec{u} e - \vec{v} é o sulemento do ângulo de   \vec{u} e   \vec{v} , como na figura abaixo:

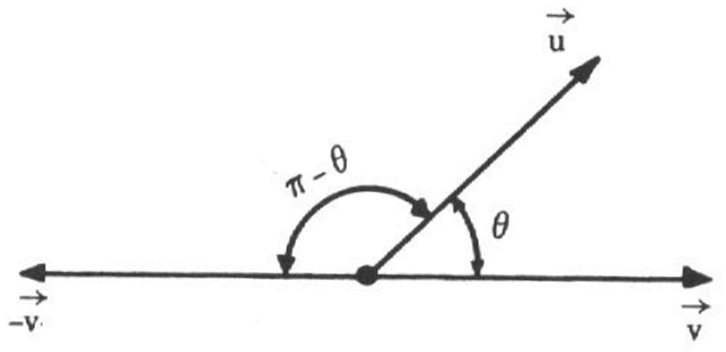Leia Mais Artigos Sobre Vetores:

• Vetor Gradiente | Definição, Campo Gradiente e Exercícios Resolvidos
• Campos Vetoriais | Definição e Primeiros Exemplos