Integrais Elípticas | Funções Hiperbólicas e Comprimento de Arco

As Integrais Elípticas estão ligadas ao comprimento de arco de uma elipse, à determinação do período do pêndulo simples e à deflexão de uma barra elástica fina, que são alguns dos problemas encontrados no tempo em que é exigida a integração de funções irracionais para a sua solução.

Como não é possível avaliar estas integrais em termos de funções elementares, eram obtidos resultados úteis em termos de séries infinitas, aproximações ou relacionando com o teorema de adição devido à Euler.

Um Pouco da História

A historia das Integrais Elípticas e das Funções Elípticas de Jacobi está ligada a matemáticos como Legendre, Abel e Jacobi.

Adrien Marie Legendre

Adrien Marie Legendre foi um matemático Frances nasceu em 1752, viveu em Paris e faleceu em 1833. Seus principais trabalhos em matemática superior concentram-se em teoria dos números, funções elípticas, o método dos mínimos quadrados e integrais. E também conhecido na historia da matemática.

O trabalho Exercises Du Calcul Intégral foi um dos grandes trabalhos de Legendre sobre funções elípticas, onde ele apresentou as propriedades básicas das integrais elípticas, bem como suas tabelas e também das funções beta e gama.

E no trabalho Fonctions Traité des Elliptiques, reorganizou este material. Passou 40 anos trabalhando em funções elípticas, mas foi ofuscado pelos trabalhos de Abel e Jacobi.

Niels Henrik Abel

Niels Henrik Abel nasceu em Findö na Noruega, em 1802. De família pobre, estudou na Universidade de Oslo com a ajuda de professores. Obteve uma bolsa que lhe permitiu viajar para a Alemanha, a Itália e a França e escreveu diversos artigos em matemática.

Em 1827, no segundo volume do Journal de Crelle Abel apresentou o trabalho “Teoria das Funções Duplamente Periódicas”. Como Legendre era pioneiro no desenvolvimento das funções elípticas ficou admirado com as descobertas de Abel, as quais foram realizadas concomitantemente a Jacobi.

Abel apresentou uma dissertação sobre integrais de funções algébricas, só publicada 12 anos após sua morte. Com pouca idade, descobriu que sofria de tuberculose, mas prosseguiu com suas pesquisas até a morte, em 1829.

Abel não teve o reconhecimento devido em vida, contudo postumamente foi nomeado professor da Universidade de Berlim e ganhou um prêmio do Instituto Francês em 1841, por seus trabalhos com Funções Elípticas.

Carl Gustav Jakob Jacobi

No século XIX a Matemática era basicamente ligada à mecânica e à astronomia e Carl Gustav Jakob Jacobi e outros, foram os notáveis matemáticos que deram um novo impulso as atividades matemáticas fazendo-a avançar, na Alemanha.

Jacobi nasceu em Potsdam em 1804 e era descendente de judeus. Em 1825 obteve seu doutorado na Universidade de Berlim e trabalhou como respeitável professor em Königsberg.

Em 1842, com uma pensão do governo da Prússia, abdicou à sua cadeira em Königsberg e mudou-se para Berlim, onde viveu até 1851, ano de sua morte.

Entre as obras de Jacobi, é notável sua pesquisa que trata das funções elípticas, ele pesquisou simultaneamente ao matemático norueguês Abel e os resultados acordados, embora de forma totalmente independente, lançaram as bases da teoria destas funções.

Jacobi com o trabalho “Fundamenta nova theoria functionum el lipticarum”, em 1829, ano da morte de Abel, conseguiu atrair a atenção de toda a comunidade matemática e mereceu elogios até de Legendre.

Este sucesso deveu-se a crucial ideia de iniciar suas descobertas com a inversão das integrais elípticas.

Com as profundas descobertas no estudo de funções elípticas Jacobi alcançou o seu lugar como um dos maiores matemáticos da época e deixou contribuições importantes que abrangem quase todas as áreas da matemática.

Jacobi merece crédito por vários teoremas centrais relacionados com funções elípticas. A ele também devemos o estudo das “funções theta de Jacobi”, funções inteiras das quais as elípticas são quocientes.

Do Comprimento de Arco da Elipse à Integral Elíptica

As integrais elípticas estão intimamente ligadas ao cálculo do comprimento de arco da elipse com eixos com medidas a,b>0 sobre os eixos coordenados e centrada na origem, e foram inicialmente estudadas por Giulio Carlo Fagnano dei Toschi e Leonhard Euler.

Como a parametrização da elipse $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ é dada por $$ \gamma (t) = (a cos(t), b sen(t)),$$ então o comprimento de arco dessa elipse é dada por $$ s(t) = \int_{0}^{2 \pi}{\sqrt{a^2 sen^2 (t) + b^2 cos^2 (t)} dt}.$$

Esta integral está intimamente ligada às integrais conhecidas como Integrais Elípticas.

Em geral, integrais elípticas não podem ser expressas em termos de funções elementares, exceto em casos particulares.

Contudo, com apropriadas reduções de fórmulas, cada integral elíptica pode ser quebrada em uma forma que envolve integrais sobre funções racionais, e as três formas canônicas (isto é, uma integral elíptica de primeira, segunda ou terceira forma).

Uma integral na forma $$\int{ \frac{dx}{\sqrt{1 – k^2 sen^2 (x)}} dx}, \;\;\; 0 < k^2 < 1 $$ é um exemplo de uma integral elíptica. Isso pode ser mostrado que esta integral não pode ser calculada em termos de funções elementares.

Desta forma, alguns métodos numéricos são usados nos estudos desta equação.

Por causa da importância destas integrais em aplicações, foram elaboradas algumas tabelas computadas pela função

$$y = F(x) = \int_{0}^{x}{ \frac{dt}{\sqrt{1 – k^2 sen^2 (t)}}}.$$

para vários valores da constante k. 

Esta integral é denominada Integral Elíptica de Primeira Espécie.

Funções Circulares e Hiperbólicas

As funções elípticas de Jacobi são definidas como as inversas da integral elíptica de primeira espécie, que são dada por $$u(x) = \int_{0}^{x}{ \frac{dt}{\sqrt{(1 – k^2 t^2)(1-t^2)}}} .$$

Veremos que as funções elípticas reduzem-se às funções circulares quando k=0 e às funções hiperbólicas quando k = 1, considerados casos degenerados destas funções.

FUNÇÕES CIRCULARES:

Delinearemos as propriedades das funções elípticas quando estas se reduzem ao círculo, ou seja, quando k=0 em $$u(x) = \int_{0}^{x}{ \frac{dt}{\sqrt{(1 – k^2 t^2)(1-t^2)}}} ,$$ donde obtemos $$u(x) = \int_{0}^{x}{ \frac{dt}{\sqrt{(1-t^2)}}} .$$

A integral indefinida deste caso é tabelada (como nessa tabela de integrais) e é dada por $$u(x) = \int{ \frac{dt}{\sqrt{(1-t^2)}}} = arcsen(t).$$

Desta forma, definimos uma função bijetora u: [-1,1] \rightarrow [- \pi /2 , \pi /2]   tal que $$u(x) = arcsen(x) .$$

À partir daqui podemos estabelecer todas as definições e propriedades das funções trigonométricas.

FUNÇÕES HIPERBÓLICAS:

Delinearemos as propriedades das funções elípticas quando estas se reduzem ao círculo, ou seja, quando k=1 em $$u(x) = \int_{0}^{x}{ \frac{dt}{\sqrt{(1 – k^2 t^2)(1-t^2)}}} ,$$ donde obtemos $$u(x) = \int_{0}^{x}{ \frac{dt}{1-t^2}} .$$

Suponha (1 - t^2) > 0 . Pela tabela de integração a integral acima determina uma função  bijetora u: [-1,1] \rightarrow [- \infty , + \infty]   tal que $$u(x) = arctgh(x) .$$

Logo, x = tgh(u) , que é a tangente hiperbólica de u.

As funções hiperbólicas podem ser expressas em termos de e^x , assim como as funções hiperbólicas inversas podem ser expressas e termos dos logaritmos naturais.

De fato, podemos expressar a solução de $$u(x) = \int_{0}^{x}{ \frac{dt}{1-t^2}}$$ como $$ u = \frac{1}{2} ln \left| \frac{1+x}{1-x} \right| ; \;\;\;se\;\;\; u \neq 1$$

Integrais Elípticas de Segunda e Terceira Espécies

Já as integrais deste tipo são ilustradas por $$y =E(x) = \int_{0}^{x}{\sqrt{1 – k^2 sen^2 (t)} dt},$$

$$y = \int_{0}^{x}{ \frac{dt}{\sqrt{1 – k^2 sen^2 (t)} (1 + a^2 sen^2 (t))}},$$

onde 0 < k^2 < 1, a \neq 0, a^2 \neq k^2 são denominadas Integral Elíptica de Segunda Espécie e Integral Elíptica de Terceira Espécie, respectivamente.

A integral $$y =E(x) = \int_{0}^{x}{\sqrt{1 – k^2 sen^2 (t)} dt}$$ surge no cálculo do comprimento de arco de uma elipse e esta é a base do termo Integral Elíptica.

Pode ser mostrado que se R(x,y) é uma função racional  de x e y e g(x) é um polinômio de x de grau 3 ou 4, então a integral $$ \int{R \left[x, \sqrt{g(x)} \right] dx}$$ pode ser expressa como uma função elementar adicionada de integrais elípticas de primeira, segunda ou terceira espécie.

Ou seja, em geral, integrais elípticas não podem ser expressas em termos de funções elementares; exceto quando P tem raízes repetidas, ou quando R(x,y) não contem nenhuma potência de ordem ímpar de y na integral elíptica de segunda espécie

Desta forma, métodos numéricos de algumas integrais permitem precisamente calcular um grande classe de integrais.

Isto adiciona enfase ao fato de que cada integral indefinida determina uma função de x.  Para cada nova integral indefinida que estudamos e calculamos, uma grande classe de novas funções que são numericamente manipuláveis e abertas a minuciosas análises

Uma Aproximação Para a Integral Elíptica de Segunda Espécie

Dada a importância da Integral Elíptica de Segunda Espécie $$E(x) = \int_{0}^{x}{\sqrt{1 – k^2 sen^2 (t)} dt},$$ podemos expressá-la em termos de funções elementares expandindo o integrando através de uma série binomial.

Lembrando da expansão binomial $$ (1+x )^n = 1 + nx + \frac{n(n-1) x^2}{2!} + \frac{n(n-1) (n-2) x^3}{3!} + \frac{n(n-1) (n-2) (n-3) x^4}{4!} +… $$ podemos escrever, fazendo n = 1/2 e x = -k^2 sen^2 (t) , uma expressão dada por:

$$ (1 – k^2 sen^2(t)) ^{1/2} = 1 – \frac{k^2 sen^2 (t)}{2} \frac{k^4 sen^4 (t)}{8} – \frac{k^6 sen^6 (t)}{16} +… $$

Ou seja, truncando a expansão em algum grau e calculando a integral termo a termo, conseguimos aproximações para calcular o comprimento de uma elipse em função de sua excentricidade e seu eixo maior.

 

Exemplo 1

$$ \int{\frac{x}{\sqrt{(1 – k^2 x^2)(1-x^2)}}dx} = ?$$

Neste caso, fazemos t = x^2 , o que implica que x = \sqrt{t} e dx = \dfrac{1}{2 \sqrt{t}} dt ficamos com $$ \int{\frac{x}{\sqrt{(1 – k^2 x^2)(1-x^2)}}dx} = \frac{1}{2} \int{\frac{1}{\sqrt{(1 – k^2 t)(1-t)}}dx}.$$ Usando a Tabela de Derivadas e Integrais obtemos $$ \int{\frac{x}{\sqrt{(1 – k^2 x^2)(1-x^2)}}dx} = \frac{1}{2} \int{\frac{1}{\sqrt{(1 – k^2 t)(1-t)}}dx} = \frac{1}{k} log \left[ \sqrt{1 – k^2 t} – k \sqrt{1-t}\right].$$

Exemplo 2 (O Comprimento da Elipse)

Como a parametrização da elipse $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ é dada por $$ \gamma (t) = (a cos(t), b sen(t)),$$ então o comprimento de arco dessa elipse é dada por $$ L = \int_{0}^{2 \pi}{\sqrt{a^2 sen^2 (t) + b^2 cos^2 (t)} dt}.$$

Como a excentricidade da elipse é dada por 0 \leq k \leq 1 , facilmente podemos escrever $$ L = \int_{0}^{2 \pi}{\sqrt{a^2 sen^2 (t) + b^2 cos^2 (t)} dt} = a \int_{0}^{2 \pi}{\sqrt{1 – k^2 sen^2 (t)} dt}.$$

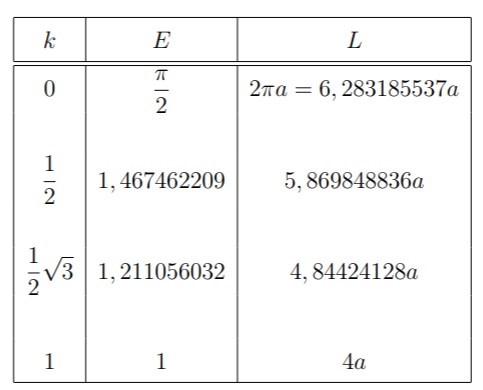
Agora, observando que $$ L = a \int_{0}^{2 \pi}{\sqrt{1 – k^2 sen^2 (t)} dt} = 4 a  \int_{0}^{\pi / 2}{\sqrt{1 – k^2 sen^2 (t)} dt} = 4 a E(k), $$ onde E(k) é a integral elíptica de segunda espécie.

Lembre-se que quanto maior for a excentricidade, mais achatada será a elipse.

Usando técnicas numéricas para calcular a integral elíptica para alguns valores de 0 \leq k \leq 1 encontramos a tabela:

Referências:

1. Kaplan, Wilfred. Advanced Calculus, 5ª Edition. Pearson, 2002.
2. Simão, Cleonice Salateski. Uma Introdução ao Estudo das Funções Elípticas de Jacobi. 2013. (Leia aqui)

Leia Mais:

• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Curvas no Espaço | Funções de uma Variável Real a Valores Vetoriais
• Curvas no Espaço | Lista de Exercícios Resolvidos
• Tabela de Derivadas e Integrais
• Integração por Frações Parciais | Técnicas de Primitivação
• EFEITO BORBOLETA | Edward Lorenz e a Teoria do Caos
• GRÁFICOS | Da Análise Estatística ao Mercado de Ações 
• Apocalipse | A Ciência do Fim do Mundo 
• Universos Paralelos: Ciência ou Ficção Científica?