Teoremas de Stokes e da Divergência | 1ª Lista de Exercícios Resolvidos

Neste artigo queremos apresentar uma lista de exercícios envolvendo os clássicos teoremas de Stokes e da Divergência, responsáveis por amarrar as Integrais de Superfície às Integrais Triplas e Integrais de Linha.

O Teorema de Stokes é, na verdade, uma generalização do Teorema de Green para o espaço tridimensional e pode ser utilizado para transformar determinadas integrais curvilíneas em integrais de superfície ou vice-versa. Já o Teorema da Divergência, ou de Gauss, expressa uma relação entre uma integral tripla sobre um sólido e uma integral de superfície sobre a fronteira desse sólido.

Ambos sendo de grande importância em aplicações físicas. O Teorema da Divergência, por exemplo, tem aplicações básicas no fluxo de fluidos, onde ele auxilia a caracterizar fontes e locais de escoamento do fluido. Já na condução de calor, ele modela a equação básica do calor e na teoria potencial esse teorema dá propriedades básicas das soluções da Equação de Laplace.

Para ter um enunciado rigoroso, com exemplos e observações pertinentes sobre os Teoremas de Stokes e da Divergência, leia este nosso artigo especial sobre os dois e as integrais de superfícies.

Teoremas de Stokes e da Divergência | 1ª Lista de Exercícios Resolvidos

1) Use o Teorema de Stokes para calcular a integral $$\iint\limits_{S} rot \vec{f} \cdot dS,$$ onde $$ \vec{f} (x,y,z) = xz \vec{i} +yz \vec{j} + xy \vec{k} $$ e S é a parte da esfera x^2 + y^2 + z^2 = 4 que está dentro do cilindro x^2 + y^2 = 1 e acima do plano-xy (ilustrada na figura abaixo).

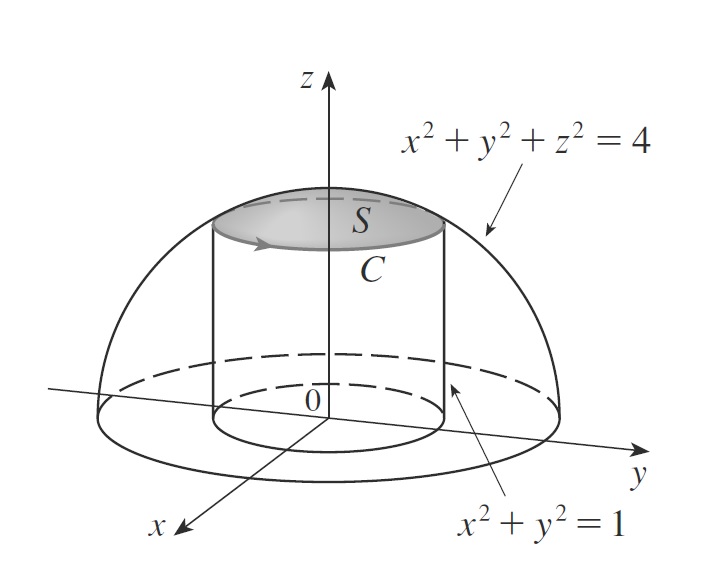
SOLUÇÃO: Para encontrar a curva C que é interseção do cilindro com a esfera  basta resolver o sistema entre as equações x^2 + y^2 +z^2 = 4 e x^2 + y^2 = 1 que nos leva ao círculo de equações dadas por $$x^2 + y^2 = 1 $$ $$z = \sqrt{3} .$$ Desta forma, equação do vetorial de C é dada por $$ \vec{r} (t) = cos(t) \vec{i} +sen(t) \vec{j} + \sqrt{3} \vec{k}; \qquad 0 \leq t \leq 2 \pi,$$ o que nos leva a $$ \vec{r} ‘ (t) = – sen(t) \vec{i} +cos(t) \vec{j}.$$ Além disso, nós temos $$ \vec{f} \left( \vec{r} (t) \right) = \sqrt{3} cos(t) \vec{i} + \sqrt{3} sen(t) \vec{j}+ sen(t) cos(t) \vec{k} .$$

Portanto, pelo Teorema de Stokes $$ \iint\limits_{S} rot \vec{f} \cdot dS = \int\limits_{C}{\vec{f} \cdot d \vec{r}} =$$ $$ = \int\limits_{0}^{2 \pi}{ \vec{f} \left( \vec{r} \right) \cdot  \vec{r}’ dt} = $$ $$=\int\limits_{0}^{2 \pi}{ [- \sqrt{3} cos(t) sen(t)  +\sqrt{3} sen(t) cos(t) ]dt } = \int\limits_{0}^{2 \pi}{0 dt} = 0.$$

2) Encontre o fluxo do campo vetorial $$ \vec{f} (x,y,z) = z \vec{i} +y \vec{j} + x \vec{k} $$ sobre a esfera unitária $$x^2 + y^2 + z^2 = 1.$$

SOLUÇÃO: Para resolver este problema usaremos o Teorema da Divergência. Primeiro calculamos o divergente de \vec{f} (x,y,z) = z \vec{i} +y \vec{j} + x \vec{k} : $$ \text{div} \vec{f} = \frac{\partial }{\partial x} (z)+\frac{\partial }{\partial y} (y)+\frac{\partial }{\partial z} (x) =1 . $$

A esfera unitária S é limitada pela bola $$B: x^2 + y^2 + z^2 \leq 1 .$$ Portanto, o teorema da divergência nos dá o fluxo como $$ \iint\limits_{S} \vec{f} \cdot d\vec{S} = \iiint\limits_{B}\text{div} \vec{f} dV = \\ \iiint\limits_{B} 1 dV = V(B) = \frac{4}{3} \pi (1)^3 = \frac{4}{3} \pi .$$

Leia Mais:

• Introdução às Superfícies: Parametrização, Suavidade e Cálculo de Área.
• Integral de Superfície | Campos Escalares, Campos Vetoriais e Fluxos
• Integral de Linha de 1ª e 2ª Espécies | Teorema de Green no Plano
• Integrais Duplas | Funções de Várias Variáveis
• As Integrais Triplas | Funções da Várias Variáveis
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula.

Assista Nossas Vídeo-Aulas Sobre os Teoremas de Stokes e da Divergência