Série de Fourier | História, Definição e Condições de Convergência.

Neste artigo queremos investigar as Séries de Fourier, partindo de sua história, passando pela sua definição e as condições de convergência, conhecidas como Condições de Dirichlet.

As Séries de Fourier que são largamente utilizadas na resolução de muitos problemas de valores de contorno, cujas soluções, para serem encontradas, é necessário conhecer o desenvolvimento de uma função em uma série trigonométrica.

Seja f(x) definida num intervalo (-L,L) e periódica com período igual a 2L.

Queremos determinar uma expansão em série de f(x) na forma $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right),$$ onde os termos a_n e b_n, denominados coeficientes de Fourier de f(x), são dados por

$$a_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{n\pi x}{L} \right)} dx} $$ e $$b_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$ para n=1,2,3,4,....

Note que por causa da periodicidade dos integrandos, o intervalo de integração para os coeficientes de Fourier podem ser substituídos por qualquer outro intervalo de tamanho 2L, por exemplo, o intervalo [0, 2L].

Um Pouco de História das Séries de Fourier

Em 21 de dezembro de 1807, um engenheiro chamado Joseph Fourier anunciou à prestigiada Academia Francesa de Ciências que uma função arbitrária f(x) poderia ser expandida em uma série infinita de senos e cossenos.

Em suas pesquisas sobre a condução do calor, Fourier foi levado à notável descoberta destas séries trigonométricas e desde então as séries de Fourier, bem como suas generalizações imediatas paras as integrais de Fourier e séries ortogonais, tornaram-se parte essencial do cabedal de cientistas, engenheiros e matemáticos, quer do ponto de vista teórico, quer quanto às aplicações.

O anúncio de Fourier causou um alvoroço na Acadêmia, muitos de seus membros mais proeminentes como Lagrange encararam o fato como absurdo baseado no fato de que naquele tempo esta afirmação não podia ser fundamentada com o rigor matemático necessário.

De toda forma, vários matemáticos vieram desenvolvendo o que ficou conhecida como teoria das Séries de Fourier que várias obras foram publicadas sobre o assunto.

Somente recentemente, de fato, foi possível estabelecer critérios para a convergência das séries de Fourier sendo este resultado um dos mais importantes teoremas da matemática no século XX.

As Condições de Dirichlet.

Note que que a série descrita na forma $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right),$$ é apenas a série de Fourier de f(x), não podendo garantir, apenas pela definição se a mesma converge, e mais, se ela converge para f(x).

Para nos certificarmos disso usamos as Condições de Dirichlet.

QUEM FOI DIRICHLET?

Peter Gustav Lejeune Dirichlet, (1805 – 1859) foi um matemático alemão que fez contribuições valiosas para a teoria dos números, análise e mecânica.

Ele lecionou nas universidades de Breslau (1827) e Berlim (1828-55), e em 1855 sucedeu Carl Friedrich Gauss na Universidade de Göttingen.

Dirichlet fez contribuições notáveis ​​ainda associadas ao seu nome em muitos campos da matemática.

Em 1837, Dirichlet propôs o conceito moderno de uma função y = f (x) na qual, para cada x, está associado um único y.

Em mecânica, ele investigou o equilíbrio dos sistemas e a teoria do potencial, o que o levou ao problema de Dirichlet relativo às funções harmônicas com valores de fronteira prescritos.

TEOREMA [CONDIÇÕES DE DIRICHLET]

Suponhamos que:

1. 1. f(x) seja definida, exceto possivelmente em um número finito de de pontos do intervalo (-L,L).
   2. f(x) seja periódica de período 2L.
   3. f(x) e f'(x) sejam seccionalmente contínuas em (-L,L).

Então a série $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$

com coeficientes dados por $$a_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{n\pi x}{L} \right)} dx} $$ e $$b_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$ converge para

1. 1. f(x) se x é ponto de continuidade;
   2. \frac{f(x+0) + f(x-0) }{2} se x é ponto de descontinuidade, sendo f(x+0) o limite de f(x) à direita de x e f(x-0) o limite de f(x) à esquerda de x.

É importante salientar que nem sempre a série de Fourier converge para f(x).

Em alguns casos ela pode até mesmo divergir.

Além disso, as condições impostas pelo teorema acima são condições suficientes, mas não necessárias , ou seja, mesmo se elas não forem satisfeitas a série poderá convergir ou não.

As condições em questão são, em geral, satisfeitas nos problemas que surgem na ciência ou na engenharia. 

Não conhecemos ainda, condições que sejam necessárias e suficientes para a convergência das Séries de Fourier. É conveniente notar que a continuidade de f(x) , por si só, não garante a convergência de uma série de Fourier.

No caso da convergência da Série de Fourier para a função f(x) diremos que a série $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ é representação de f(x) por sua série de Fourier.

Rápida Interpretação Geométrica.

Geometricamente, o que a Série de Fourier faz é aproximar uma função periódicas por uma soma infinita de senos e cossenos.

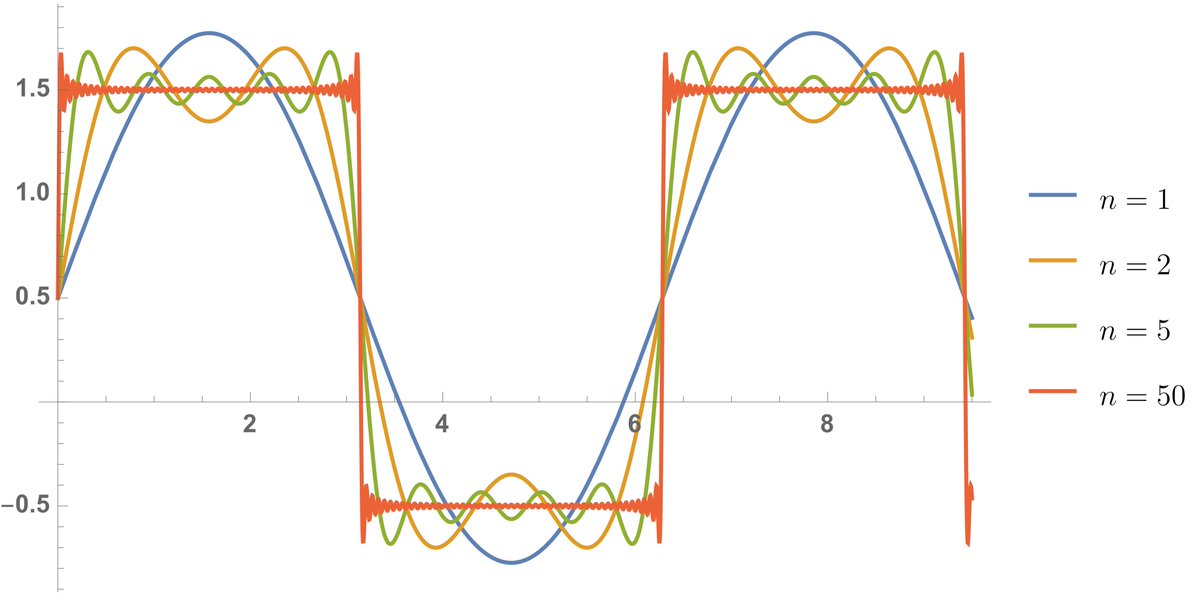
Abaixo, você tem uma ilustração de como isso é feito à partir das sucessivas somas de n=1,2,3,4,…

Observe que para n=1 a aproximação é ruim, mas à medida que as somas vão aumentando a aproximação vai se refinando e para n=50, visualmente, já temos uma aproximação quase perfeita da onda quadrada.

Agora use seu poder de abstração e imagine o que acontece quando n aumenta indefinidamente.

Obviamente, esbarramos nos custo computacional para isso, mas como motivação intelectual é uma ótima forma de pensar a Série de Fourier.

EXEMPLIFICANDO A SÉRIE DE FOURIER

Considere $$f(x) = \left\{ \begin{array}{ccl}
0 & ;& -1\leq x <0\\
1 & ;& 0 \leq x \leq 1\\
f(x+2) & = & f(x)
\end{array} \right.$$

Note que esta função é definida e todos os pontos e seccionalmente contínua no intervalo (-1,1) e sua derivada é dada por $$f(x) = \left\{ \begin{array}{rll}
0 & ;& -1\leq x <0\\
0 & ;& 0 < x \leq 1
\end{array} \right.$$ que também é uma função seccionalmente contínua no intervalo (-1, 1) e ainda, f é periódica de período igual a 2.

Pelas condições de Dirichilet

$$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ onde

$$a_0 = \int\limits _{-1}^{1}{f(x) \cos{\left( \frac{n\pi x}{1} \right)} dx} = 1$$

$$a_n = \int\limits _{-1}^{0}{ 0 \cos{\left( \frac{n\pi x}{L} \right)} dx} + \int\limits _{0}^{1}{ \cos{\left( \frac{n\pi x}{L} \right)} dx} = 0$$

e

$$b_n = \int\limits _{-1}^{0}{ 0 \sin{\left( \frac{n\pi x}{L} \right)} dx} + \int\limits _{0}^{1}{ \sin{\left( \frac{n\pi x}{L} \right)} dx} =
\left\{\begin{array}{cll}
0; & n\;\;\;é\;\;\;par\\
\frac{2}{n \pi}; & n\;\;\;é\;\;\;ímpar\\
\end{array} \right.$$

O que nos leva a

$$ f(x) = \frac{1}{2} + \frac{2}{ \pi } \sum\limits_{n=1}^{\infty} \frac{1}{2n-1}  \sin{\left((2n-1)\pi \right)}, $$ se lembrarmos que todos os números ímpares podem ser escritos na forma (2n-1) se n = 1,2,3,4,….

Esta aproximação é representada na figura abaixo:

A Notação Complexa da Série de Fourier

Utilizando as identidades de Euler $$ e^{i \theta} = cos \theta + i sen \theta, \qquad e^{-i \theta} = cos \theta – i sen \theta $$ onde i é a unidade imaginária tal que i^2 = -1 , podemos escrever a série de Fourier para f(x) sob a forma complexa como $$f(x) =  \sum\limits_{ – \infty}^{+ \infty}{c_n e^{\frac{i n \pi x}{L}}}$$ onde $$ c_n = \frac{1}{2L}\int\limits_{-L}^{L}{f(x) e^{\frac{- i n \pi x}{L}} dx } .$$

Ao escrevermos esta forma complexa da Séries de Fourier, estamos admitindo satisfeitas as condições de Dirichlet e também que f(x) seja contínua em x . Se f(x) é descontínua em x , o membro esquerdo desta forma complexa deve ser substituído por \frac{f(x+0) + f(x-0) }{2} , sendo f(x+0) o limite de f(x) à direita de x e f(x-0) o limite de f(x) à esquerda de x.

Séries Duplas de Fourier

A ideia de desenvolver em série de Fourier uma função de uma variável pode ser generalizada para o caso de funções de duas variáveis x e y , isto é, f(x,y) .

Por exemplo, podemos desenvolver f(x,y) em série dupla de Fourier de senos $$ f(x,y) = \sum\limits_{m=1}^{+ \infty} \sum\limits_{n=1}^{+ \infty}{B_{mn} sen \left( \frac{m \pi x}{L_1} \right) sen \left( \frac{n \pi y}{L_2} \right)}$$ onde $$ B_{mn} = \int\limits_{0}^{L_1} \int\limits_{0}^{L_2}{f(x,y) sen \left( \frac{m \pi x}{L_1} \right) sen \left( \frac{n \pi y}{L_2} \right) dxdy}$$

Podemos obter resultados análogos para as séries de cossenos, ou para séries envolvendo senos e cossenos.

Além disso, esta ideia pode ser generalizada para séries n-ésimas de Fourier como desenvolvimento de uma função de várias variáveis.

Aplicações das Séries de Fourier

São numerosas as aplicações das séries de Fourier à resolução de problemas de valores de contorno.

Alguns exemplos clássicos são:

1. Fluxo do Calor
2. Equação de Laplace
3. Sistemas Vibrantes.

Conclusões Sobre a Série de Fourier

Em outras palavras, a expansão de uma função periódica em série de Fourier equivale a decomposição da função em termos de suas componentes em várias frequências, ou seja, um sinal periódico apresenta um espectro de frequência discreto e infinito.

O espectro de frequência discreto aparece em um gráfico como linhas vertivais espaçadas, com alturas proporcionais aos coeficiente da componente de frequência correspondente.

No entanto, se formos rigorosos, necessitamos de dois gráficos para representar, completamente, uma funções periódica no domínio de frequência: o espectro e amplitude e o espectro de fase, como podemos melhor perceber na solução da equação da onda unidimensional.

Exercícios Resolvidos sobre Séries de Fourier

• Séries de Fourier | 1ª Lista de Exercícios Resolvidos
• Séries de Fourier | 2ª Lista de Exercícios Resolvidos

Leia Mais:

• Séries de Fourier | Ortogonalidade das Funções Seno e Cosseno
• O Que São Funções Periódicas? Definição e Exemplos.
• Séries de Fourier | Os Coeficientes de Fourier
• Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.

Assista Nossa Vídeo-Aula Sobre Séries de Fourier: