Séries de Fourier | 1ª Lista de Exercícios Resolvidos

Neste artigo apresentamos uma primeira lista de exercícios resolvidos sobre as Séries de Fourier, que são largamente utilizadas na resolução de muitos problemas de valores de contorno. Alguns exemplos clássicos são: 1) fluxo do Calor; 2) equação de Laplace; e 3) os sistemas Vibrantes.

As condições de Dirichlet nos diz que supondo f(x) definida, exceto possivelmente em um número finito de de pontos do intervalo (-L,L), periódica de período 2L, sendo f(x) e f'(x) seccionalmente contínuas em (-L,L), então a série de Fourier $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ com coeficientes dados por $$a_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{n\pi x}{L} \right)} dx} $$ e $$b_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$ converge para f(x) se x é ponto de continuidade; \frac{f(x+0) + f(x-0) }{2} se x é ponto de descontinuidade, sendo f(x+0) o limite de f(x) à direita de x e f(x-0) o limite de f(x) à esquerda de x.

Séries de Fourier | 1ª Lista de Exercícios Resolvidos

1) Esboce o gráfico e encontre as séries de Fourier das funções abaixo. Por fim, utilize o critério de Dirichlet para verificar a convergência da série para a função f(x).

a) f(x) = -x, para -1 \leq x < 1 e f(x+2)=f(x).

Note que esta é uma função ímpar, definida e seccionalmente contínua no intervalo (-1,1), e sua derivada é dada por f(x) = -1  que também é uma função seccionalmente contínua no intervalo (-1, 1) e, ainda, f é periódica de período igual a 2.

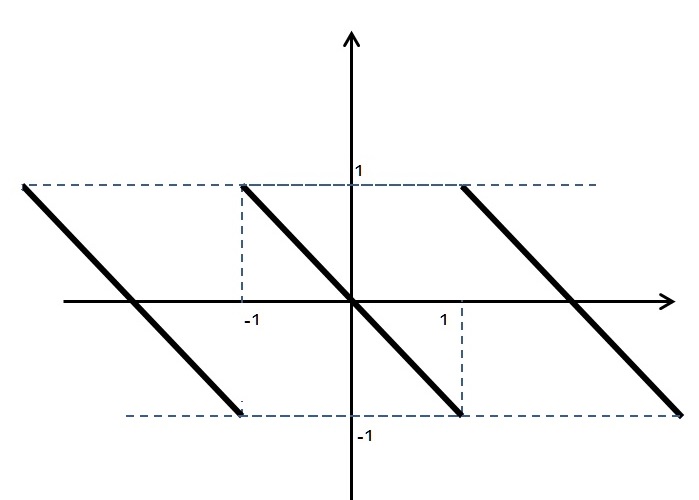
Pelas condições de Dirichilet

$$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$.

Como f(x) é ímpar, então

$$a_0 = a_n = 0$$

e

$$b_n = – \int\limits _{-1}^{1}{ x \sin{\left( \frac{n\pi x}{1} \right)} dx} =
\left\{\begin{array}{cll}
-\frac{1}{n \pi}; & n\;\;\;é\;\;\;par\\
\frac{1}{n \pi}; & n\;\;\;é\;\;\;ímpar\\
\end{array} \right.$$

O que nos leva a

$$ f(x) = \sum\limits_{n=1}^{\infty} \frac{(-1)^{n+1}}{n \pi}  \sin{\left( n \pi x \right)}$$ nos pontos de continuidade de f(x) , e zero nos pontos de descontinuidade.

b) f(x)=\left\{\begin{array}{rl}x; & -\pi \leq x <0\\\\0; & 0 \leq x <\pi \\\\f(x+2\pi) & = f(x)\end{array}\right.

Note que esta função é definida e todos os pontos e seccionalmente contínua no intervalo (-\pi ,\pi) e sua derivada é dada por $$f(x) = \left\{ \begin{array}{rll}
1 & ;& – \pi \leq x <0\\
0 & ;& 0 < x \leq \pi
\end{array} \right.$$ que também é uma função seccionalmente contínua no intervalo (-\pi , \pi ) e ainda, f é periódica de período igual a 2 \pi.

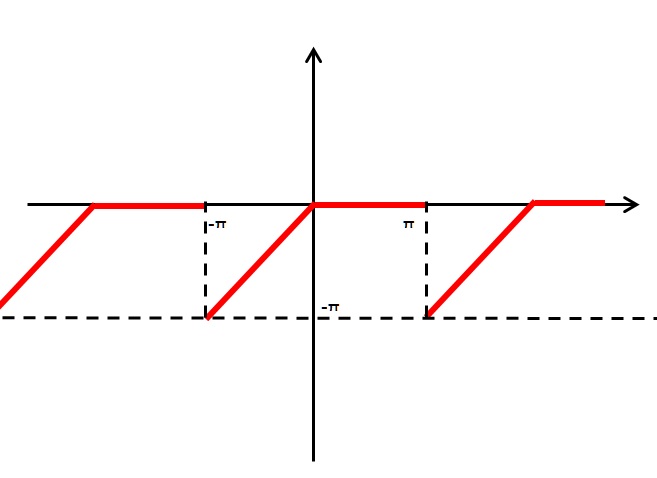
Pelas condições de Dirichilet

$$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ onde

$$a_0 = \frac{1}{\pi} \int\limits _{-\pi}^{\pi}{f(x)dx} = \frac{\pi}{2}$$

$$a_n = \frac{1}{\pi} \int\limits _{-\pi}^{\pi}{ x \cos{\left( \frac{n x}{L} \right)} dx} = \left\{\begin{array}{cll}
\frac{2}{n^2 \pi}; & n\;\;\;é\;\;\;par\\
0; & n\;\;\;é\;\;\;ímpar\\
\end{array} \right.$$

e

$$b_n = \frac{1}{\pi} \int\limits _{-\pi}^{\pi}{ \sin{\left( \frac{n x}{L} \right)} dx} =
\left\{\begin{array}{cll}
\frac{1}{n \pi}; & n\;\;\;é\;\;\;par\\
– \frac{1}{n \pi}; & n\;\;\;é\;\;\;ímpar\\
\end{array} \right.$$

O que nos leva a

$$ f(x) = \frac{\pi}{4} + \sum\limits_{n=1}^{\infty} \left( \frac{(-1)^n sen(n x)}{n \pi} + \frac{cos(2n x)}{2n^2}  \right), $$ nos pontos de continuidade e \frac{- \pi}{2} nos pontos de descontinuidade.

c) f(x)=\left\{\begin{array}{rl}x+1; & -1 \leq x <0\\\\1-x; & 0 \leq x <1 \\\\f(x+2) & = f(x)\end{array}\right.

Note que esta função é seccionalmente contínua no intervalo (-1 ,1) e sua derivada é dada por $$f(x) = \left\{ \begin{array}{rll}
1 & ;& – 1 \leq x <0\\
-1 & ;& 0 < x \leq 1
\end{array} \right.$$ que também é uma função seccionalmente contínua no intervalo (-1 , 1 ) e ainda, f é periódica de período igual a 2.

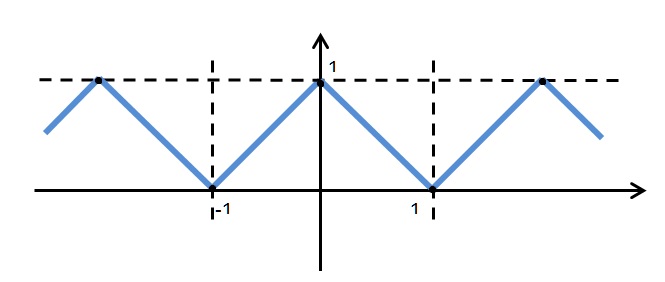
Pelas condições de Dirichilet

$$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ onde

$$a_0 = \int\limits _{-1}^{1}{f(x)dx} = 1$$

Como a função é par, $$b_n = 0$$ e

$$a_n = 2 \int\limits _{0}^{1}{ (1-x) \cos{\left( n \pi x \right)} dx} = \left\{\begin{array}{cll}
\frac{4}{(n \pi)^2}; & n\;\;\;é\;\;\;par\\
0; & n\;\;\;é\;\;\;ímpar\\
\end{array} \right.$$

O que nos leva a

$$ f(x) = \frac{1}{2} + \sum\limits_{n=1}^{\infty}\frac{cos(2n \pi x)}{(n \pi)^2}$$ em todos os seus pontos, pois ela não possui pontos de descontinuidade.

d) f(x)=\left\{\begin{array}{rl}1-x; & 0 \leq x <1\\\\0; & 1 \leq x <2 \\\\f(x+2L) & = f(x)\end{array}\right.

Note que esta função é seccionalmente contínua no intervalo (0 ,2) e sua derivada é dada por $$f(x) = \left\{ \begin{array}{rll}
-1 & ;& – 1 \leq x <0\\
0 & ;& 0 < x \leq 1
\end{array} \right.$$ que também é uma função seccionalmente contínua no intervalo (0 , 2 ) e ainda, f é periódica de período igual a 2.

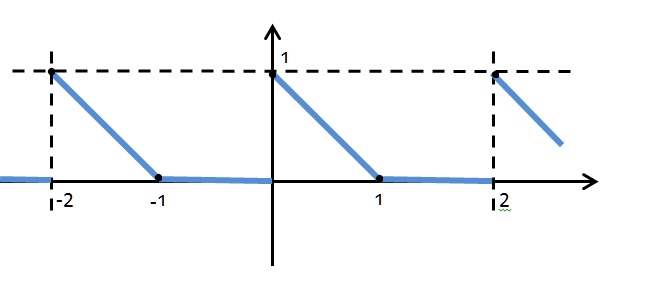
Pelas condições de Dirichilet

$$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ onde

$$a_0 = \int\limits _{0}^{2}{f(x)dx} = \frac{1}{2}$$

$$a_n = \int\limits _{0}^{1}{ (1-x) \cos{\left( n \pi x \right)} dx} = \left\{\begin{array}{cll}
\frac{4}{(n \pi)^2}; & n\;\;\;é\;\;\;par\\
0; & n\;\;\;é\;\;\;ímpar\\
\end{array} \right.$$

$$b_n = \int\limits _{0}^{1}{(1-x ) \sin{\left( n \pi x \right)} dx} = \frac{1}{n \pi}$$

O que nos leva a

$$ f(x) = \frac{1}{4} + \sum\limits_{n=1}^{\infty} \left( \frac{cos(2n \pi x)}{(n \pi)^2}  + \frac{sen(n \pi x)}{n \pi} \right)$$ nos pontos de continuidade e \frac{1}{2} nos pontos de descontinuidade.

2. (Retificador de Meia-Onda) Uma voltagem senoidal E sen( \omega t), onde t é o tempo, percorre um retificador de meia-onda que corta a porção negativa da onda. Encontre a série de Fourier da função periódica que é dada por $$ u(t) = \left\{ \begin{array}{rll}
0 & ; & -L < t < 0 \\
E sen( \omega t) & ; & 0 < t < L
\end{array} \right.$$ onde o período é igual a 2L = \dfrac{2 \pi}{\omega}.

SOLUÇÃO: Como u = 0 quando -L < t < 0 , nós obtemos $$a_0 = \frac{\omega}{2 \pi} \int_{0}^{\pi / \omega}{E sen( \omega t) dt} = \frac{E}{\pi}$$ $$a_n = \frac{\omega}{2 \pi} \int_{0}^{\pi / \omega}{E sen( \omega t) cos(n \omega t)dt} = \frac{E \omega}{2 \pi} \int_{0}^{\pi / \omega}{ [sen((1+n)  \omega t) + sen((1-n) \omega t)]dt} =$$ $$= \frac{E}{2 \pi} \left(  \frac{-cos((1+n) \pi) +1}{1 +n} + \frac{-cos((1-n) \pi) +1}{1 – n} \right).$$ Se n é par, então a_n = 0 , e se n é ímpar, então $$a_n = \frac{E}{2 \pi} \left(  \frac{2}{1 +n} + \frac{2}{1 – n} \right) = – \frac{2E}{(n-1)(n+1) \pi}.$$

De modo análogo, podemos encontrar b_1 = E/2 e b_n = 0 para n=2,3,4,5,... . Consequentemente,

$$u(t) = \frac{E}{\pi} + \frac{E}{2} sen (\omega t ) – \frac{2E}{\pi} \left( \frac{1}{1.3} cos(2 \omega t) +  \frac{1}{3.5} cos(4 \omega t) + \frac{1}{5.7} cos(6 \omega t) +  \frac{1}{7.9} cos(8 \omega t) +… \right) $$

3. (Equação do Calor Unidimensional) Use a Série de Fourier para solucionar a equação do calor unidimensional dada por $$\frac{\partial u}{\partial t} = c^2 \frac{\partial ^2 u}{\partial x^2}$$ com as condições de contorno $$u(0,t) = 0 = u(L,t), \forall t$$ e a condição inicial $$u(x,0) = f(x).$$ (Dica: Use o mesmo raciocínio que usamos para solucionar a equação da onda onda unidimensional)

SOLUÇÃO: Usaremos o Método da Separação das Variáveis para solucionar esse problema. Desta forma, assumindo que a solução é da forma  u(x,t) = F(x) G(t) , o que nos leva à equação $$ F \dot{G} = c^2 F” G$$, o que nos leva a $$\frac{\dot{G}}{c^2 G} = \frac{F”}{F}.$$

Como ambos os lados dependem de apenas uma das variáveis, $$\frac{\dot{G}}{c^2 G} = \frac{F”}{F}=k.$$

Por consequência, encontramos duas equações diferenciais de segunda ordem dadas por

\begin{eqnarray*}
\dot{G}(t) – c^2 k G(t) & = & 0\\
\\
F”(x) – k F(x) & = & 0\\
\end{eqnarray*}

Primeiramente devemos resolver a equação em F .

Se k>0 então a equação característica da equação diferencial é dada por $$\lambda ^2 -k = 0$$ que nos fornece uma solução $$F(x) = A e^{-\sqrt{k}x}+Be^{\sqrt{k}x}.$$

Pelas condições iniciais $$F(0) = A + B = 0 \Leftrightarrow A=-B$$ e $$F(l) = A e^{-\sqrt{k}l}+Be^{\sqrt{k}l} = -B e^{-\sqrt{k}l}+Be^{\sqrt{k}l} = 0 \Leftrightarrow B = 0 \Rightarrow A=0,$$ ou seja, F(x) = 0 se k>0.

Desta forma, devemos ter que k<0. Sendo assim, tomando k = -p^2, obtemos $$F(x) = A \cos{px}+B\sin{px}.$$ Pela condições iniciais,

$$F(0) = A = 0$$ e $$F(L) = B\sin{pl} = 0 \Leftrightarrow pl = n\pi \Leftrightarrow p = \frac{n \pi}{l}.$$

Desta forma, podemos dizer existem infinitas funções dadas por $$F_n (x) = B \sin{\left( \frac{n \pi}{l} x \right)}$$ que satisfazem a equação acima.

Porém, cada solução possui coeficientes B que podem variar de solução para solução.

Portanto, é usual escrever $$F_n (x) = B_n \sin{\left( \frac{n \pi}{L} x \right)}.$$

Já sabemos que $$k = -p^2 = – \left( \frac{n \pi}{l} \right)^2.$$

Assim, $$c^2 k = -\left( c \frac{n \pi}{l} \right)^2 $$ e considerando q = \frac{cn \pi}{l} a equação diferencial dependendo de t é dada por $$\dot{G} – {q_n}^2 G = 0 $$ que tem solução geral dada por $$G_n (t) = C_n e^{-{q_n}^2 t}$$ onde C_n é uma constante.

Desta forma, as funções $$u_n (x,t) = F_n (x) G_n (t) = B_n C_n sen\left( \frac{n \pi x}{L} \right) e^{-{q_n}^2 t}$$ são soluções da equação do calor.

Pelo Teorema da Superposição, obtemos $$u(x,t) = \sum\limits_{n=1}^{\infty}{u_n (x,t)} = \sum\limits_{n=1}^{\infty}{B_n C_n sen\left( \frac{n \pi x}{L} \right) e^{-{q_n}^2 t}}$$

Pela condição inicial temos que $$u(x,0) = \sum\limits_{n=1}^{\infty}{u_n (x,t)} = \sum\limits_{n=1}^{\infty}{B_n C_n sen\left( \frac{n \pi x}{L} \right)} = f(x).$$

Portanto, o coeficiente B_n C_n   deve ser o coeficiente da série de senos de Fourier, que é dado por $$B_n C_n = \frac{2}{L} \int_{0}^{L}{f(x) sen \left( \frac{n \pi x}{L} \right) dx}.$$

Exercícios Resolvidos sobre Séries de Fourier

• Séries de Fourier | 2ª Lista de Exercícios Resolvidos

Leia Mais:

• Séries de Fourier | História, Definição e Condições de Convergência.
• Séries de Fourier | Ortogonalidade das Funções Seno e Cosseno
• O Que São Funções Periódicas? Definição e Exemplos.
• Séries de Fourier | Os Coeficientes de Fourier
• Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.

Assista Nossa Vídeo-Aula Sobre Séries de Fourier: