Como Calcular os Coeficientes de Fourier? | Séries de Fourier

Neste artigo queremos deduzir os coeficientes da Série de Fourier de uma função f(x) .

Advirto que neste artigo supomos que a série de Fourier convirja uniformemente para f(x) em (-L, L), e, por isso, as permutações sentre soma e integração que faremos serão válidas.

Mesmo quando não se faz tal hipótese, os coeficientes obtidos são chamados Coeficientes de Fourier correspondente a f(x) , e a série correspondente é chamada de série de Fourier correspondente a f(x) .

As condições de convergência são estudadas neste artigo.

Deduzindo os Coeficientes de Fourier

Vamos supor que f(x) é uma funções periódica com período 2 L e que pode ser escrita pela série trigonométrica $$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right).$$

Desta forma, é de se supor que que os coeficientes a_n e b_n estejam ligados à função f(x).

Partindo desta suposição, temos que $$f(x) \cos{\left( \frac{m\pi x}{L} \right)} = \frac{1}{2} a_0 \cos{\left( \frac{m\pi x}{L} \right)} +$$  $$+ \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right) \cos{\left( \frac{m\pi x}{L} \right)}=$$

$$= \frac{1}{2} a_0 \cos{\left( \frac{m\pi x}{L} \right)} + $$ $$+\sum\limits_{n=1}^{\infty}{ a_n \cos{\left( \frac{n\pi x}{L} \right)}}\cos{\left( \frac{m\pi x}{L} \right)} + \sum\limits_{n=1}^{\infty}{ b_n \sin{\left( \frac{n\pi x}{L} \right)}} \cos{\left( \frac{m\pi x}{L} \right)}.$$

Observe que se f(x) é uma função que admite integração no intervalo $[-L,L]$, então

\begin{eqnarray*}
\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{m\pi x}{L} \right)} dx} & = & \frac{1}{2}\int\limits _{-L}^{L} a_0 \cos{\left( \frac{m\pi x}{L} \right)}+\sum\limits_{n=1}^{\infty} \int\limits _{-L}^{L}{ a_n \cos{\left( \frac{n\pi x}{L} \right)}\cos{\left( \frac{m\pi x}{L} \right)}dx} +\\
& & + \sum\limits_{n=1}^{\infty} \int\limits _{-L}^{L}{ b_n \sin{\left( \frac{n\pi x}{L} \right)}} \cos{\left( \frac{m\pi x}{L} \right) }dx
\end{eqnarray*}

Como u(x) = \sin{\left( \frac{m \pi}{L} x \right)} e v(x) = \cos{\left( \frac{n \pi}{L} x \right)} são funções ortogonais e pelos resultados obtidos nesse artigo, temos que

$$\sum\limits_{n=1}^{\infty} \int\limits _{-L}^{L}{ b_n \sin{\left( \frac{n\pi x}{L} \right)}} \cos{\left( \frac{m\pi x}{L} \right) }dx = 0,$$ por outro lado $$\int\limits _{-L}^{L}{ a_n \cos{\left( \frac{n\pi x}{L} \right)}\cos{\left( \frac{m\pi x}{L} \right)}dx} \neq 0 \Leftrightarrow m = n.$$  Logo, $$\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{m\pi x}{L} \right)} dx} = \frac{1}{2}\int\limits_{-L}^{L} a_0 \cos{\left( \frac{m\pi x}{L} \right)} + a_m L = a_m L.$$ Portanto, $$a_m = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{m\pi x}{L} \right)} dx}$$

Para encontrar b_n, utilizamos um raciocínio análogo, multiplicando $$f(x) = \frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ por $$\sin{\left( \frac{m\pi x}{L} \right)}.$$
Desta forma, encontramos

$$b_m = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$

A Definição dos Coeficientes de Fourier

Denominados coeficientes de Fourier de f(x) aos termos a_n e b_n dados por $$a_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{n\pi x}{L} \right)} dx} $$ e $$b_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$

Note que por causa da periodicidade dos integrandos, o intervalo de integração para os coeficientes de Fourier podem ser substituidos por qualquer outro intervalo de tamanho 2L, por exemplo, o intervalo [0, 2L].

UM IMPORTANTE CONCEITO DE ANÁLISE REAL:

Note que o cálculo dos coeficientes de Fourrier estão condicionados ao fato da função f(x) ser ou não integrável no intervalo [-L, L].

Para garantir esta integrabilidade basta que f(x) seja seccionalmente contínua no intervalo [-L, L].

Existe uma propriedade interessante quando se fala em integração de funções pares ou ímpares.

Seja f(x) uma função definida num intervalo [-L, L].

1. se f é ímpar, então \int\limits _{-L}^{L}{f(x)dx} = 0.
2.  se f  é par, então \int\limits _{-L}^{L}{f(x)dx} = 2 \int\limits _{0}^{L}{f(x)dx} .

UM EXEMPLO DE COMO CALCULAR OS COEFICIENTES DE FOURIER

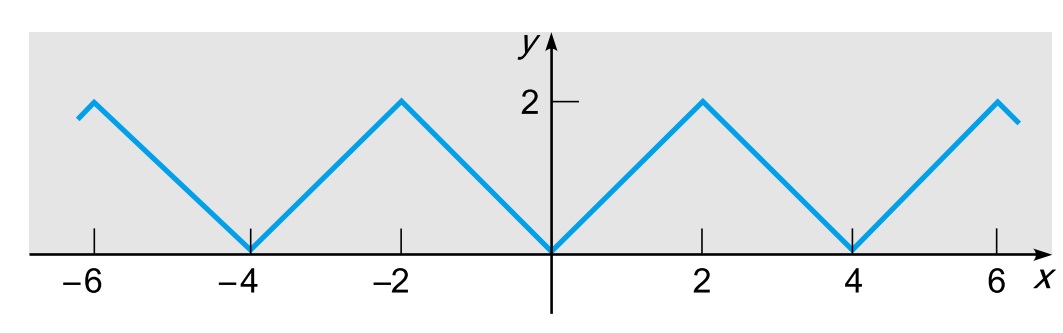
Considere $$f(x) = \left\{ \begin{array}{rll}
-x & , & -2\leq x \leq 0\\
x &, & 0 \leq x \leq 2 \end{array} \right. $$

Esta função representa a onda triangular de altura 2 e base 4 dada pela figura abaixo

Vamos encontrar os coeficientes de Fourrier de f(x).

Note que f(x) é contínua e, por consequência, integrável.

Se n=0 então

$$a_0 = \frac{1}{2}\int\limits _{-2}^{2}{f(x) dx} = 2 \left( \frac{1}{2}\int\limits _{0}^{2}{xdx} \right) = 2$$

Se n>0,

$$a_n = \frac{1}{2}\int\limits _{-2}^{2}{f(x) \cos{\left( \frac{n\pi x}{2} \right)} dx} = \frac{1}{2}\left[ \int\limits _{-2}^{0}{-x \cos{\left( \frac{n\pi x}{2} \right)} dx}+ \int\limits _{0}^{2}{x \cos{\left( \frac{n\pi x}{2} \right)} dx} \right] = $$
$$= \frac{1}{2}\left[ \int\limits _{0}^{2}{x \cos{\left( \frac{n\pi x}{2} \right)} dx}+ \int\limits _{0}^{2}{x \cos{\left( \frac{n\pi x}{2} \right)} dx} \right] = \left[ \frac{x\sin{\left(\frac{n\pi x}{2} \right)}}{\frac{n\pi }{2} } + \frac{\cos{\left(\frac{n\pi x}{2} \right)}}{\left(\frac{n\pi }{2} \right)^2}\right]_{0}^{2}=$$
$$=\frac{\cos{(n \pi)}}{\left(\frac{n\pi }{2} \right)^2} – \frac{1}{\left(\frac{n\pi }{2} \right)^2}= \left\{ \begin{array}{lll}
0&;& n\;\;\;é\;\;\;par\\
\frac{-8}{n^2 \pi ^2} &;& n\;\;\;é\;\;\;ímpar\\ \end{array} \right.$$

Vamos determinar o coeficiente b_n.

$$b_n = \frac{1}{2}\int\limits _{-2}^{2}{f(x) \sin{\left( \frac{n\pi x}{2} \right)} dx} = \frac{1}{2}\left[ \int\limits _{-2}^{0}{-x \sin{\left( \frac{n\pi x}{2} \right)} dx}+ \int\limits _{0}^{2}{x \sin{\left( \frac{n\pi x}{2} \right)} dx} \right] = $$
$$ = – \left[ \frac{- x\cos{\left(\frac{n\pi x}{2} \right)}}{\frac{n\pi }{2} } + \frac{\sin{\left(\frac{n\pi x}{2} \right)}}{\left(\frac{n\pi }{2} \right)^2}\right]_{-2}^{0} + \left[ \frac{- x\cos{\left(\frac{n\pi x}{2} \right)}}{\frac{n\pi }{2} } + \frac{\sin{\left(\frac{n\pi x}{2} \right)}}{\left(\frac{n\pi }{2} \right)^2}\right]_{0}^{2} = $$ $$ \left[ \frac{- 2\cos{\left(-n\pi \right)}}{\frac{n\pi }{2}} \right] + \left[ \frac{ 2\cos{\left(n\pi \right)}}{\frac{n\pi }{2}} \right]= \left[ \frac{- 2\cos{\left(n\pi \right)}}{\frac{n\pi }{2}} \right] + \left[ \frac{ 2\cos{\left(n\pi \right)}}{\frac{n\pi }{2}} \right] = 0$$

Leia Mais:

• Séries de Fourier | Ortogonalidade das Funções Seno e Cosseno
• O Que São Funções Periódicas? Definição e Exemplos.
• Séries de Fourier | História, Definição e Condições de Existência.
• Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.
• Desafios de Matemática: 11 problemas para desafiar sua mente
• Efeito Borboleta | Edward Lorenz e a Teoria do Caos