Séries de Fourier | 2ª Lista de Exercícios Resolvidos

Neste artigo apresentamos uma segunda lista de exercícios resolvidos sobre as Séries de Fourier, que são largamente utilizadas na resolução de muitos problemas de valores de contorno. Alguns exemplos clássicos são: 1) fluxo do Calor; 2) equação de Laplace; e 3) os sistemas Vibrantes.

As condições de Dirichlet nos diz que supondo f(x) definida, exceto possivelmente em um número finito de de pontos do intervalo (-L,L), periódica de período 2L, sendo f(x) e f'(x) seccionalmente contínuas em (-L,L), então a série de Fourier $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ com coeficientes dados por $$a_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{n\pi x}{L} \right)} dx} $$ e $$b_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$ converge para f(x) se x é ponto de continuidade; \frac{f(x+0) + f(x-0) }{2} se x é ponto de descontinuidade, sendo f(x+0) o limite de f(x) à direita de x e f(x-0) o limite de f(x) à esquerda de x.

Séries de Fourier | 1ª Lista de Exercícios Resolvidos

1) Faça o gráfico de cada uma das seguintes funções:

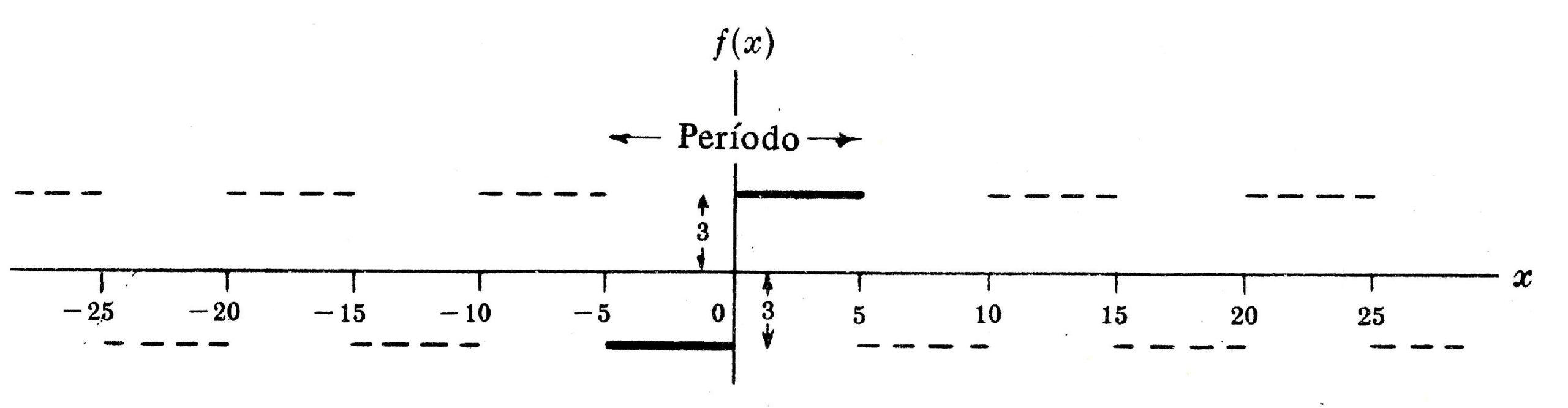
a) f(x) = 3 , se 0 < x < 5 , f(x) = - 3 , se -5 < x < 0 e f(x +10) = f(x).

SOLUÇÃO: Como o período é 10, a porção do gráfico em -5 < x < 5, representa por traço cheio na figura, se repete periodicamente fora desse intervalo (gráfico tracejado). Note-se que f(x) não é definida em x = 0, 5, -5, 10, -10, 15, -15, etc. Esses valores são os pontos de descontinuidade de f(x) .

b) f(x) = sen(x) , se 0 \leq  x \leq \pi , f(x) = 0 , se \pi < x < 2 \pi e f(x + 2 \pi) = f(x).

SOLUÇÃO: Note que f(x) é definida e contínua para todo x .

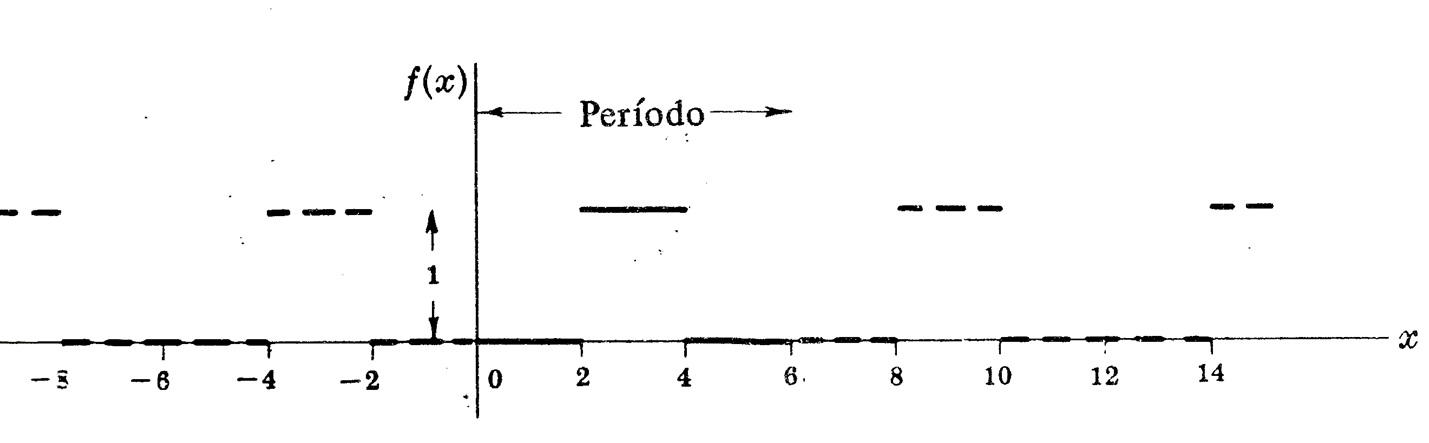
c) f(x) = 0 , se 0 \leq x < 2 , f(x) = 1 , se 2 \leq x < 4 , f(x) = 0 , se 4 \leq x < 6 e f(x +6) = f(x).

SOLUÇÃO:

2) a) Determine os Coeficientes de Fourier correspondentes à função $$f(x)= \left\{\begin{array}{rll} 0 & ; & -5 < x < 0\\ 3 & ; & 0 < x < 5 \\ f(x+10) & = & f(x) \end{array}\right. $$

SOLUÇÃO: Neste caso, temos período igual a 2L=10 e L=5. Desta forma, $$ a_n = \frac{1}{5} \int\limits_{-5}^{5}{f(x) \cos{ \left( \frac{n \pi x}{5} \right) } dx} = \frac{3}{5} \int\limits_{0}^{5}{ \cos{ \left( \frac{n \pi x}{5} \right) } dx} = \frac{3}{5} \left( \frac{5}{n \pi} sen{ \left( \frac{n \pi x}{5} \right) } \right)_{0}^{5} = 0 .$$

$$ a_0 = \frac{3}{5} \int\limits_{0}^{5}{ \cos{ \left( \frac{0 \pi x}{5} \right) } dx} = \frac{3}{5} \int\limits_{0}^{5}{ dx} = 3$$

$$b_n = \frac{1}{5} \int\limits_{-5}^{5}{f(x) sen{ \left( \frac{n \pi x}{5} \right) } dx} = \frac{3}{5}\int\limits_{0}^{5}{sen{ \left( \frac{n \pi x}{5} \right) } dx} = \frac{3}{5} \left( – \frac{5}{n \pi} \cos{ \left( \frac{n \pi x}{5} \right) } \right)_{0}^{5} = \frac{3 (1 – \cos{(n \pi)}}{n \pi} .$$

b) Escreva a série de Fourier correspondente.

SOLUÇÃO: A série de Fourier correspondente é

$$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right) = \frac{3}{2} + \sum\limits_{n=1}^{\infty}\left( \frac{3 (1 – \cos{(n \pi)}}{n \pi} sen{\left( \frac{n\pi x}{5} \right)} \right) = $$ $$ = \frac{3}{2} + \frac{6}{\pi} \left( sen\left( \frac{\pi x}{5} \right) + \frac{1}{3}sen\left( \frac{3\pi x}{5} \right) + \frac{1}{5}sen\left( \frac{5\pi x}{5} \right) + … \right) = $$ $$ = \frac{3}{2} + \frac{6}{\pi} \sum\limits_{n=1}^{\infty}\frac{1}{2n-1} sen \left( \frac{[2n-1] \pi x}{5} \right)$$

c) Como deveríamos definir f(x) em x = -5 , x = 0 e x = 5 a fim de que a série de Fourier convirja para f(x) em - 5 \leq x \leq 5 ?

SOLUÇÃO: Como f(x) satisfaz às condições de Dirichlet, podemos afirmar que  a série converge para f(x) em todos os pontos de continuidades, e para a média aritmética dos limites laterais em cada ponto de descontinuidade.

Em x= -5, 0 e 5 , que são os pontos de descontinuidade, a série converge para \dfrac{3}{2} , como se vê no gráfico abaixo.

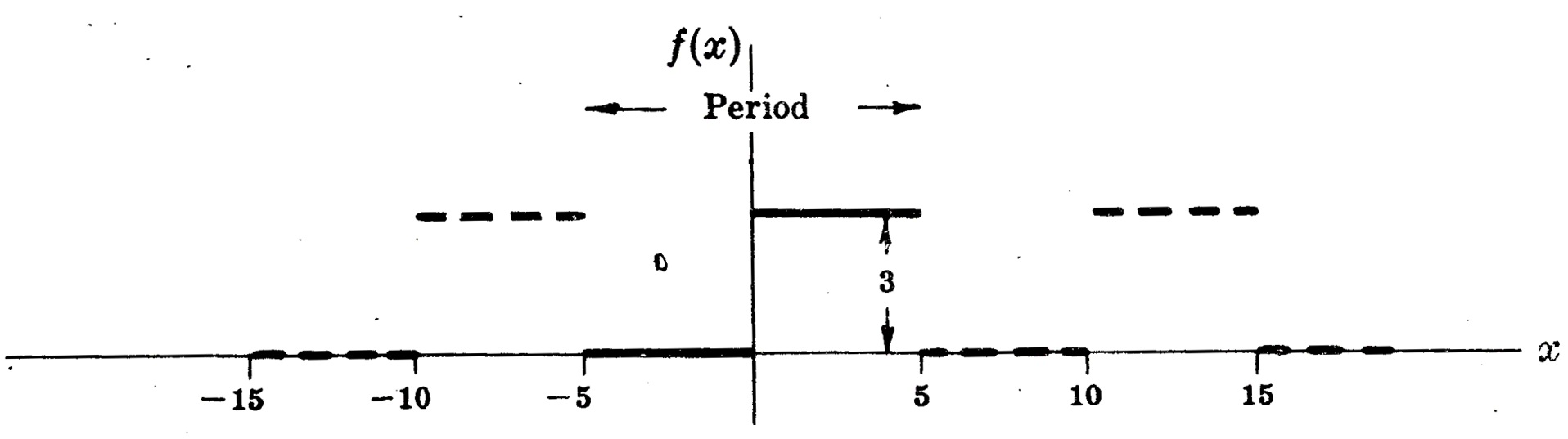
A série convergirá para f(x) em -5 \leq x \leq 5 se redefinirmos f(x) como segue:

$$f(x)= \left\{\begin{array}{rll} 3/2 & ; & x = -5\\ 0 & ; & -5 < x < 0 \\ 3/2 & ; & x = 0 \\ 3 & ; & 0 < x < 5 \\ 3/2 & ; & x = 5 \\ f(x+10) & = & f(x) \end{array}\right. $$

3) Desenvolva f(x) = x^2, 0 < x < 2 \pi , em série de Fourier, se o período é 2 \pi . Use o resultado para provar que $$ \sum\limits_{n = 1}^{\infty}{\frac{1}{n^2}} = \frac{\pi ^2}{6} .$$

SOLUÇÃO: Neste caso, o período 2 L = 2 \pi e L = \pi , como podemos ver no gráfico abaixo:

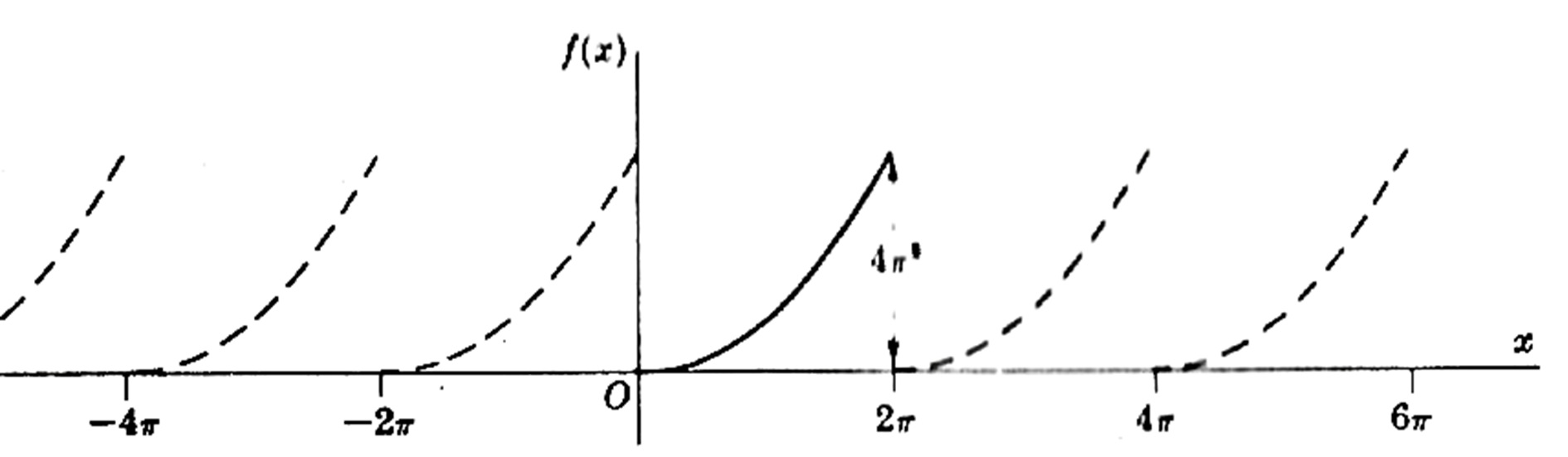
Desta forma, temos $$ a_0 = \frac{1}{\pi}\int\limits_{0}^{2 \pi}{x^2 dx} = \frac{8 \pi ^2}{3}; $$

$$ a_n = \frac{1}{\pi}\int\limits_{0}^{2 \pi}{x^2 \cos{(n x)}} = \frac{1}{\pi} \left[ x^2 \left( \frac{sen(n x)}{n} \right) – 2x \left( – \frac{cos(n x)}{n^2} \right)   + 2 \left( – \frac{sen(n x)}{n^3} \right)  \right]_{0}^{2 \pi} = \frac{4}{n^2}; $$

$$ b_n = \frac{1}{\pi}\int\limits_{0}^{2 \pi}{x^2 sen (nx) dx} =  \frac{1}{\pi} \left[ x^2 \left( – \frac{cos(n x)}{n} \right) – 2x \left( – \frac{sen(n x)}{n^2} \right)   + 2 \left( \frac{cos(n x)}{n^3} \right)  \right]_{0}^{2 \pi} = – \frac{4 \pi}{n} .$$

Então, $$f(x) = x^2 = \frac{4 \pi ^2}{3} + \sum\limits_{n=1}^{\infty}\left( \frac{4}{n^2} \cos{\left(n x \right)}  –  \frac{4 \pi}{n}sen{\left(nx \right)} \right)$$ para 0 < x < 2 \pi .

Agora, para provar que \sum\limits_{n = 1}^{\infty}{\dfrac{1}{n^2}} = \dfrac{\pi ^2}{6} , observamos que em x = 0 a série de Fourier de x^2 se reduz a $$ \frac{4 \pi ^2}{3} + \sum\limits_{n=1}^{\infty}{\frac{4}{n^2}}. $$

Porém, pelas condições de Dirichlet, esta série converge em x = 0 para a média dos limites laterais de f(x) em x = 0, que é dado por $$ \frac{1}{2}(0+4 \pi ^2 ) = 2 \pi ^2,$$ ou seja, $$ \frac{4 \pi ^2}{3} + \sum\limits_{n=1}^{\infty}{\frac{4}{n^2}} = 2 \pi ^2 $$ $$ 4 \sum\limits_{n=1}^{\infty}{\frac{1}{n^2}} = 2 \pi ^2 – \frac{4 \pi ^2}{3} = \frac{2 \pi ^2}{3} $$

$$ \sum\limits_{n=1}^{\infty}{\frac{1}{n^2}} = \frac{ \pi ^2}{6} ,$$ como queríamos demonstrar.

Exercícios Resolvidos sobre Séries de Fourier

• Séries de Fourier | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• Séries de Fourier | História, Definição e Condições de Convergência.
• Séries de Fourier | Ortogonalidade das Funções Seno e Cosseno
• O Que São Funções Periódicas? Definição e Exemplos.
• Séries de Fourier | Os Coeficientes de Fourier
• Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.

Assista Nossa Vídeo-Aula Sobre Séries de Fourier: